Table of Contents
Metallurgists Need Statistics like Pharmaceutical Researchers need Chemistry. See, pharmaceutical manufacturers conduct clinical trials in which new medicines are tested on volunteers to evaluate efficacy and safety. These trials are conducted according to strict statistical protocols that are internationally mandated by government regulation. Why? Because experience has shown that statistically designed trials give the best bang for the considerable buck spent on them, in terms of getting the right answer in an ethical way at acceptable cost.
You might be surprised to learn that pharmaceutical manufacturing and mineral processing have much in common. Both turn raw materials into value-added products, both use sophisticated particle technologies, and both have uncertainties that have to be managed. However, there is one big difference: in testing new medicines rigorous statistical methods are ingrained in the industry’s DNA, whereas in mineral processing we are still more likely to use statistics as an exotic last resort when all else has failed. Metallurgists need computing skills!
This leads to disasters such as that illustrated in Figure 1, which shows the results of a plant trial of a new flotation reagent that appeared to deliver an astonishing increase in gold recovery of over seven percent. The magnitude of the improvement is itself cause for suspicion, and the simple plot of Figure 1 shows why: the recovery was increasing anyway before the switch to the new reagent (probably due to ore changes). One could even conclude that the new reagent has interrupted this improvement. The original conclusion was therefore wrong because with this experimental ‘design’, it was not possible to separate the effects of the reagent from other interfering factors (eg ore type).
If a clinical trial was conducted this way, the organisers would probably end up in jail. But not in mining! Thanks to over engineering.
These sorts of problems are, in fact, quite common. Figure 2 shows a plot of copper recovery versus feed grade in a concentrator in which the trial of a new flotation reagent had been conducted in a haphazard way, running the new and old reagents for a few days at a time with no real plan other than to accumulate data over a period of several months. When everyone’s patience had run out, someone had the job of analysing the data and after some thought did a two-sample t-test to determine the significance of the difference in mean recovery between the two reagents, which was a bit under one percent. The confidence level didn’t quite reach the traditional hurdle rate of 95 per cent, but was close enough to suggest there was evidence for the efficacy of the new reagent; however, a glance at Figure 2 shows that the results when using the new reagent tend to cluster at high feed grades and those using the low reagent at low feed grades. Because of the well-known correlation between recovery and feed grade (apparent in Figure 2), the recovery with the new reagent was indeed higher on average than that with the old, but this had nothing to do with the reagent. It was driven entirely by the prevailing feed grade, essentially a random variable. You might regard this as bad luck, but as in much of life, we make our own luck.
In mineral processing we are still more likely to use statistics as an exotic last resort when all else has failed.
We should be under no illusions as to the negative effect of these kinds of fiascos on the ultimate measure of mining company performance: shareholder value. It leads to wasted expenditure and bad investment decisions.
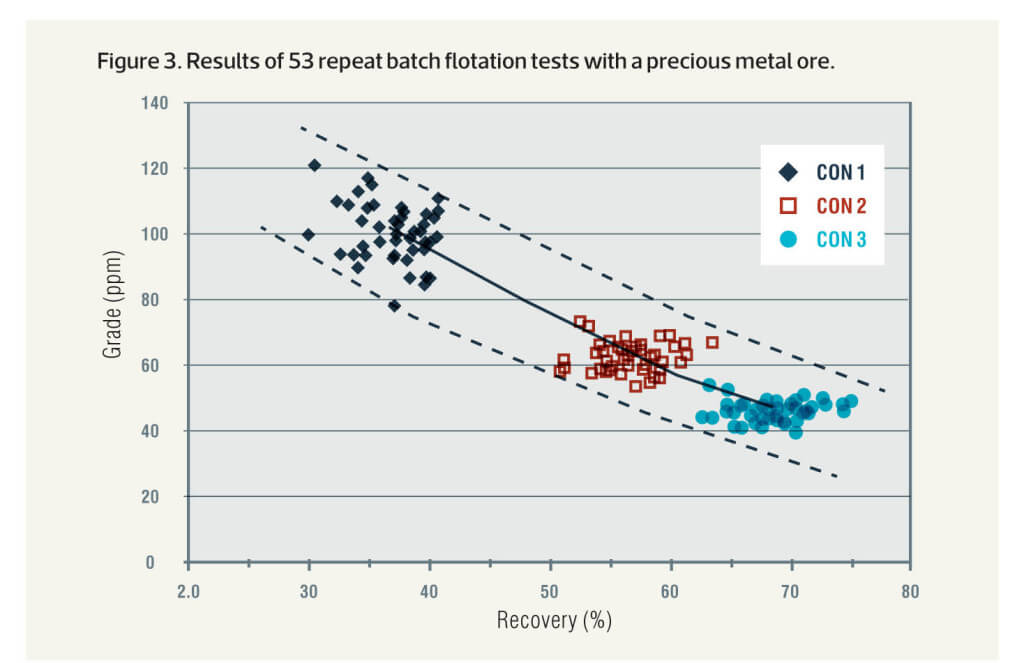
Our difficulties flow from all data carrying uncertainty. Figure 3 shows grade-recovery points for 53 repeat batch flotation tests conducted by a single experienced technician on a precious metal ore under constant conditions. The solid line is drawn between the means of the three concentrate times. The dotted lines show a notional zone of uncertainty for the data. In a perfect world, of course, all the points would fall on a single line.
The scattergraph shows rather dramatically the impact of experimental error on the results, which is quite normal for these kinds of batch flotation experiments. It flows from inevitable errors in sampling, assaying, the conduct of the experiment and so on. And the same principles apply to full-scale plant trials, even more so as the data collection environment is much less benign than it is in the laboratory. How do we deal with the consequent uncertainty in the results?
The solution
The solution to these kinds of problems is to lay out the experiment in such a way that the interfering effects of factors such as feed conditions – which generally can’t be controlled – are separately accounted for or neutralised, leaving the factors we are interested in (reagent in the case studies of Figures 1 and 2) to tell their story unencumbered by process noise. In other words, we should ‘design’ the experiment properly. This is not hard. The solutions to these problems are, in fact, well known; the first book on experimental design was published in 1925 by the great English statistician R A Fisher (you can visit him in St Peter’s Cathedral in Adelaide where his ashes are interred). And in most cases, these solutions are relatively easy to implement in practice. The appropriate data analysis then follows from the chosen design.
A good example of how uncertainty can be quantified and inserted into the process of making informed investment decisions arose in a case some years ago, in which a new piece of equipment was trialled in a particular concentrator. The object was to determine whether there was an economic case for adopting this technology in several of the company’s concentrators, an investment decision worth over US$100 M at the time. A well-designed trial allowed the following statement to be made in the report: ‘We are 95 per cent confident that the improvement in metal recovery at grade using the new equipment is at least 2 per cent’.
Think about what this very powerful statement means. We can attach a low risk (for example, five percent, a one-in-20 chance of being wrong – remember the risk can never be zero) to a specific performance criterion – a minimum of two per cent improvement. It quantifies the worst-case scenario with a known risk of being wrong. If the worst-case scenario meets the company’s normal investment criteria, then in a sense it’s a no-brainer; it is difficult to understand why the company would not make such an investment (everything being equal, of course). A well-designed and analysed trial helps to manage the risk of making a substantial capital investment or moving to a new operating condition. Mining companies are mostly good at understanding risk – it’s a risky business – so such statements should slot in comfortably to their risk management protocols.
It is time that we made properly designed and analysed experiments part of the scenery, as those running clinical trials do. And indeed, as psychologists, economists, production engineers, health scientists and nearly all other numerate professions do. This is regardless of whether the experiment is conducted in a lab, pilot plant or production plant.
The benefits of doing properly designed experiments are twofold:
- They are efficient in that they give the right answer in the minimum number
of tests (read ‘cost-efficient’), and the number of tests required can be calculated before starting. - Analysing the data correctly allows one to explicitly calculate the uncertainty in the conclusion, and thus the risk of being wrong in making a particular decision.
Doing plant trials correctly so that nuisance effects are properly accounted for is easier, cheaper and much more
likely to lead to the right conclusion. And analysing the data from properly designed trials is not hard. So why wouldn’t we use the right methods? Because the teaching of statistics in universities is flawed, and as a result there is an ignorance of these methods in the profession that needs fixing.
I know this because I have spent many years teaching statistics as a professional development course to site-based metallurgists who, when invited to unburden themselves in a preliminary session of ‘Statisticians Anonymous’, freely admit their ignorance. Further empirical evidence is available in the cavalier fashion in which the profession sometimes treats its data, and in the lack of statistical skill that postgraduate students in mineral engineering demonstrate as they take on the challenge of designing experiments and collecting and interpreting data for their thesis.
This unsatisfactory state of affairs is surprising because it turns out that these innocents are numerate, and most have completed (and even passed) a course in statistics at university or technical college. So why this dichotomy, and why is it important?
A well-designed and analysed trial helps to manage the risk of making a substantial capital investment or moving to a new operating condition.
Statistics is a powerful body of methodology that allows wise decisions to be made in the face of uncertainty. It is in a very real sense ‘risk analysis’, as it assigns an explicit risk (a probability) of being wrong in making a particular decision based on imperfect data (ie all metallurgical data). For this reason it is not an optional skill for a metallurgists, it is essential. That is why it is taught to engineers at university.
The problem is that the teaching is usually delivered as a service course by the Maths Department in first year. As the lecturers have the unenviable job of teaching this essential skill to students with interests as diverse as psychology, marine biology and engineering, it is difficult to teach the subject in context, which I (and many others) have found is the key to absorbing the sometimes unintuitive ideas that make the discipline so powerful. This is not the fault of the mathematicians, for whom I have a great respect. And the teaching of statistics to non-statisticians has always been problematic and a well-known challenge. But it is generally still possible to pass the Engineering Stats 101 exam without actually making the connection between the methodology and the needs of our profession, with the unhelpful consequences that we see around us today. We simply ignore the data uncertainties, rather than embrace and manage them.
The best time to teach undergraduate engineers statistics is in the latter years of the course when the context has become clearer. It can be done in association with an honours research project, so that good experimental design practice can be built into the project and the student can see the value first hand. My colleague, Professor Emmy Manlapig, has done this at the University of Queensland with some success. Further skills should be then acquired through continuing professional development in the early stages of a metallurgy career when confronted by the challenges of doing real laboratory experiments and plant trials. Continuing professional development is, in any case, essential – not optional – in an era of lean staffing and increased technical challenges (Drinkwater and Napier-Munn, 2014).
It is also worth pointing out that the ‘fly-in fly-out’ (FIFO) phenomenon is entirely unhelpful to running properly designed plant trials because it makes it hard to achieve the continuity of commitment and project management required. However, this is a matter of organisation – if we think it is important enough, we can plan accordingly.
These arguments apply just as much to experiments done in feasibility studies (ore testing to determine project value or net present value (NPV)) as to those done to try and optimise the performance of existing plant. It is well established that the destruction of NPV caused by failing to reach nameplate capacity in time is often due to inadequate evaluation of the metallurgical properties of the orebody (Mackey and Nesset, 2003). Properly conducted experiments to achieve improved orebody knowledge is part of the solution to this festering problem. (Some might call it ‘geometallurgy’, but ‘orebody knowledge’ is probably a better term).
All is not gloom and doom. I have detected definite improvements in my profession’s attitude to experimental design in recent years. The old guard of technical managers who either never knew any stats or had forgotten what they learned, and who used to tell me proudly that ‘We don’t do it that way here’ are moving on, leaving the job to the smart young guns who are much more receptive to these ideas. And I acknowledge with gratitude the honourable exceptions who have played an important role in encouraging good experimental practice and drawing attention to its benefits. But there is still more to do.
Conclusion
No self-respecting mining company these days would plan and operate a mine without a block model of the deposit developed using geostatistical methods, a sophisticated process managed very effectively by geologists and mining engineers. It’s time we metallurgists followed the same rigorous practices in our own work. It is not hard to do, especially for numerate Excel-drivers, which metallurgists are. Failure to do so leads to expensive trials that either lead to the wrong conclusion or take too long or both. This has a negative impact on shareholder value.
Because of the importance of these issues, we need to do more than just plead for people to do the right thing. Doing tasks the right way should be compulsory, not optional. When faced with similar issues, the geological community developed the JORC Code to ensure
that grades and other important data were properly collected, assessed and presented to the investment community, enabling investment decisions to be properly informed. This has been a very successful innovation. A similar problem exists in metallurgical accounting. My colleague, Dr Rob Morrison, ran an AMIRA research project some years go to develop a code of practice to ensure that metallurgical accounting is done according to proper statistical, sampling and analytical protocols, and edited a how-to book on the subject (Morrison, 2008).
We need to do the same for running metallurgical experiments and plant trials. There should be agreed protocols appropriate to the objectives established at the outset, as is the case in clinical trials. The benefits would be significant: getting a better bang for our buck in doing the experiments in the first place, and improving our decision-making by properly evaluating the risk – an inevitable consequence of the uncertainties in the data. The AusIMM might wish to run a similar process to that which led to the JORC Code. Mining companies, materials and reagent suppliers, equipment vendors and researchers should all be involved in the debate.
Because Metallurgists Need Statistics, we need to take the following action:
- Make sure that all metallurgists are equipped with a basic statistics toolbox through instruction in the final years of undergraduate mineral engineering courses and continuing professional development.
- Mandate appropriate statistical designs and data analysis for plant trials and other key experiments through a JORC-type protocol.
Implementing these suggestions would enrich those mining companies in which my super fund has foolishly invested, and stop my wife from telling me that we do lousy experiments.
Some parts of this article first appeared in HRL Testing’s newsletter in April 2014. Tim Napier-Munn’s book Statistical Methods for Mineral Engineers – How to Design Experiments and Analyse Data is published by the JKMRC (details are on the JKMRC website).