Table of Contents
Desulfurization of coal before combustion is becoming important for the effective utilization of this major energy resource without polluting the environment. Because most sulfur-bearing and ash-forming minerals are finely disseminated in the coal matrix, raw coal must be ground to a fine size in order to liberate and remove them from coal to an acceptable level. Froth flotation is considered to be one of the effective physical cleaning technologies available to separate fine mineral particles from coal. Traditionally, the effectiveness of coal flotation has been evaluated based on yield and product ash and sulfur. However, understanding the flotation kinetic behavior of coal, ash and pyrite is important in order to simulate and optimize flotation separation processes.
Materials and Methods
All coal samples were first crushed to minus ¼ inch and then split into 500-gram subsamples and stored in plastic bags under inert
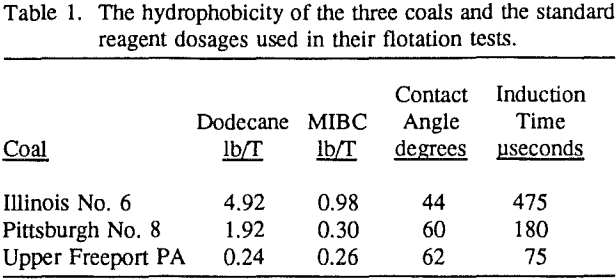
environment. Before flotation, the 500-gram sample was wet ground to 95% passing the desired topsize (28, 100 or 200-mesh) in a rod mill (9 inches in diameter and 10 inches in length) and then split into four parts. Flotation tests were conducted in a 2-liter Denver cell using 125 grams of coal in a pulp at 6.25% solids content at the natural pH (pH 4.5 ± 0.5 for Illinois No. 6 and pH 3.5 ± 0.3 for both Upper Freeport PA and Pittsburgh No. 8 coals) of each coal.
Results and Discussion
In order to evaluate the flotation kinetic parameters for coal flotation, a suitable model must be chosen. Numerous flotation kinetic models have been described in the literature and the selection of an appropriate model for a particular flotation system depends not only on the overall fit of the model to the observed data but also on the statistical significance region of each model parameter. The first-order flotation kinetic model with rectangle distribution of flotabilities were found by Dowling et al. to be suitable for sulfide flotation.
In this investigation, eight flotation kinetic models with two fitting parameters were each tested. The first model is the classical first-order flotation kinetic model:
![]()
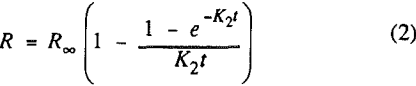
where R = recovery of component at time t
R∞ = ultimate recovery of component
K1 and K2 = first-order rate constants (min-¹).
The third model is the first-order flotation kinetic model with a sine function (in the range of 0 to π/2) distribution of notabilities. The reason for proposing this distribution is that in coal flotation, most of the material in the cell is the flotable component.
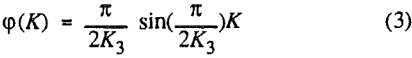
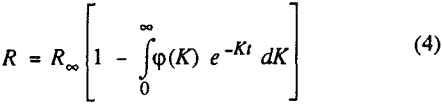
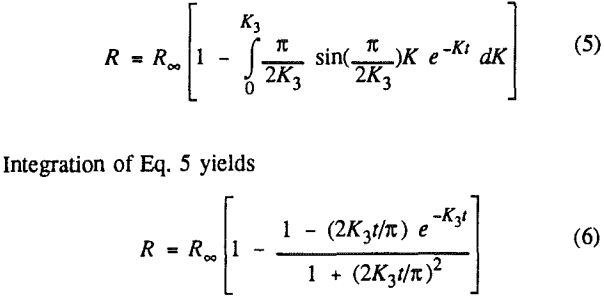
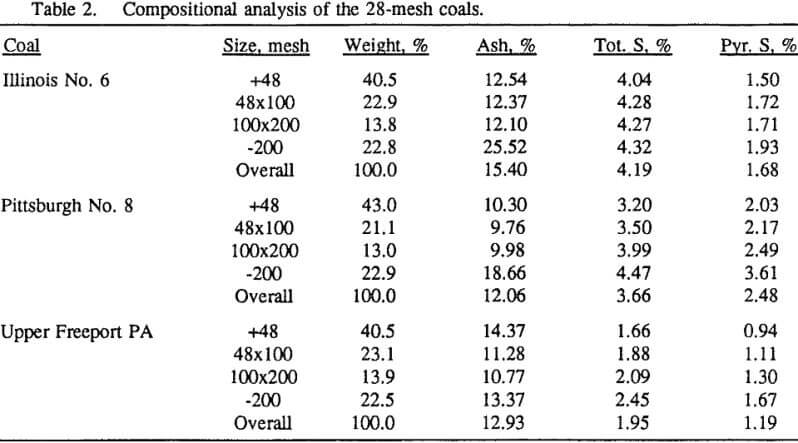
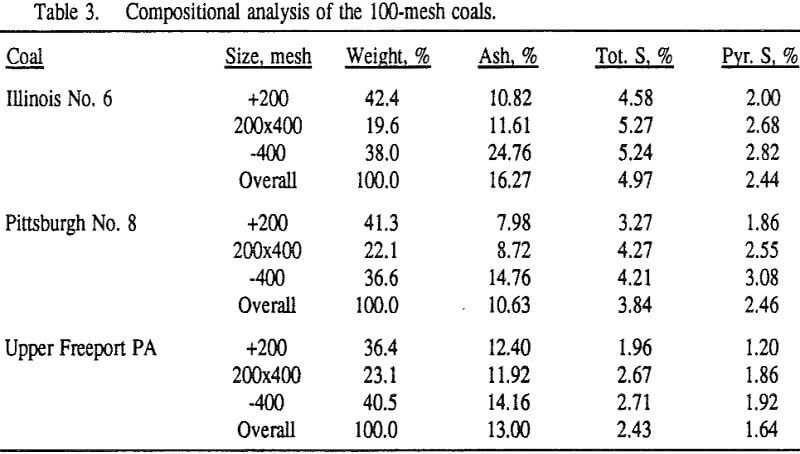
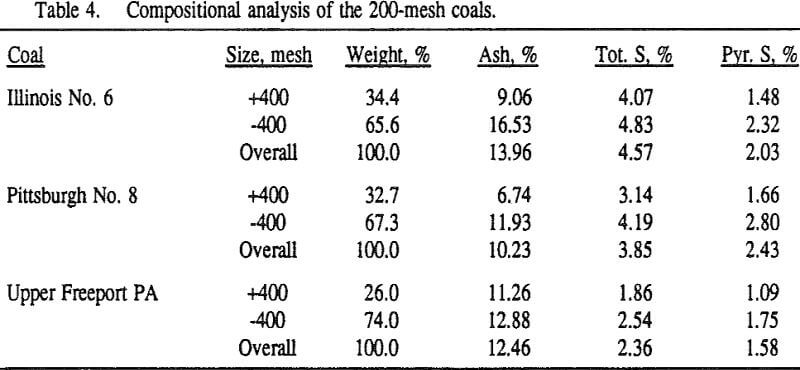
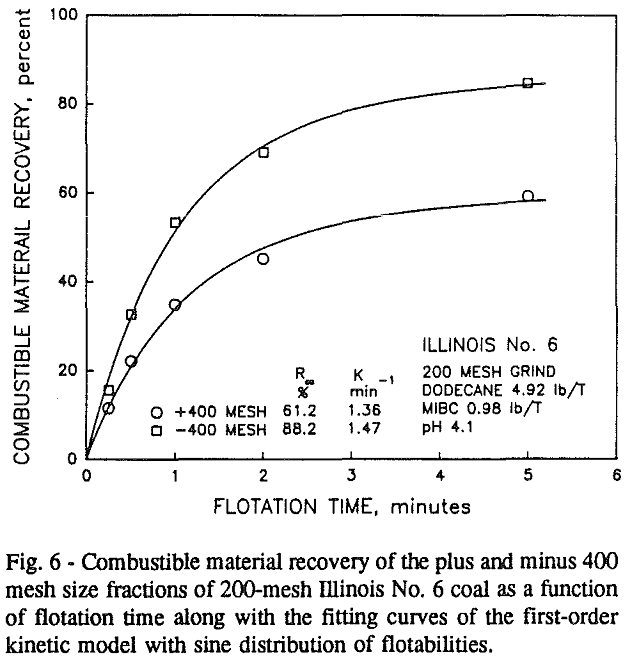
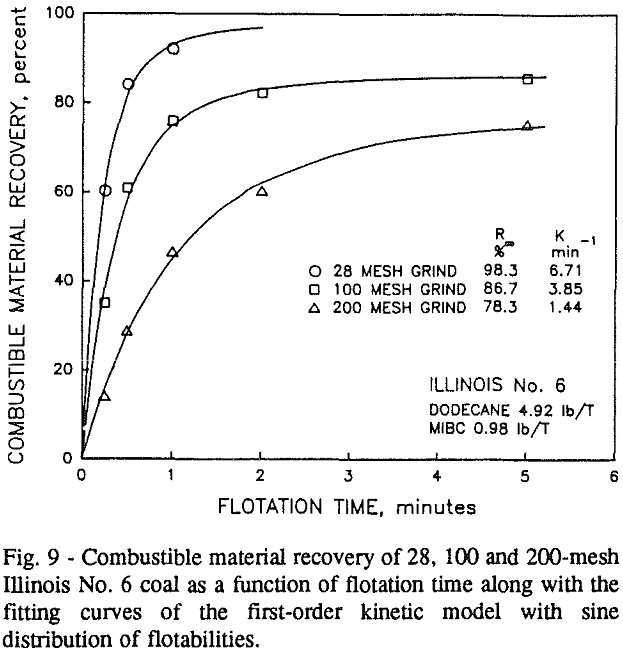
In order to evaluate the suitability of the various models on the flotation time/recovery profiles of the three coals, the results for flotation of the 100 and 200-mesh wet ground coals were used. In particular, the various kinetic parameters were determined for the combustible material recovery in the plus 200, 200 x 400, and minus 400-mesh size fractions and the overall combustible material recovery in the flotation of both the 100-mesh and 200-mesh coal. This comparison of the models showed that the first three can predict flotation behavior quite well. The fourth did as well except that the equation used to describe the model is not valid at times equal to zero. The remaining four models all resulted in standard errors that were much higher than for the first three. Therefore, only the first three models were compared in detail in this work.
Effect of Particle Size on the Flotation
It can be seen from these plots that for all three coals the intermediate size fractions (48×100 and 100×200 mesh) exhibit a maximum in combustible material.
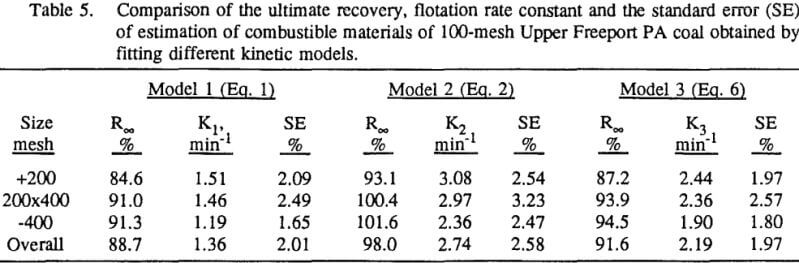
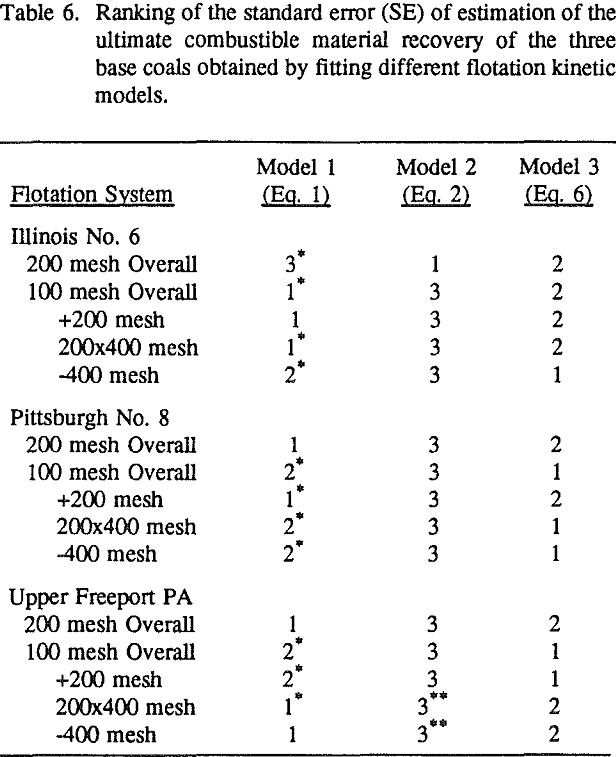
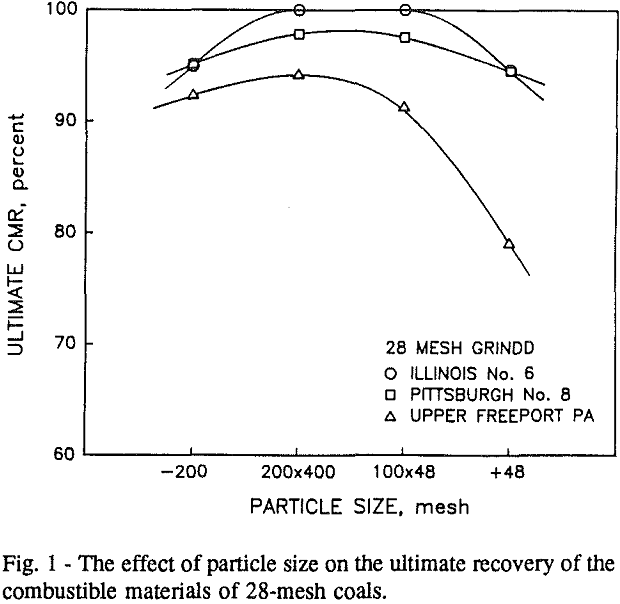
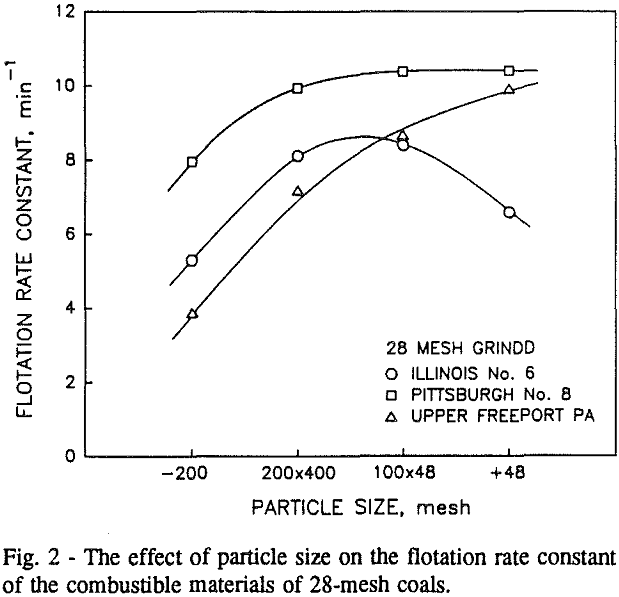
Effect of Particle Size at a 100-mesh Grind
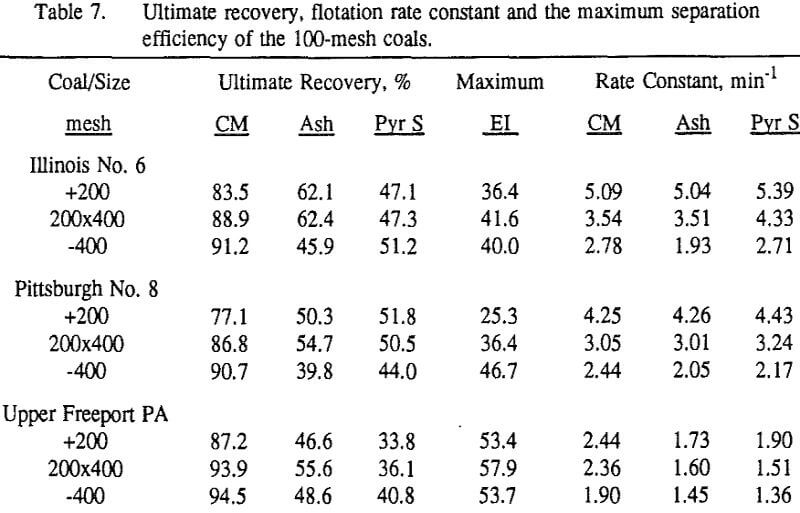
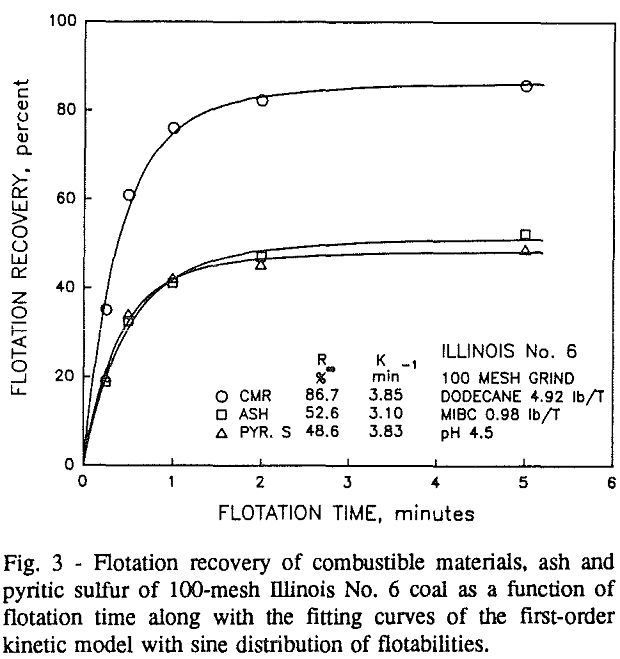
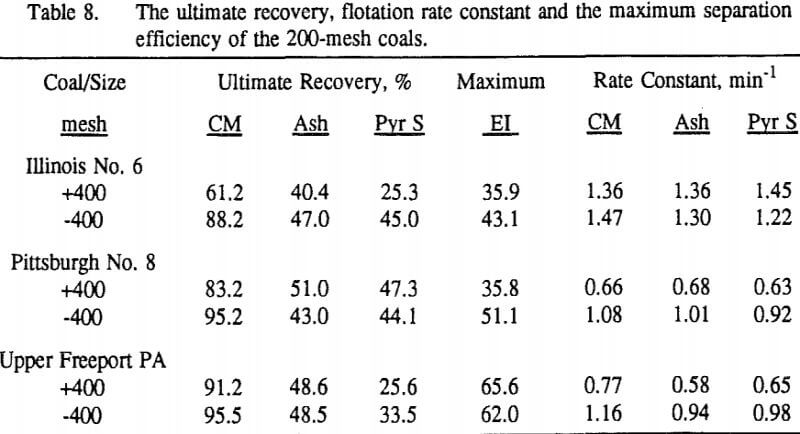
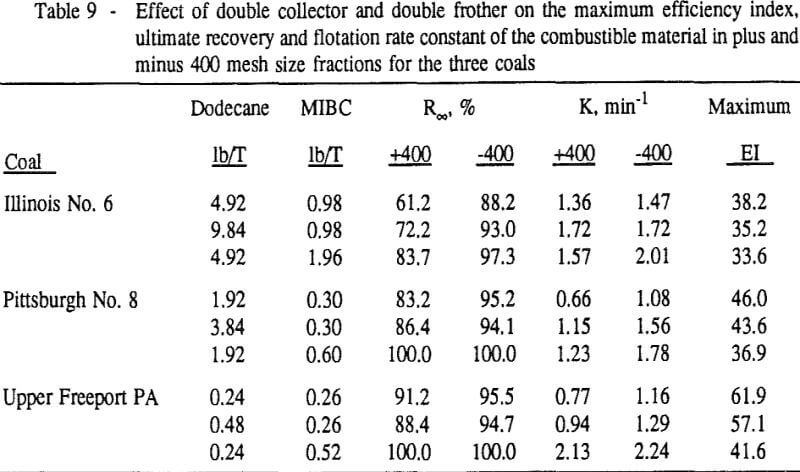
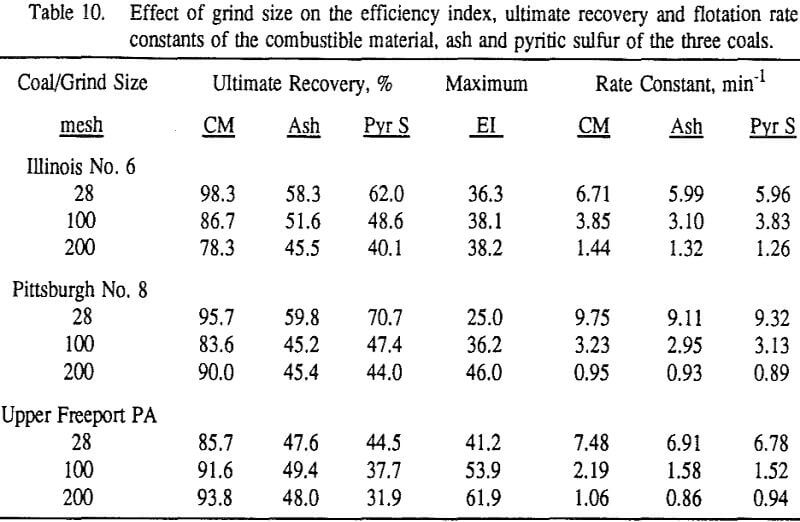
These results show that for all three coals, the ultimate combustible material recovery is significantly higher than that of ash and pyritic sulfur, whereas the flotation rate constant of the combustible material is only slightly higher than that of ash and pyrite. This may indicate that ash and pyrite may be either locked with the coal matrix or carried over by coal particles during flotation.
In general, for a given coal, better liberation in the fine size feeds can lead to decreases in pyritic sulfur recovery. On the other hand, fine pyrite particles are easily carried over by the froth, which then results in an increase in the pyritic sulfur recovery.
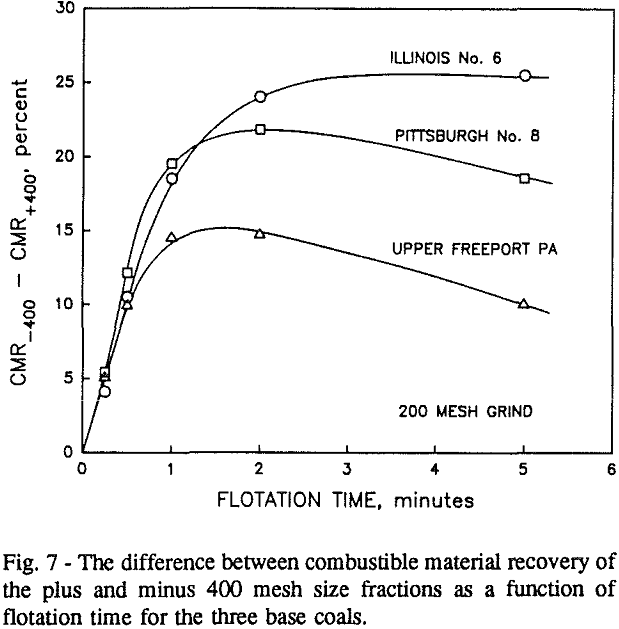
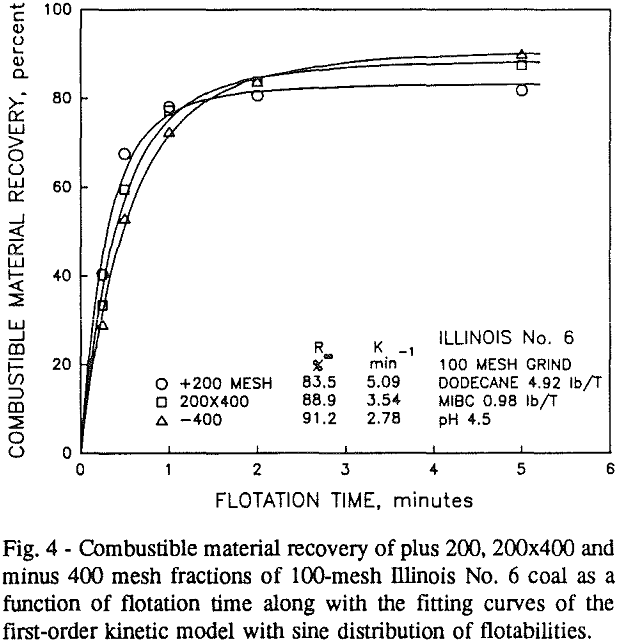
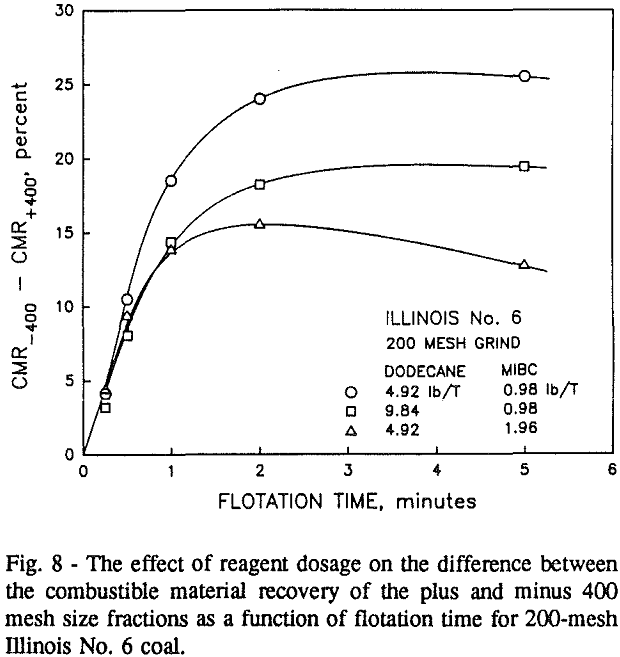
In addition, the rate constant of the fine particles will be enhanced because most of the collector will coat the finer particles and these oil-coated particles tend to form agglomerates. This phenomenon is shown clearly in flotation response of the minus 200-mesh Pittsburgh No. 8 and Upper Freeport PA coals.
Summary and Conclusions
Flotation kinetic behavior of coal can be described by a first-order flotation kinetic model with a sine function (in the range of 0 to π/2) distribution of flotabilities in the flotable particles. The ultimate recovery and flotation rate constant obtained by fitting experimental results with this kinetic model represent the equilibrium recovery of coal and the rate at which this equilibrium state can be reached, respectively.

