The accepted basis of comparisons between mills of different diameter is the percentage critical speed.
If n = actual mill speed, rpm,
nc = calculated critical speed, rpm,
np = calculated percentage critical speed, and
D = inside diameter of the mill in feet,
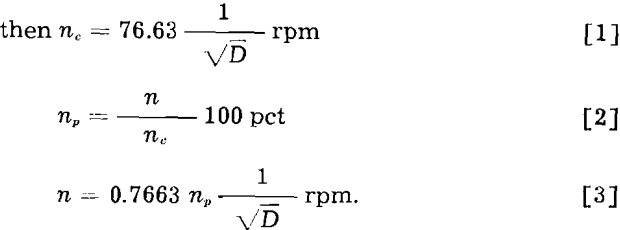
In the following analysis capacity, T, is expressed in short tons per hour, tph, and power consumption, P, in kilowatts, kw. Accordingly power consumption per unit of capacity, Po will be expressed in kilowatt hours per short ton, or kw-hr per ton. In all equations D refers to the inside diameter of the mill in feet and v to the peripheral speed of the mill in feet per minute inside the liners.
It is the general belief that the capacity, T, of a tumbling mill is directly proportional to the speed of the mill, other things remaining constant. Mathematically this is represented by the equation
![]()
where c1, is a factor related with the grinding characteristics of the ore, method of reduction, and the units chosen.
![]()
In other words, the capacity should be proportional to the mill speed raised to power m, the numerical value of the exponent being 1 ≤ m ≤ 1.5, depending on the circumstances. Eq. 5 can also be written in the following forms:
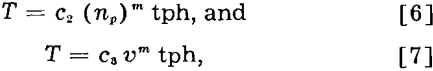
where v = peripheral speed of the mill in feet per minute.
If the observed capacity of a mill at speed n1 is = T1 tph, the capacity T2 of the same mill at speed n2 should be
![]()
![]()
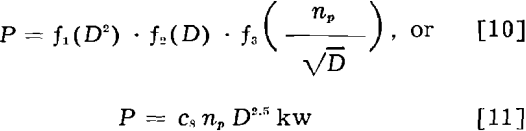
The acceleration factor of the ball or rod mass is a function of the peripheral speed of the mill. Thus
P = f4(F) = f1(D²)·f5(υ)
Indicating that υ = πDn, and
n = c9np/√D, the above equation becomes P = f1(D²)·f5(πD c9 np/√D) = cs np D2.5.
As a first approximation, the capacity, T, of a mill may be considered as a function of the force acting inside the mill. Therefore
T = f6(F) = f1(D²)·f7(υ) tph…………………………………………………..(12)
![]()
Indicating again that υ = πDn, and n = c9np/√D, Eq. 13 becomes
![]()
which is the proposed basic equation relating capacity, mill diameter, and speed. If m = 1.0, Eq. 14 becomes
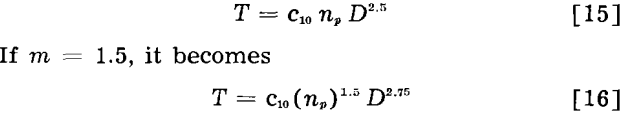
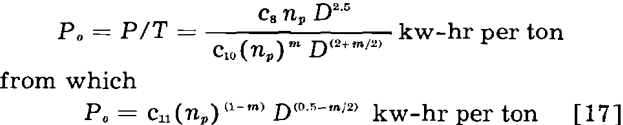
The cornerstone of the mathematical treatment presented is the relationship between mill capacity and speed as expressed in Eq. 5.
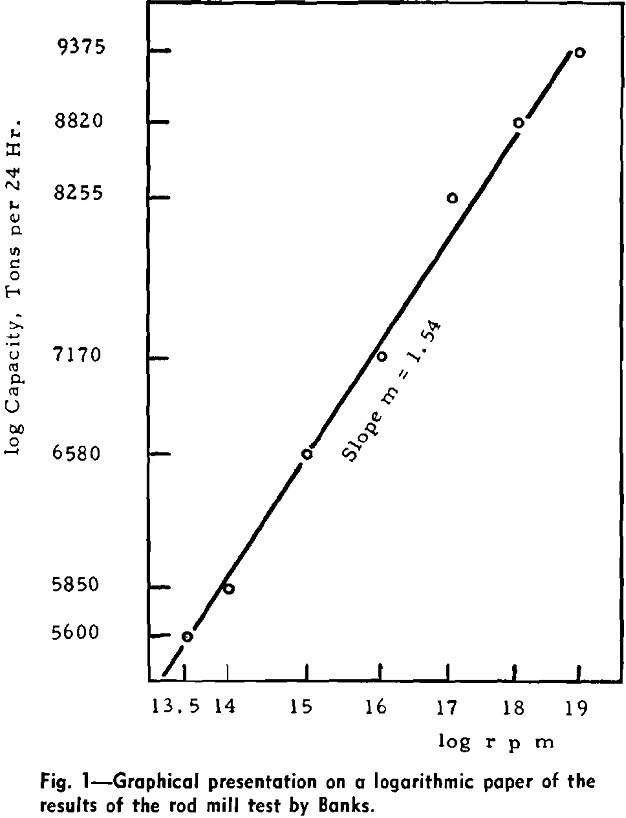
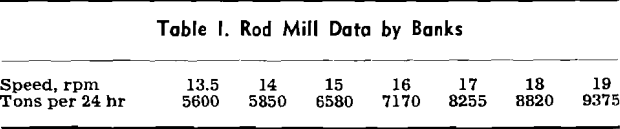
The Sullivan rod mill with its fluid drive coupling has made this test possible, a test out of the reach of practically all other grinding installations. This may be why the relationship between mill capacity and speed has not been studied earlier in more detail and why the knowledge of this relationship has been based until now on crude observations.

