Critical Surface Tension of Wetting for Minerals: Another criterion satisfying the requirement for complete wetting can be deduced from Zisman’s concept of the critical surface tension of wetting (γc). Zisman and co-workers (as reviewed by Zisman, 1963; 1964) found a linear relationship between the cosine of the contact angle and the surface tension of a homologous series of n-alkanes when contact angle measurements were conducted with low energy solids (polymers). The intercept of this linear cosΘ vs. γL, relationship at cosΘ=1 was termed the critical surface tension of wetting, which can be determined either graphically (Figure 2) or using the linear equation:
cosθ = 1 + b(γC – γL)………………………………………………………………………….(3)
where b is a constant for a given system.
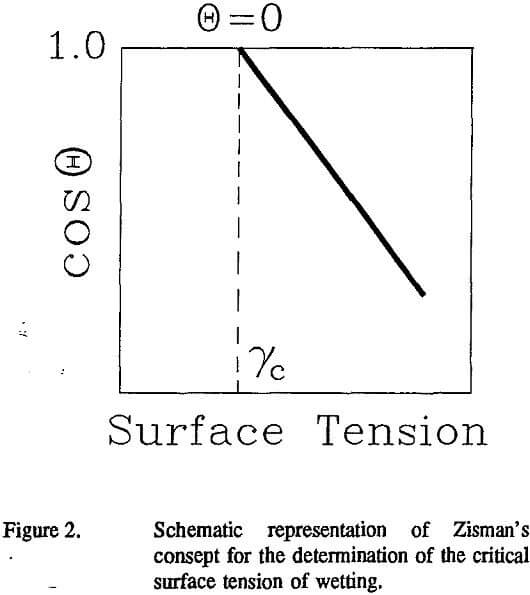
Unfortunately, the values for γc vary depending on the set of liquids used in the contact angle measurements. In particular, liquid solutions such as surfactant or alcohol solutions and hydrogen-bonding liquids are not recommended for use in the determination of the critical surface tension of wetting (for a recent review see Kloubek, 1992). The preferential adsorption of selected components at a liquid-solid interface from solution or a specific interaction between a liquid and a solid surface can affect the contact angle values significantly (Bernett and Zisman, 1959; Dann, 1970; Murphy et al., 1972). On the contrary, the concept of a critical surface tension of wetting has been found to be very useful in the analysis of mineral flotation, even when only aqueous surfactants or alcohol solutions are used (Finch and Smith, 1979).
Zisman’s criterion predicts that complete wetting of a solid surface by a liquid (it could be a mineral surface wetted by liquid polymer) can be achieved when the surface tension of liquid does not exceed the critical surface tension of wetting of the solid surface, γL<γc. Wetting characteristics as they relate to the critical surface tension of wetting for low-energy solids (surface free energy less than 100 mJ/m²) including polymers, are available in several textbooks (i.e., Wu, 1982; Kinloch, 1987). By a way of example, Table 3 presents critical surface tension data for selected polymers. Based on these data, the wetting behavior of a liquid at a polymer surface can be predicted. A liquid spreads over the polymer surface when the surface tension of the liquid is less than the critical surface tension of wetting for the polymer. When γL<γc, the liquid forms a lens with a contact angle of θ>0. Such a clear understanding of the wetting characteristics for high-energy surfaces (inorganic minerals and metals with surface free energy γs>100 mJ/m²) does not exist, and any generalization of liquid behavior at high-energy solids may fail. As discussed in a previous section, the complications of the wetting characterization of high-energy solids arise from the following problems: (a) almost every organic liquid spreads freely on smooth, clean, high-energy surfaces so the critical surface tension cannot be determined based on contact angle measurements for a homologous series, (b) “autophobic liquids” form their own adsorbed oriented monolayers at high- energy solid surfaces and these monolayers inhibit further spreading of the liquid, and (c) the wetting characteristics of many high-energy surfaces change when exposed to the environment through the adsorption of organic contaminants or water, or through chemical interaction with oxygen, water, or other gas (air) components.
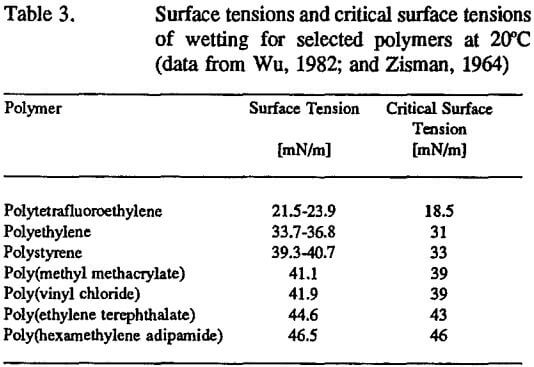
The values of the critical surface tension of wetting have been determined for a few minerals and are presented in Table 4. Alcohol-in-water solutions and liquids with high surface tension (but no homologous series!), i.e., water, diiodomethane, formamide, etc, were used in contact angle measurements. Assuming that the concept of the critical
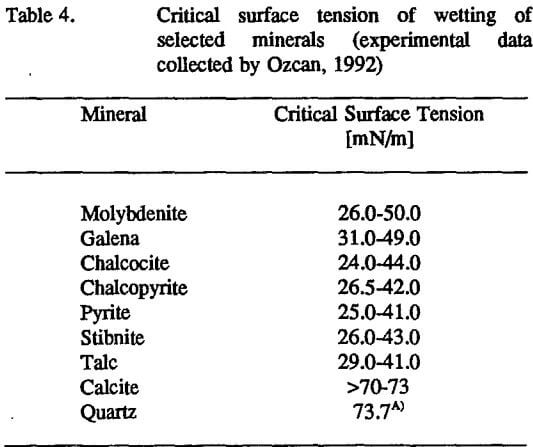
surface tension of wetting is applicable for polymer-mineral composites and that the γc values from Table 4 are representative values for the listed minerals, a simple analysis of the wetting behavior of polymers at mineral surfaces can be performed based on these data. (Unfortunately, contact angle data for molten polymers at high-energy surfaces are published rarely (Dettre and Johnson, 1970), and thus, no systematic analysis of such systems could be performed for this contribution. This area of investigation needs further research.). The surface tension values for polymers were presented in Table 3. It follows from the concept of the critical surface tension of wetting that molten polytetrafluoroethylene should spread spontaneously over the surface of any mineral listed in Table 4 (the temperature coefficients of surface tension were assumed to be the same for the polymer and mineral in order to simplify our discussion). Calcite and quartz should be covered easily by all of the polymers specified in Table 3. Polyethylene, polystyrene, poly(methyl methacrylate), and polyvinyl chloride) may or may not spread at molybdenite, galena, chalcocite, chalcopyrite, pyrite, stibnite, and talc depending on the value of the critical surface tension of wetting which is selected for this analysis from the range of data presented in Table 4. Evidently much more experimental work must be done to determine the γc values more precisely and to examine the wetting behavior of polymers at mineral surfaces. The experimental γc data vary widely (see Table 4) according to the method of measurement, mineral surface preparation, and the liquids used for the contact angle measurements (methanol-in-water solutions and pure liquids with the surface tension γL>40 mN/m). Due to the scatter in experimental data (Table 4), the values of the critical surface tension of wetting for these minerals seem to be uncertain. It is interesting to note that a similar range of γc values (γc=25- 46 mN/m), as those shown in Table 4, were reported by Zisman (1975) for several metals, glasses, alumina, and metal oxide (Fe3O4) when these surfaces were covered with adsorbed water. Zisman’s experiments clearly indicate that for some systems the measured value of γc reflects the nature of the surface contamination rather than the nature of the substrate (mineral in our case). The large difference between the γc values obtained for the same mineral (as presented in Table 4) are due to, among other factors, mineral surface contamination.
Also, molten metals have been used to examine the wetting properties of inorganic compounds but recent analysis of such experimental data indicates that Zisman’s relationship does not appear to be valid for the metal-mineral systems (Asthana, 1994). These results also suggest that Zisman’s concept of the critical surface tension of wetting, although useful for a characterization of polymer surfaces, might not necessarily be applicable for all minerals.

