Table of Contents
The energy-size reduction relationship was the dominant form of mathematical model used in the description of tumbling mill grinding processes. Typically, in these models some single measure of product fineness (e.g. the 80% passing size, the size modules, the specific surface area) is chosen as the dependent variable and the energy input per unit mass of material being ground acts as the independent variable. In some instances these models have been useful for the correlation of experimental data, but, invariably, they have been found to be inadequate for meaningful process simulation.
Experimental Data
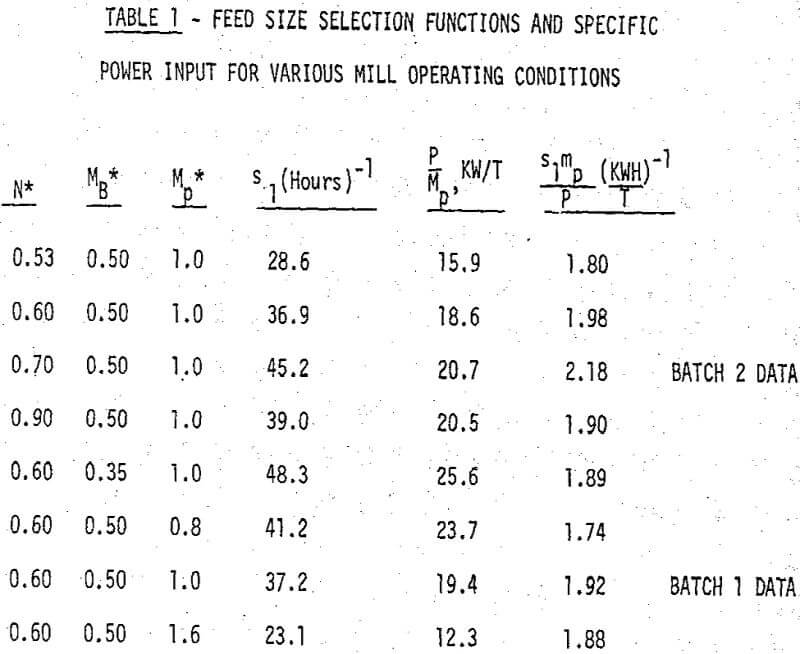
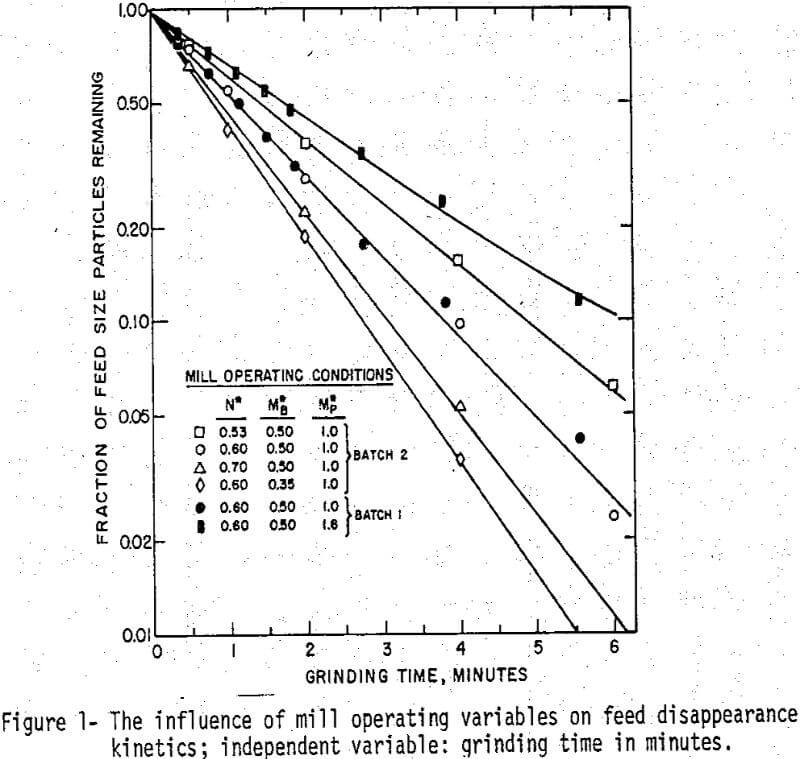
The data examined here is a composite of data collected in two separate studies designed to evaluate the influence of various mill operating variables on the kinetics of dry batch ball milling. In each of these studies the feed material was 7 x 9 mesh dolomite prepared by nipping large single crystals in a roll crusher. Since there were small differences in the fragmentation characteristics of the two batches of feed used in these studies the two data sets associated with these feeds will be distinguished by referring to them as BATCH 1 data and BATCH 2 data in the text.
The range of mill operating conditions considered in this paper is confined to that, for which the kinetics of breakage have been found to be linear to a good approximation. In terms of dimensionless mill speed, N, ball load, MB, and particle load, Mp, this range is as follows:
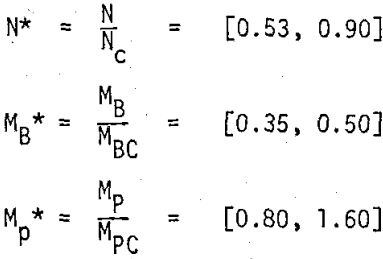
Predictive Simulation
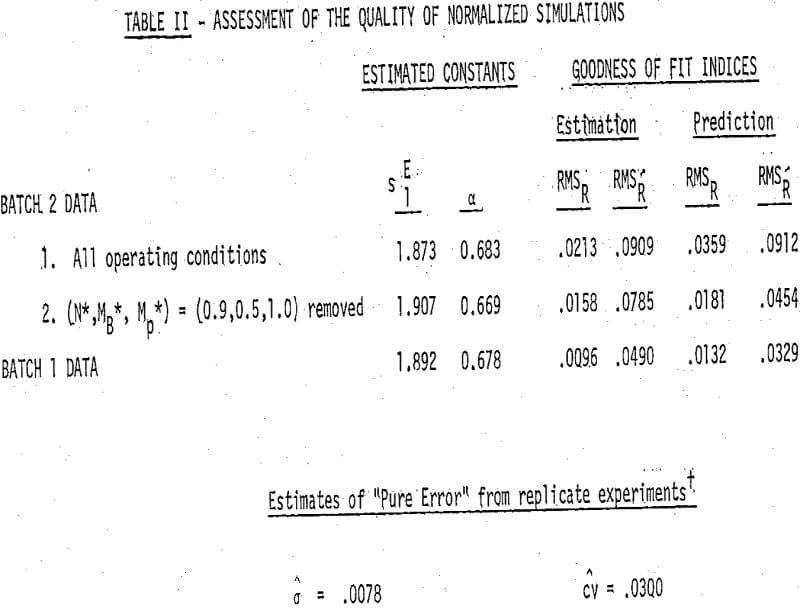
The extent to which the normalized model is useful for simulation is best evaluated by testing its predictive capability using available experimental data. This entails finding the best fit values of the model constants from a certain small portion of the available data and then using these values in the model to predict the product size distribution for experimental conditions which differ significantly from those used to estimate the model constants.
Because of the difference in breakage functions observed for the two feed materials being examined here, the BATCH 1 and BATCH 2 data sets were treated separately. In each case the average values of the breakage functions. The reduced selection functions for each feed material were estimated from size distribution data obtained for two experimental grinding times (60 and 200 revolutions for Batch 1, 1 and 4 minutes for Batch 2) from each of the mill operating conditions listed.
Having obtained estimates of the constants in the reduced model. The model predictions and experimental observations obtained for the two batches of data are shown. It has been shown that for the dry ball milling of dolomite the following approximations apply over technologically important ranges of mill operating variables:
- The size discretized selection functions are proportional to the specific power input to the mill.
- The breakage functions are invariant
These approximations gave rise to a form of the batch grinding model in which the kinetics of breakage for different mill operating conditions are normalized with respect to the specific energy input to the mill. This normalized model was shown to provide relatively accurate predictions of batch grinding behavior over a wide range of mill speeds, ball loads and particle loads. The findings presented here have been completely empirical in origin. The original correlation between the kinetics of feed disappearance and the specific energy input. Although quasi-theoretical arguments can be made to justify the normalized model, a rigorous theoretical analysis of this phenomenon is, at the present time, precluded by our lack of understanding of the complex stress application environment which exists in a tumbling mill.
If the generality of the approximations identified here is borne out by experimentation in other mill-material systems, the engineering implications could be far reaching. The ability to predict the changes in model parameters which will result from the manipulation of mill operating variables would be a definite asset in certain types of automatic control applications.