Table of Contents
A physical model of flotation, derived from viewing froth as a kinetic species since it constitutes the carrier of ore particles, not only agrees with and is simulated by engineering math models, but is statistically verified by actual laboratory flotation data. The model couples the mechanical removal of froth using paddles with the more rapid chemical interactions taking place in the bath. It clearly shows that the kinetics of mass removal is dictated by flotation cell dimensions, paddle speed, and, more importantly, froth characteristics.
The operation of industrial flotation circuits requires an evaluation of plant performance based on the recovery and grade of valuable material. The response of the circuit to changes in those factors which influence the flotation behavior the most must be identified; they are often incorporated into a mathematical model which simulates the flotation performance. In order that predictive capability is possible using a mathematical model, flotation kinetics must be assumed or derived from theoretical considerations. Many theoretical kinetic models do not lend themselves to easy analysis because of the large number of parameters which must be evaluated.
Physical Model of Flotation
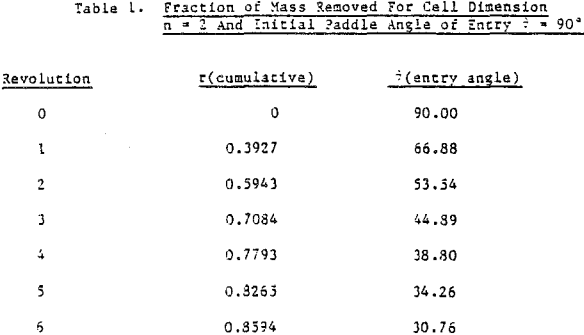
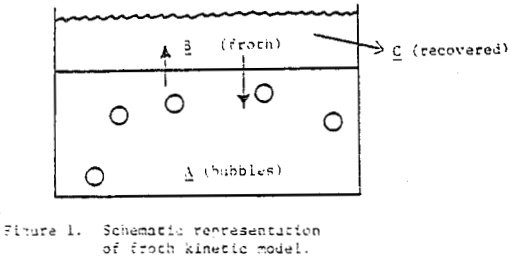
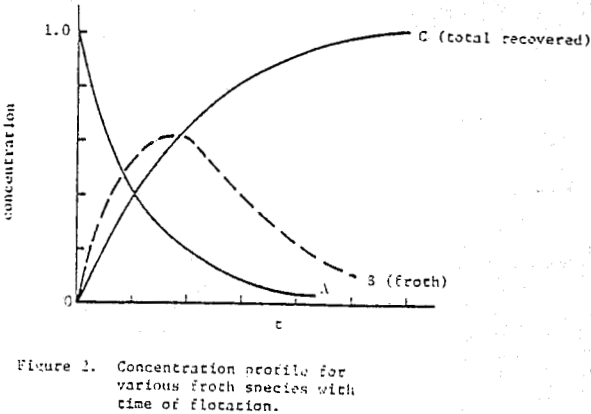
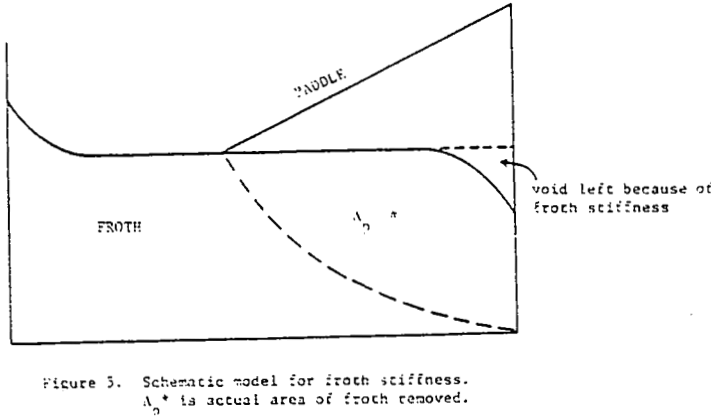
The first premise, based on visual observation, is that the froth volume or height above a float cell reaches a maximum very quickly and much faster than its removal. This is borne out in batch experiments where each increment of cumulated recovery continues to decline with time once the froth is established. The froth height and density (containing the solid particles of interest) can be considered to be in equilibrium with “potential” froth (and particulates) residing in the pulp and not yet formed or floated. This concept allows for both froth formation and destruction at the water-air interface of the cell, particle-particle exchange with the froth layer, either for a monodisperse feed or specific size distributions each with its own rate of exchange or equilibrium constant, and is not dependent on having a uniformly mixed froth phase.
An idealized case will first be considered to develop the working relationships that describe mass removal, then build in complexity to more realistically fit an actual experiment. The solids content of the froth is assumed constant over most of the experiment, at least until the latter stages of a batch run. Laboratory observations show this is approximately correct. It is again assumed that the froth height or volume is established very fast and in its entirety compared to its removal.
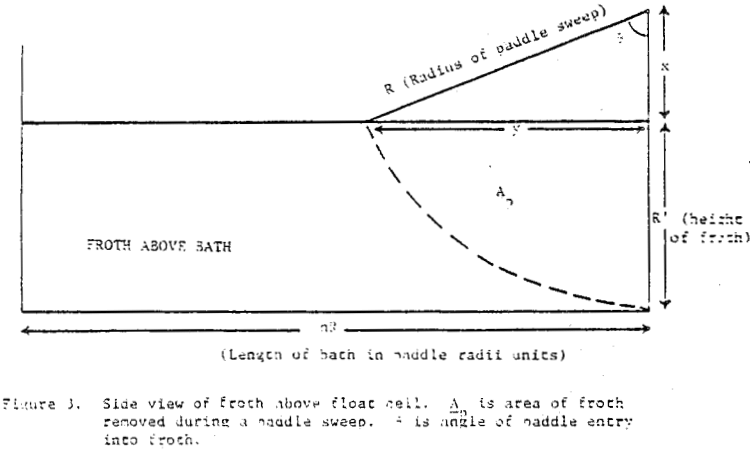
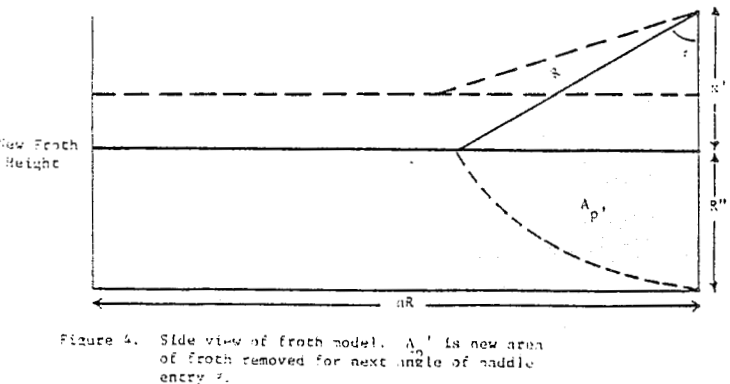
How then, should the generation of new froth be created in the mechanical model of mass removal? It is possible to view froth removal like a pair of bib overalls being processed through an old washing machine containing a wringer; the large bulky part is wrung out first with less material being squeezed at the end. Whether the overalls are folded over in the tub or stretched out straight above the tub before being wrung out is immaterial to the wringing process. In like manner, future froth which is produced in the float cell can be considered to occupy space behind the froth which is formed first.
Copper Sulfide Flotation
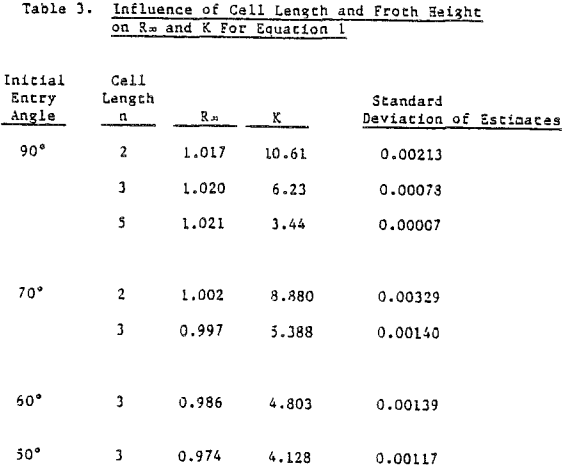
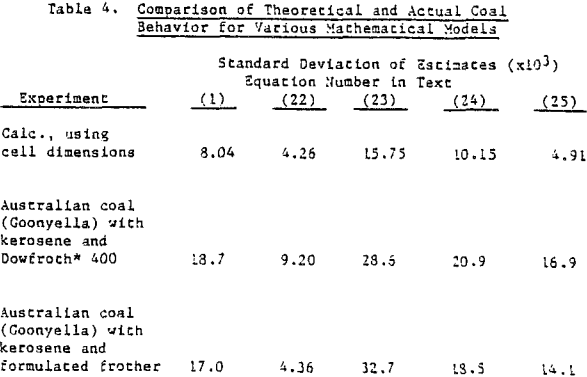
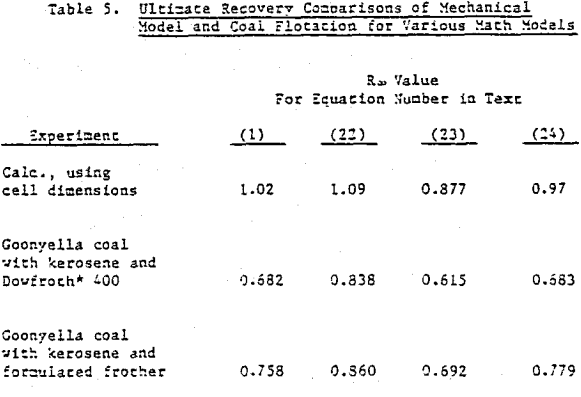
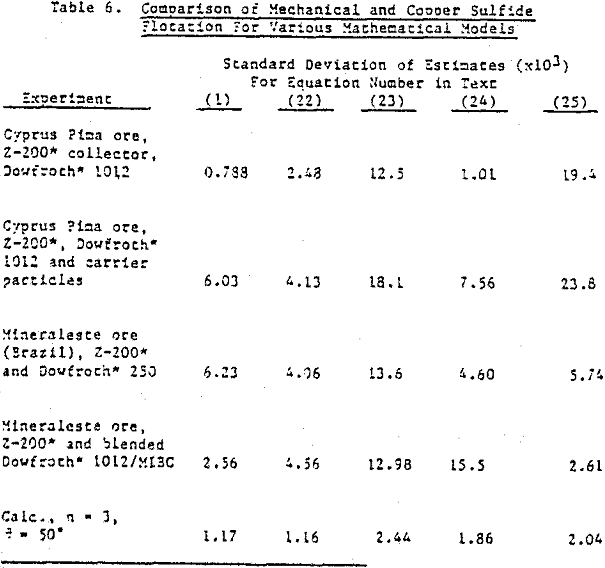
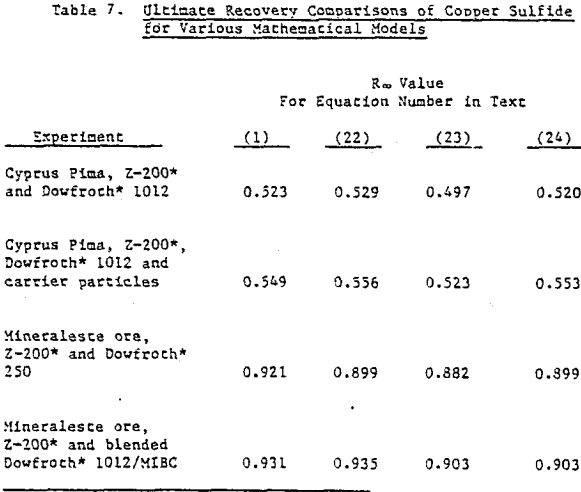
Coal is somewhat unique in that it constitutes the major component of the pulp and is the floated species. The possibility exists that the froth generated in coal flotation coincidentally agrees with the mechanical model. Copper sulfide ore, being more dense and with floatable valuable material of about 1% or less, is a much more stringent test for model simulation. When data is restricted to recoveries that do not include values less than 75% of R∞, in the time-recovery curve. It is difficult to distinguish comparative agreement among the remaining mathematical models.
Mechanistic Implications of Mechanical Model
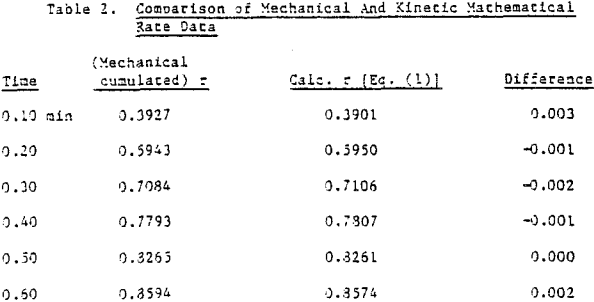
Several important implications emerge from the agreement between the mechanical model flotation behavior and actual flotation data. If Equation 1 in fact provides a sufficient kinetic simulation for both types of flotation, is it possible that this kinetic expression reflects certain significant physical interactions which take place in the float cell and are mirrored by the mechanical rate of mass removal?
For example, a collector influence on flotation rates has been noted. Enhancement of flotation rates probably resides in what transpires in the cell bath. But the mechanism by which this enhancement takes place cannot be discerned from the rate data, since it could be argued that one collector adsorbs more strongly on the ore surface than another, thus increasing the efficiency of inelastic collisions between bubbles and particles, and increasing the equilibrium in favor of the froth phase.
On the other hand, some collectors may modify bubble size distributions or their hydro-dynamic properties in the bath, and may even become part of the bubble envelope and influence particle-bubble attachment because of this change in bubble composition. Experiments of a completely different design are needed to explore the basic physical processes of flotation. Batch flotation experiments provide only a statistical correlation of the results with the effect of an experimental variable (reagent dose, type of reagent, temperature, pH, etc.) without revealing the physical basis of the correlation.