Table of Contents
While reflecting on the subject of my present paper, I soon realized that it would be very difficult to say something really new about any special aspects of metallurgy. In consideration of the excellent scientific work that has been done in the United States in connection with almost all the fundamental questions that are of interest today, and of the remarkable abstracts delivered before this Institute and elsewhere in America, I am fully aware that I run the great risk of annoying you by a detailed account on a single problem. I have therefore preferred another method. It is not my task to teach you something, as there is no doubt that you are as familiar with the problems involved in physical metallurgy as I am, or even more so, but I would rather discuss the matter with you. I trust that this discussion will be useful for both you and me, and I hope, that it will be very instructive for myself.
Before beginning the discussion, it may be well to explain the sense in which the term “physical metallurgy” will be employed in my lecture. On the one hand, metallurgy is understood to be the art of gaining metals from their ores by reducing them from their nonmetallic compounds. This domain may be called “chemical metallurgy.” On the other hand, it deals with all the methods of treating metals, once they have been obtained in the metallic state, and with all the properties of metallic systems. In other words, it covers the whole science of metals from the standpoint of their internal structure. The structure is here understood in the widest sense of the word and refers to the atomic arrangement as well as to the macrostructures of a metal. This domain of metallurgy may be called “physical metallurgy.” If I am not mistaken, this terminology has been suggested by Dr. Rosenhain.
We shall deal only with the theoretical views of physical metallurgy and not with its practical applications.
In comparing the problems of physical metallurgy of 20 years ago and those of today, we notice a typical change. Physical metallurgy 20 years ago was almost entirely understood to be the doctrine of the constitution of alloys. The investigation of constitutional diagrams was almost the sole problem dealt with in metallography. In other words, the problem was to define the crystal phases of an alloy system, their stability ranges and their composition.
The formal laws of heterogeneous equilibrium constitute the basis of the constitutional diagram. This thermodynamic basis has two peculiarities. First, it does not deal with any atomic problems. Its statements are restricted to the number and compositions of thermodynamic phases that are in equilibrium. This restriction, as given by the great American physicist J. Willard Gibbs, has been very useful, because it has enabled the scientist to study heterogeneous equilibria without using the calculations of homogeneous equilibria, which previously had been tried in vain. And, second, it neglects the influence of the surface and of the shape of phases that must be taken into account in the full statement of equilibrium conditions. We know, for example, that the vapor pressure of a liquid depends upon its radius of curvature. Only by neglecting this dependence and assuming that the surfaces are almost plane does one obtain the phase rule, which states that at a given temperature a liquid has a determined vapor pressure. The particles seen in the microscope are, from the atomistic point of view, in general so large as to enable the phase rule practically to be applied to the study of the constitutional diagrams. This law was the reliable guide, without which important progress in the physical metallurgy of 20 or 30 years ago would have been impossible.
But today the most interesting problems of physical metallurgy are of atomic character. In this respect, physical metallurgy has a share in the development of the other physical sciences. You are well aware that physics plays a leading part in the natural sciences of today. These sciences increasingly employ almost all physical methods of investigation, and the limiting line between them and pure physics can often hardly be discovered. It is the increasing application of X-ray analysis, that has mostly caused this development.
This change from formal thermodynamics to the atomic theory has taken place gradually. The plasticity of metals was perhaps the chief problem subject to such development. It was rather thoroughly investigated by Ewing and Rosenhain as early as in 1900, but in Germany it did not become an essential problem of physical metallurgy until a decade later (1912) following the research work done by Heyn and by Tammann. The plasticity of metals is connected with the important problem of the crystallographic slip, and this is naturally an atomic problem. Unfortunately, this problem is so difficult that the atomic mechanism of the slipping process is at present almost as obscure as it was 20 years ago. It is obvious, of course, that formal thermodynamics, or the phase rule, cannot help us here.
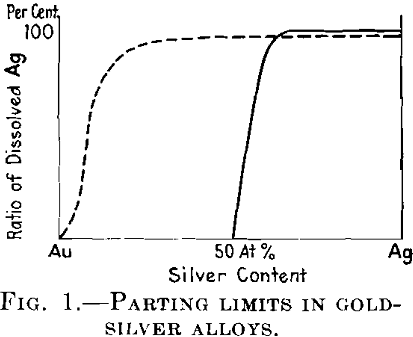
Another important problem was initiated by Tammann at the beginning of the World War. He stated that certain alloys which give an uninterrupted series of mixed crystals, as for example the silver-gold alloys, are not attacked at all by a reagent dissolving the less noble metal, provided the concentration of this metal is less than 25 or 50 atomic per cent (according to the nature of the reagent), but that the amount of this metal dissolved in such reagents rises quickly and reaches 100 per cent as soon as this concentration is exceeded. This means, for example, that from the alloys of silver with gold that contain more than 50 atomic per cent of silver almost all the silver is dissolved in the nitric acid, whereas the gold remains unattacked. Tammann called the concentration at which the less noble metal begins to be dissolved the parting limit.
The most unexpected discovery of such parting limits and of the protecting power of the noble metals in their alloys greatly affected the question of the atomic arrangement in mixed crystals. This atomic problem was first investigated by chemical means and by statistical calculations and later with the aid of X-rays. We shall study it more closely in the following discussion.
Actually, the constitution of alloys is still one of the main problems of physical metallurgy, but its meaning is now quite different from what it was before. At present, we regard it as the atomic lattice structure, as investigated, for example, by Westgren, and not merely the structure to be seen in the microscope.
Furthermore the problems of diffusion, of the building and of the development of new crystal kinds in an alloy have been investigated for more than 20 years past. These are typical atomic problems. Age-hardening is one of them, and we shall deal with it later.
This change from the thermodynamic to the atomic standpoint has given physical metallurgy many chances of advance, but has also led to some theoretical difficulties. The human mind is naturally to a certain degree one-sided. Every theory has a positive content of statements and neglects at the same time questions that are of minor interest for this particular theory. These defections are likely to be forgotten, and the theory enlarged until it reaches a point where it cannot stand its ground.
If a new theoretical view is started, which is capable of clearing up questions left more or less obscure by the preceding theory, many difficulties and apparent contradictions arise, which, on the one hand, obstruct the development of the new theory and, on the other hand, tend to abolish even valuable parts of the old theory.
I wish to discuss some of the problems of physical metallurgy from the point of view indicated above; in other words, point out the transition from the doctrine of heterogeneous equilibria to the atomic point of view and the peculiarities and difficulties arising from this transition.
Parting Limits
We begin with the theory of parting limits. The behavior of such alloys as Ag-Au against a reagent such as nitric acid, which attacks only one component of the alloy, has been pointed out above. See Fig. 1.
From the point of view of thermodynamic equilibrium, such a behavior cannot be understood. In the case of equilibrium, a certain value of electrolytic dissolving power corresponds to each concentration of the alloy, and the process of solution of silver in the electrolyte can be counterbalanced only by the osmotic pressure of silver ions in the electrolyte. If the electrolyte contains a certain amount of silver, the concentration of silver in the alloy can never fall to zero, as has been found after short
times of reaction with the nitric acid when the alloy contains more than about 62 per cent of silver, and it must gradually be reduced to zero from alloys of all concentrations, if the acid does not contain silver ions. But the fact that the reaction with the acid ceases practically completely as soon as the concentration of silver in the alloy falls below 50 atomic per cent, in other words below the parting limit, cannot be explained with the aid of thermodynamics. Its explanation is only possible if we assume that inner diffusion of the alloy, as a state of a movable equilibrium, does not exist at the temperature concerned and that the arrangement of the atoms in the crystal lattice is such that the atoms of gold protect the atoms of silver from the reaction with the acid.
For reagents that are weaker and mostly bivalent, the parting limit lies at 25 atomic per cent. (Later we shall see that this assertion is only approximately correct.)
How can an atomic arrangement explain the existence of parting limits at 25 and at 50 atomic per cent? Before answering this question, one must have a conception of the path enabling the reagent to penetrate into the inner part of the metal.
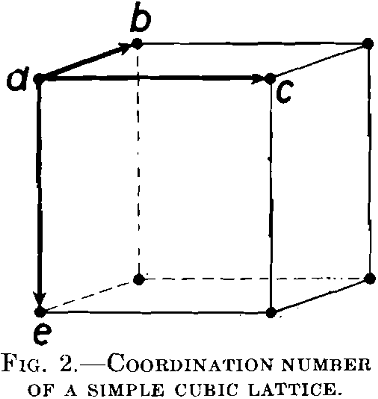
Let us consider a simple cubic lattice, Fig. 2. The shortest distances between atoms are along the borders of the elementary cell. For every atom a, there are six atoms surrounding it at the shortest distance d; namely, the atoms b, c and e in the primitive cell represented in the figure and three others in the neighboring cells. G. Tammann has supposed that the reagent can proceed only from one nonresistant atom to another, the shortest distance away, and that an atom a is protected from the action of the reagent if no atoms in the immediate neighborhood are attacked by the reagent, because they are noble or because they are protected in one way or another.
The solution of the reactive atoms is therefore considered to proceed from the surface along “coherent paths” of reactive atoms, in which two neighboring atoms are spaced at the shortest possible distance in the space lattice concerned.
Tammann has tried to calculate the resistance of an alloy by means of a statistical method, under the assumption that the atoms of both metals in the lattice are distributed at random. Let the atomic concentration of the reactive atoms be p, and of the noble atoms q. (p + q = 1) Consider the reactive atom a, Fig. 2. Evidently it will be protected, if it is surrounded by six nonreactive atoms. For this purpose, there must be a group of seven atoms in the arrangement indicated in Fig. 2. The probability of such a group is in accordance with the theory of probabilities: 7qp6, if it is assumed that the reactive atom p may have any given position; viz., in the middle of the group, as well as at one of the other points. From these seven positions it would be protected only in the first. The probability of such a protective group is therefore only one-seventh of that mentioned above, therefore simply: p · q6.
There are still other protecting groups containing two or more reactive atoms. To be protected, these atoms must be surrounded by more than six nonreactive atoms. Therefore it becomes necessary to consider groups containing much more than seven atoms. The more atoms a group contains, the less is its probability value.
All the larger groups together give much smaller probability values than does the group having seven atoms. By adding all these probability expressions, Tammann obtained the probability of protection of the reactive atoms in dependence on the atomic ratio. If the numbers of the atoms considered are, as practically in every crystal, very large, this probability number gives the ratio of protected reactive atoms in the whole crystal. In this way he obtained the dotted curve in Fig. 1 as against the straight line found experimentally.
This contradiction between the calculated and the experimental results has led Tammann to the conclusion that the basis of the calculation was erroneous; in other words, that the atoms in a mixed crystal must be arranged in a regular manner (symmetrically).
Tammann has calculated the possible regular arrangements in different crystal lattices at different concentrations and has pointed out that the parting limit is likely to lie preferably at 25 or 50 atomic per cent of the components. It is not necessary for us to elaborate these ideas, because it has been proved since by means of X-ray investigation that the atoms are distributed at random in the alloys of copper and gold, if fairly quickly cooled. Let us consider a face-centered cubic lattice and let us assume that the regular arrangement of atoms is such that the atoms of gold lie in the corners, whereas all atoms entering the faces of the unit cube are of copper (Fig. 3). This corresponds to 25 atomic per cent of gold. In this case, we should expect on the X-ray Debye film the so-called “superstructure” lines corresponding to the identity period d, this
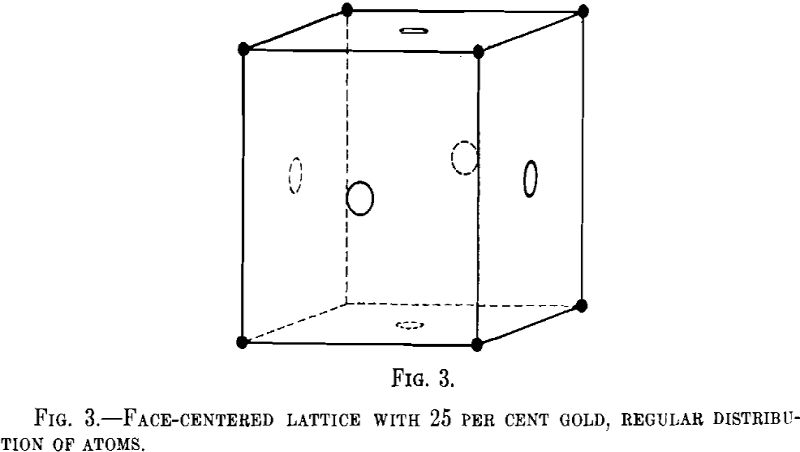
signifying the shortest distance from point to point at which the atomic arrangement is repeated, as against one-half the identity period in the random arrangement of the atoms.
No superstructure lines have been found in the alloys of silver with gold. In the alloys of copper with gold, the superstructure lines appear only after tempering below the transition points at 400°, but the parting limit is developed with alloys not treated in this way. Thus it is clearly proved that no connection exists between the parting limits and the regular arrangement of atoms in the lattice.
But how can the existence of parting limits and their position at definite concentration points then be explained, since the statistical calculation of Tammann has led to quite a false result?
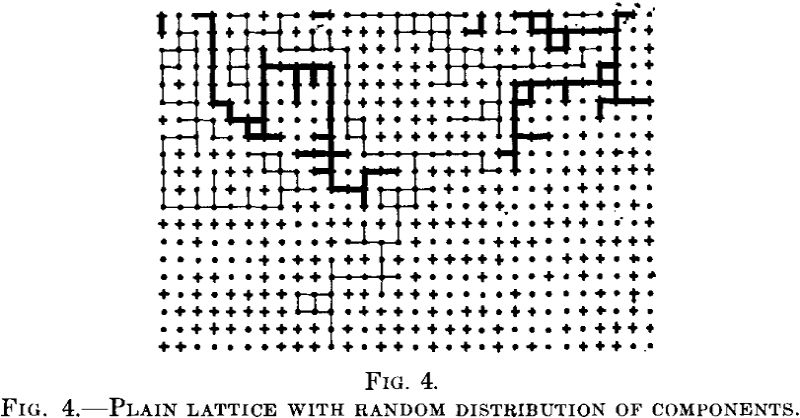
This calculation is incomplete. Consider the two dimensional lattice models in Fig. 4.
Let the points be the noble atoms and the crosses the reactive ones. Their arrangement is an irregular one. Let us now consider the coherent paths of reactive atoms from the upper end of the lattice. If the reaction proceeds along these paths, only such atoms as lie there will be attacked by the reagent; all the other reactive atoms will be protected. Now there are large areas into which the reagent does not penetrate at all, regardless of the position of single atoms in these parts as Tammann conceived it.
Apart from the protected positions of reactive atoms envisaged by Tammann, there are conditions that enable entire blocks of crystals to be protected. These conditions were neglected by Tammann.
How can the probability of such protective conditions be calculated? I have tried to do this in the following way:
The principles underlying such a calculation may be seen from a plane model lattice, Fig. 5, which is the lattice shown in Fig. 4, but turned through an angle of 45°. Let us suppose that the attack is proceeding
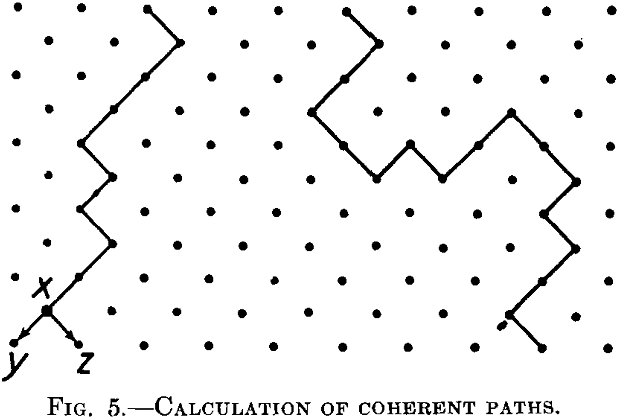
from the upper end along coherent paths, and let us introduce one restriction. The attack can proceed from the upper to the lower part, but cannot be reversed. In other words, paths such as the one indicated in Fig. 5 on the left are possible, but paths similar to the one on the right are not possible. This is, of course, quite an artificial restriction, but it simplifies the discussion to a large extent and has for this reason been introduced by Borelius.
We consider a great number of the paths as in Fig. 5 during the step-by-step progression of the attack of the reagent into the inner part of the lattice. We try to calculate the chance of the reactive atoms being reached by the reagent progressing in this way. If the reagent has reached the point x, it can proceed further in two directions, to y and to z. If both are reactive atoms, the number of the atoms attacked by the reagent at the steps corresponding to y and z will be greater than at the step x. If both atoms are resistive, the path will be abruptly terminated at x. We consider the mean ratio of the number of reactive atoms reached by the reagent at the step y, z to the same number at the step x, for a great number of paths such as the left in Fig. 5. If this ratio is less than unity, the coherent paths will die away one after the other, the reagent will be capable only of penetrating into the superficial layer of the lattice and the body will be resistant. If this ratio is greater than unity, the paths will be gradually increased by the developing of new branches and the reagent will penetrate into the whole alloy.
The parting limit lies obviously at the concentration point where this ratio is equal to 1.
The probability that at the point y or at the point z there will be a reactive atom is simply p, if p is the atomic concentration of this atom in the lattice under consideration. The required ratio R will then be R = 2p, or the parting limit = 0.5 = 50 per cent, in agreement with experiment. Nevertheless this result is erroneous. We have deduced it by assuming that, at least in the neighborhood of the parting limit, the different paths will be sufficiently remote one from the other to avoid mutual interference. In other words, we suppose that the reactive elements actually reached by the reagent are distributed statistically over every step of the path under consideration. But this is not so. The distribution at the step y, z is, for example, not independent of the distribution at the foregoing step.
Therefore it cannot be calculated statistically, and it is possible—and proves to be so—that different coherent paths interfere with one another even in the neighborhood of the parting limit.
Borelius has calculated the parting limit in a somewhat different way. But since he also assumes a regular distribution of the attacked atoms in the inner part of the lattice, he obtains the same false result that I do.
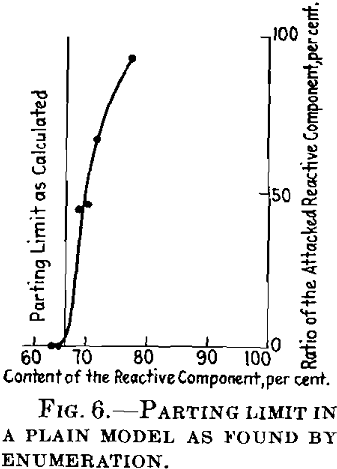
By a simple construction of coherent paths on a model lattice, Fig. 5, and by counting the attacked atoms, we obtain a parting limit a little above 66 atomic per cent of the resistant component, as I have shown above. Fig. 6 shows the ratio of the attacked atoms at different concentration points.
I have tried to avoid this fault by a modified calculation. This becomes very troublesome but I have succeeded in calculating the parting limit approximately between the atomic ratios 0.651 and 0.67 of the noble component, which is in close agreement with the result of the experiment by graphic enumeration. It has therefore been proved with the help of the model that there are marked parting limits, even when the atoms are distributed at random. This result is very likely to hold for three-dimensional lattices. There now remains the discussion of the concentration at the parting limit.
I have already mentioned that it seems to be almost impossible exactly to calculate this limit in a real crystal.
But there appears to be another possibility of dealing with the problem, as has been shown by Borelius. In a plane lattice like that of Fig. 4, the condition of corrosion resistance of the alloy is that the coherent paths of the reactive atoms terminate in the neighborhood of the surface. But this means that they must be surrounded by coherent chains of resistant atoms. The condition of resistivity is then the existence of coherent paths of resistant atoms and the condition of reactivity of the alloy, the existence of similar paths of active atoms. Therefore the parting limit can lie only at the atomic ratio 1:1; thus at 50 atomic per cent Borelius has been able to find this parting limit by counting the reactive atoms reached by the reagent on a plane model as that of Fig. 4; all the directions of closely spaced steps being admissible. Collaterally, this result proves directly that Tammann’s statistical calculation, as indicated above, is not correct. He has, indeed, computed his curve, given in Fig. 1, for four protecting atoms, as shown in the plane lattice Fig. 4. Thus the curve is in strict contradiction with the result obtained by Borelius from his enumeration method.
If we desire to apply these considerations of symmetry to three-dimensional crystals, we must operate with inner surfaces instead of chains of atoms. Hence we shall say that the action of the reagent depends on the existence of coherent inner surfaces consisting only of the one or the other kind of atoms. If the crystal is reactive, it is divided by coherent surfaces of reactive atoms into a great number of parts. It is, on the contrary, resistant if these coherent surfaces consist of resistant atoms. The two conditions exclude one another, and the parting limit must be again at 50 atomic per cent.
At first sight it seems to be very improbable that coherent surfaces should be decisive for reactivity or chemical resistance. A closer consideration shows, however, that the fundamental condition of coherent chains is less probable. The reagent (for example, nitric acid) has a molecular volume that is larger than that of the single atoms in the space lattice. This reagent therefore will not be able to proceed along such small paths as define the chains of reactive atoms. Furthermore, the products of the reaction, the metal cations and the lower nitric oxides, must be removed before the reaction can proceed further, and must be driven into aqueous solution. A far larger space is thus required for the continuous reaction than for that given in a chain of reactive atoms, and the assumption of such chains must be regarded merely as a fictitious image of the facts.
It may be assumed—and we shall enter later more fully into this question—that the reaction proceeding from the outer surface of the metallic body destroys it in some way, until it finds a barrier in a surface consisting only of noble atoms.
In this way it seems not impossible to understand that the parting limit must lie at 50 atomic per cent. But the explanation is still highly hypothetical and can be considered satisfactory only if it enables other facts to be predicted without using some new and difficult hypothesis.
We may now consider the second parting limit, which, according to Tammann, lies at 75 atomic per cent of the reactive component. Tammann has observed that this parting limit is found, if the reagent is bivalent, in the case of the ordinary 50 atomic per cent limit. Even this assertion may be considered to be indistinct; it is an established fact that the 50 per cent parting limit occurs in highly reactive electrolytes, while the 25 per cent parting limit is found in less reactive electrolytes. In the case of the 50 per cent limit the condition of the limit can be supposed to be symmetrical, so far as the single points of the lattice are concerned. They must be occupied as often by the atoms of the one as by those of the other component. The probabilities for these two events are simply given by the atomic ratios p and q for the reactive atoms P and the resistive atoms Q, respectively, and the required condition is p = q, or p = q = 0.5, since p + q = 1.
We may suppose that in the case of a bivalent or a less energetic reagent the groups containing one single atom are no longer decisive, but rather the groups set up of two atoms. This supposition is not quite new; Tammann has already employed it, in discussing parting limits on the basis of regular atomic arrangements. We shall suppose, furthermore, as Tammann did, that in such a case a group of two atoms is reactive only when it consists of two reactive atoms. If it consists of one reactive and one resistant atom, it is resistant as a whole.
The condition of the parting limit will again be that the probability of the resistant two-atomic groups is equal to the probability of the reactive groups.
The probability of the groups consisting of two reactive atoms is p², of the two resistant atoms q², and of a resistant and a reactive atom 2pq. (The sum of these probabilities must be 1.) The parting limit is therefore given by the equation
p² = 2pq + q² = 1 – p²
or
p = 1/√2 = 0.71 and q = 0.29
instead of 0.75 for the reactive component, or 0.25 for the resistant component, as given by Tammann.
Table 1 shows some values of parting limits given by Tammann for the alloy of gold with silver and of gold with copper, which have been investigated most thoroughly.
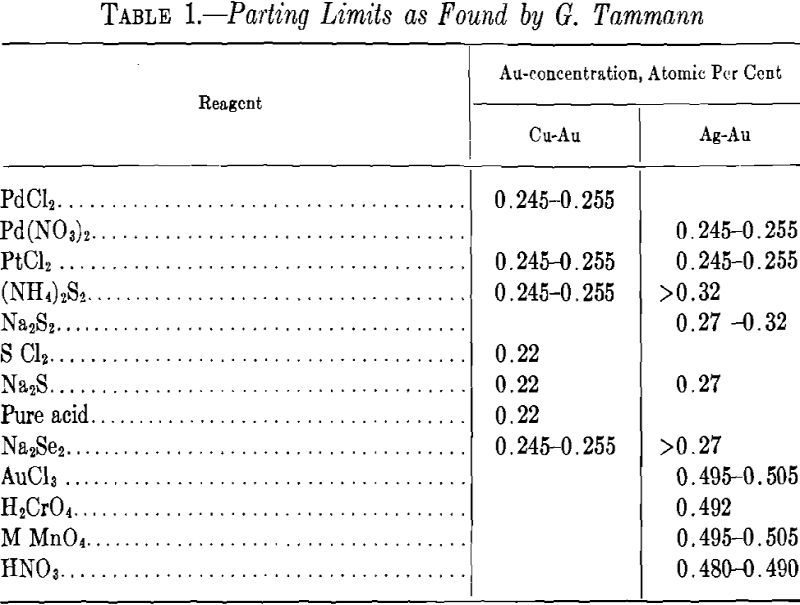
The 0.25 limit is fairly well indicated in the case of some reagents with copper-gold alloys and, to some extent, with silver-gold alloys; but generally this parting limit tends to lie in the former, below and, in the latter, above this figure for the concentration of the noble component. In general, this limit is less defined and fluctuates more than the 50 atomic per cent limit. In the silver-gold alloys, the former limit is poorly defined.
Table 1 shows that the parting limit of the silver-gold alloys lies often in the neighborhood of 0.29, as required by the calculation. The mean value as given in Table 1 of the limit for these alloys is about 0.276. The mean value for the alloys of copper and gold, about 0.233, is lower by 0.04 than for the silver-gold alloys. This deduction of 0.25 parting has been given by Dehlinger and Glocker.
Now, from the theoretical point of view, one is justified in expecting that the silver-gold alloys are more ideal solid solutions than are the gold-copper alloys, since the latter form the compounds Cu3Au and CuAu. Therefore it may be supposed that at higher temperature (above the temperature of the formation of these compounds) the affinity between copper and gold acts according to the law of the distribution of atoms in the space lattice. Let us suppose that owing to this affinity groups of two atoms of gold cannot exist in these alloys. Let us, moreover, consider a portion of the space lattice having N (a large number) of atoms, and let p and q be the ratios of the copper and gold atoms respectively with each atom surrounded by n atoms at the shortest distance (coordination number). Then the number of all groups of two atoms will be
n · N/2
The number of gold atoms is Nq and the number of groups in which the gold participates,
Nqn
All the other groups consist of copper atoms only; their number is:
n · N/2 – Nqn
These are reactive.
The parting limit is given by the relation
Nqn = nN/2 – Nqn
or
q = ¼ – 0.25
In this case, the parting limit is lowered by about 0.04 as compared with that of the silver-gold alloys.
We shall not discuss the question of the copper-gold alloys here in detail, because we stand at the moment upon highly uncertain ground. It may be mentioned, however, that if the difference between the gold-silver and the gold-copper alloys with respect to parting limits depends on deviations of the latter alloys from a simple random distribution of the single atoms in the space lattice, it should be expected that the law of the distribution of single atoms must be different at different temperatures above the temperature of formation of the compound AuCu3, which is stable only beyond about 400° C. By quenching these alloys from different temperatures and by determining their parting limits, it must therefore be possible to ascertain these changes in the law of distribution of the atoms.
Generally speaking, it is today of little value to set up any imaginary mechanism of reaction for explaining the actually observed position of the parting limits. Real advance can be made only on the basis of experimental investigation of the mechanism itself. The sole successful attempt in this direction has been made by Graf, who has investigated the reactions of different gold-copper alloys with the help of X-ray observations. He has found that the nitric acid in which the parting limit lies at 50 atomic per cent, when reacting with alloys poorer in gold than this figure, converts the space lattice into one of pure gold. The diffraction lines of gold are well defined and the orientation of the gold crystals is the same as that of the unattacked alloy. If the alloy is attacked by a concentrated nitric acid, the diffraction lines are broadened equally on both sides of the true copper value. They show in part new orientations of crystals, as, in addition to the black spots corresponding to the prior orientation, fainter continuous ranges of Debye lines may be seen.
The same effect is observed, if the alloy is treated with a mixture of nitric and hydrochloric acid, this mixture dissolving, as is known, not only copper but also gold.
By carefully etching off the surface layer of gold, Graf has been able to show that there is no gradual change of lattice constant between the unattacked alloy and the gold—evidently the latter is located upon the unaltered alloy and intermediate concentrations do not occur between the two bodies.
From these observations, Graf concludes that nitric acid is capable of bringing gold into the ionic state, but only at the weak points of the space lattice; for example, at the corners left after the solution of copper atoms. Perhaps the gold atoms are also in the ionic state on the entire surface of the alloy, with this one atomic layer held adsorbed by the underlying space lattice. Only the atoms at the “weak” points can travel in the electrolyte. But surely the degree of mobility will be higher for an ionized surface than for the atoms in the space lattice.
It may be assumed that the gold ions cannot be stable in the presence of metallic copper atoms. The copper atoms must be ionized while the gold ions are being reduced by the copper. From a general point of view, this is an electrolytic reduction of gold.
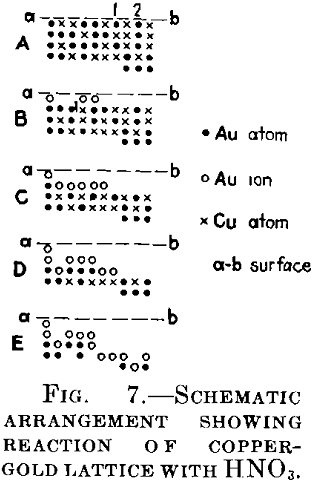
Consider the plane lattice Fig. 7A, the crosses being the copper atoms and the points the gold atoms. The upper part of the figure is assumed to be the surface at which the reaction starts. In the next moment, the atoms of copper will be dissolved in the acid and also the gold atoms 1 and 2 occupying weak positions, while the other gold atoms will be ionized. Representing the gold ions by circles, we thus obtain Fig. 7B. The copper atom will be oxidized by one of the two gold cations located above it, the other will be dissolved, as being now in a “weak” position. The gold atoms of the surface will again be ionized, the copper atoms will be dissolved and, as the next step of the reaction, we shall obtain Fig. 1C. By adding identical steps we shall obtain Figs. D and E.
In this way we have obtained an impression of the reaction process which differs widely from that of the “coherent paths” discussed above. The position of the parting limit to which this reaction mechanism may lead has not yet been calculated; but it is not impossible that it may lead to the condition of Borelius, which means that the reaction will be finished as soon as a coherent surface of resistive atoms is reached. U. Dehlinger and R. Glocker (Op. cit.) calculate the parting limit on the basis of the results of Graf in a somewhat different way. They assume that the gold atoms of the surface are movable in the sense of M. Volmer and W. Weber but are not ionized. Their mobility enables them to fill up voids left by dissolution of copper atoms; thus leading to the formation of a coherent protective layer of gold atoms. This conception uses also the results of Graf and signifies therefore a progress as compared with the former calculations. It is impossible to decide today whether the conception of Graf or that of Dehlinger and Glocker corresponds more closely to the truth. But Graf’s observations of the diffraction lines of the space lattice of gold after the action of the nitric acid are sharp in the same way as in the case of the action of nitric and hydrochloric acid together, which makes the view of Graf more probable.
As to the reaction with reagents that shows the parting limit at 25 per cent of the nobler component, Graf has found that by treating alloys containing 10 to 15 atomic per cent gold no space lattice of pure gold is formed. But the diffraction areas of the outer surface were broadened after the reaction had ceased, and from this broadening it has been calculated that the gold content of the surface layer may vary from 20 to 40 atomic per cent. Graf’s conception is that the less reactive electrolytes having a parting limit at 25 atomic per cent do not involve a transition of the gold atoms into the ionized state, but that the single gold atoms lying at the “weak” points of the surface after solution of the copper atoms are, to a certain degree, still movable, although less so than when in the state of cations. They may travel on the surface, therefore, until they fall to deeper levels and are fixed there. In this way, we may obtain broken off crystal pieces with coherent gold surface layers and various copper contents.
The question as to the mechanism of reaction producing in this case a parting limit in the neighborhood of 25 per cent is not yet settled. But it is noteworthy that although the reaction residue is pure gold with strong reagents such as nitric acid, as previously known, this is not so with the milder reagent having the lower parting limit. This is an entirely new condition, which had not been expected from the point of view of Tammann’s theory. The assumption of a solution along “coherent paths” of atoms cannot explain it.
In order to make a more definite statement as to these conditions, it will be necessary to investigate the matter more thoroughly in an experimental manner.
Aging
Age-hardening is one of the most important problems faced in present-day metallurgy both from the practical and the theoretical standpoint. Dr. Merica dealt with this problem in his lecture last year, and I am glad to say that I find myself in agreement with him at almost every point. Therefore I shall not discuss the technical questions of age-hardening but rather confine myself to a consideration of three or four theoretical questions, that seem to me most interesting today.
You are well aware that an alloy can only be age-hardened if it is obtainable at ordinary temperature in the state of a supersaturated solution. This holds for the alloy of Fig. 8, which is homogeneous at temperatures above t2 and is obtainable at room temperature t0 in the homogeneous state when quenched from the former temperature. If we raise its temperature after quenching to an intermediate value t1 the alloy will be age-hardened; that is, its hardness and strength will be increased and several other properties altered. For some alloys, for example, duralumin, the temperature t1 coincides with t0, and they can therefore be aged at ordinary temperature.
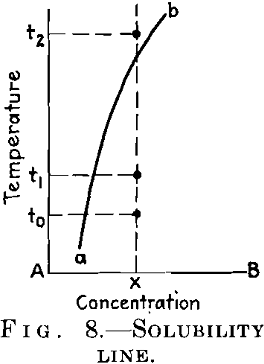
These conditions of the aging process clearly indicate that it is in some way connected with the decomposition of the solid solution. Now, the alloyed metal exists in the mixed crystal in atomic dispersion, and it is coagulated as completed crystals after the excess has been separated from the supersaturated mixed crystal and after the equilibrium has been reached. It is therefore quite evident that the intermediate state of the age-hardened alloy corresponds to some intermediate state of dispersion, or to some degree of “critical dispersion.” In this general sense, the “critical dispersion” theory of age-hardening is quite secured today. This is the first basic point I have desired to emphasize.
The second point refers to the question as to the degree of dispersion that is critical. This question has not yet been definitely solved. Surely it has a different aspect for different alloys.
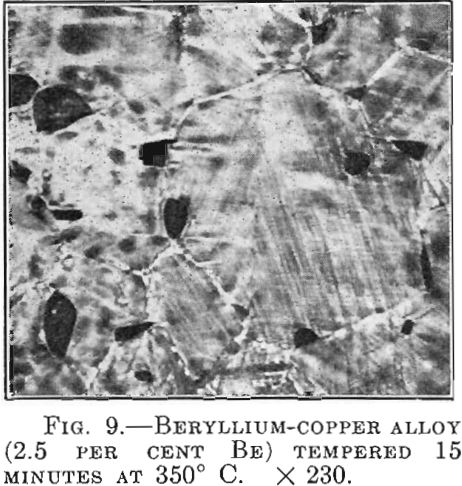
There are alloys in which the hardening is accompanied by striation on the polished surface within individual crystals. The beryllium-copper alloys behave in this manner (Fig. 9). In line with the results of the investigation with the aid of X-rays, which shows broadening of the diffraction lines of the a crystals from the beginning of the age-hardening, it is apparently justifiable to speak in this case of the segregation of a second crystal type and to assume that critical dispersion is understood to mean simply a certain magnitude of the separated γ crystals.
But duralumin and the alloys of aluminum with copper show quite a different behavior. The X-ray intensity analysis shows that the continuous background of the X-ray patterns becomes less darkened during aging as compared with the pattern of the quenched alloy. At the same time the intensity of the Debye diffraction lines rises, especially of those corresponding to the higher indices. These statements are explained by the assumption that the lattice-distorting influence of the diluted copper is lowered by aging. On this basis of X-ray interpretation it is actually taken for granted that in these alloys the age-hardening at ordinary temperatures occurs through accumulation of copper atoms into small groups within the aluminum mixed crystal, this being the first stage of a further separation. In this case the “critical dispersion” corresponds to quite another, obviously much smaller, magnitude of the nuclei and has quite another meaning.
Are the groups of copper atoms at this stage to be considered real nuclei of a second crystal type? This seems to be impossible. The lattice constant of the mixed crystal is in fact not altered by the agglomeration of copper atoms into such groups; but even if true copper nucleii groups were very small, such an alteration should be expected, since their separation would mean a change in concentration of the aluminum mixed crystal. To explain the fact that there is no noticeable change of the crystal lattice, it must be assumed that the lattice constant, as measured by means of X-rays, corresponds to a mean value between parts of maxima and minima copper content. Therefore these parts must still be optically coherent. This seems possible only if both remain in the same space lattice.
Here we have to deal with a typical problem involved in present-day metallurgy. As the classical differentiation between different phases fails to explain the phenomena, the possible intermediate states should be borne in mind. Yet it is possible that the question whether a group of copper atoms in the space lattice of an aluminum mixed crystal is a nucleus of a second phase (Al2Cu) or not is of no account. The formation of the crystals of the compound Al2Cu from the groups of copper atoms is likely to proceed continuously. These groups will form distortions in the space lattice of the mixed crystal, which will gradually increase with their increasing size, while its inner structure approaches more and more that of the space lattice of CuAl2. From the atomic point of view, the formation of a second phase can be regarded as a continuous process. The formation of CuAl2 has been recently considered in this light by Mehl.
The definitions of the classical phase rule become useless in such cases. As to such processes, it is of little use to ask how many phases there are or whether a process is a heterogeneous or homogeneous one. The designations, “phase,” “nucleus,” etc., fail in their ordinary sense, but this does not mean that they become superfluous or erroneous; they are merely not sufficient to solve the atomic problems under consideration.
But in a wider sense we may still speak of nuclei in the case of copper groups present in duralumin at ordinary temperature. The thermodynamic meaning of the formation of a nucleus is the sudden acquisition of stability. In every solution phase there occur occasionally groups of two or more dissolved atoms in close association. But if the solution is not saturated, such groups will not be stable and will disperse after a very short time into the surrounding solid solution. In a supersaturated solution there will be a certain critical inferior limit of magnitude, above which they become stable. These groups differ from their surroundings and therefore will have a term of free energy corresponding to the free energy of the surfaces in the liquid state. It is this term of free energy that makes these groups unstable if they are very small, and that loses its influence as they increase in size. When these groups reach the “critical range,” they will not be dissolved again but will remain in the original state of formation. We must therefore regard them as true “nuclei” in the thermodynamic sense of this word.
For this reason the groups of copper atoms in duralumin, or “knots,” as Dr. Merica calls them, are “nuclei,” because they are stable. Another question is whether another jump of stability is produced when these groups lose their “optical contact” with the matrix phase and become true crystals of the second phase. We have already considered this question and there is in principle no necessity for this second change.
However, there is another feature that makes it appear probable that there is a material difference between the formation of the “groups” or “knots” of copper atoms in the space lattice of the mixed crystal and the formation and growth of crystals of a second phase. Dr. Merica has directed attention to the fact that the hardness of duralumin, when once reached, has a remarkably high degree of thermal stability. Its loss seems to begin only at temperatures as high as about 200° C. In this connection, duralumin differs appreciably from some other age-hardenable alloys, such as the alloys of beryllium. For these, the hardness begins, in general, to decrease at the same temperature at which its maximum value is reached if the time of aging is unduly prolonged, while duralumin can be held for years at ordinary temperatures before the hardness starts to sink.
This great stability of age-hardened duralumin makes it probable that the “knots” of copper atoms are in some way stabilized so that the diffusion that leads to their formation ceases as soon as they are formed. An explanation for this assumption has recently been given by Dehlinger, who supposes that the knots are formed by only one diffusion step; viz., by one change of place of atoms. As the knot is more stable than the supersaturated mixed crystal, such a diffusion step must be connected with a certain affinity force facilitating the formation of the knot and making its re-solution difficult. This is therefore not a real diffusion, but rather an irreversible reaction in the solid state.
By means of a brief calculation, we can show that the formation of knots in such a process is probable even in solid solutions as dilute as duralumin with 5 per cent copper by weight = 2.2 atomic per cent copper. In this alloy about 50 aluminum atoms correspond to one copper atom.
In the face-centered space lattice of aluminum every atom is surrounded by 12 atoms at the shortest distance and by about 48 atoms at double this distance.
It may therefore be roughly assumed that a knot of 3 copper atoms can be formed if a group of about 64 copper atoms contains at least 3 atoms of copper. The probability of such a group of 64 atoms is about 0.15, as follows:

It may be supposed that the distance separating the copper atoms in the “knots” is about double that separating the single atoms in the aluminum space lattice.
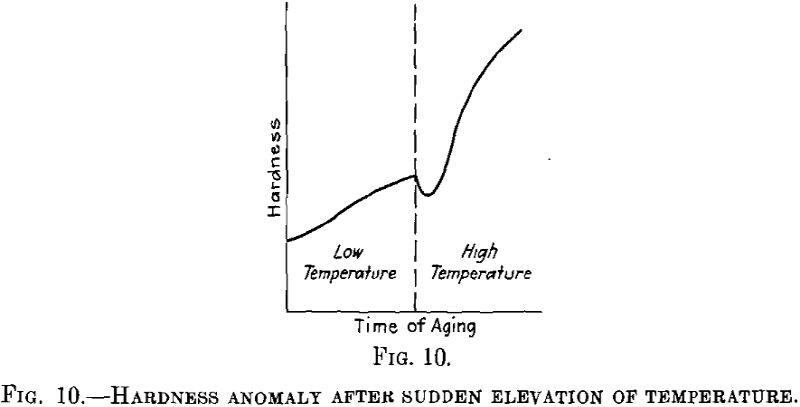
With relation to the subject of nuclei we shall deal with a third, point discussed also in Dr. Merica’s lecture; that is the fact that an age-hardenable alloy, if aged at a lower temperature and rapidly heated to a higher temperature, first loses to some extent its hardening effect before the hardening again starts at the higher temperature, as may be seen from Fig. 10. This phenomenon seems to occur in very different age-hardenable alloys.
We have studied this phenomenon in detail in duralumin, in connection with variations due to changes in the electrical conductivity, and have arrived at the following conclusions:
If during the first aging at low temperatures the conductivity decreases, it rises at once
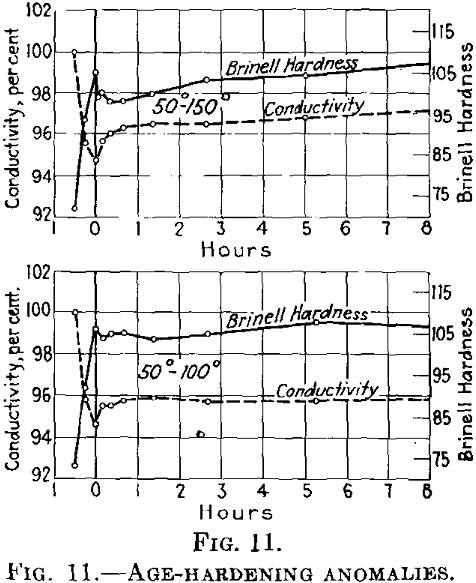
in an accelerated manner after being heated to higher temperatures.
In this case, the reduction in hardness involves increased conductivity (Fig. 11). If the conditions at the lower temperature are such that the conductivity after decreasing rises again (in other words, if the initial temperature is higher than as shown in Fig. 11, the conductivity first drops after rapid heating to the second (higher) temper-
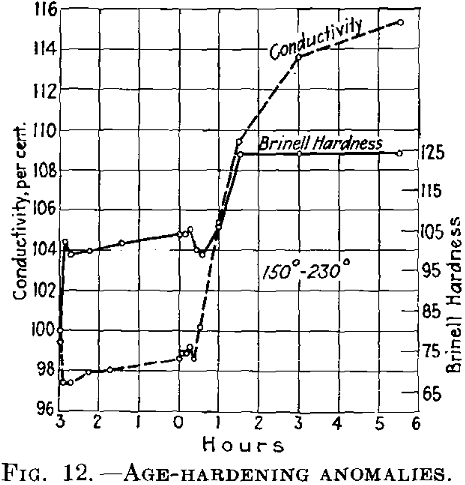
ature and then rises again (Fig. 12). The last rise corresponds to the normal behavior of duralumin when treated at this temperature.
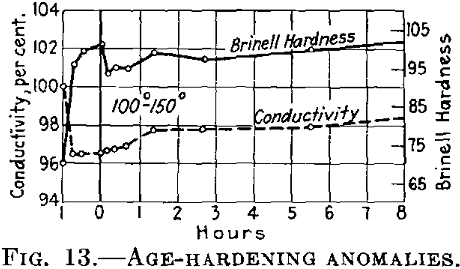
If the conditions are such that during the first treating at the lower temperature the conductivity finally becomes constant, it is at first maintained almost constant at the higher temperature (Fig. 13), while the hardness drops.
How can these phenomena be explained? G. Tammann has counted the nuclei in undercooled organic melts in the following manner. He first undercooled the melt to a low temperature at which nuclei are formed but crystal growth has not yet occurred. Then he heated it quickly to a higher temperature at which crystal growth takes place but nuclei are no longer formed. By this method he rendered the nuclei visible and by taking various low temperatures he could show the well-known curves of nuclei formation in dependence on temperature.
But M. Yolmer and N. Weber have pointed out that the minimum “critical size” of the nuclei at which they begin to be stable depends on temperature and consequently decreases with increased undercooling. Indeed, the stability jump from the supercooled liquid to the crystal increases with failing temperature and the free energy of the surface can be overcome at lower temperatures with smaller sizes of nuclei than at higher temperatures. It may therefore be expected that part of the nuclei formed at a lowrer temperature will become unstable when brought to the higher one. At this temperature only the larger nuclei will show further growth whereas the smaller ones will be remelted again.
The ideas of M. Volmer and N. Weber also relate to supersaturated solutions; for instance, to the aging of duralumin, since we can speak here also of nuclei, as we have shown above.
At the lower temperature, the size of the nuclei is small; it lies in the neighborhood of the “critical value.” The formation of these nuclei reduces the thermal movement of the atoms of copper as discussed above and it is therefore not probable that there will be an appreciable growth of the nuclei at the lower temperature. When raised to a higher temperature, these nuclei will become unstable and again be dissolved. The formation of larger nuclei starts at once. But the diffusion involved in this process is more extensive than that required for dissolving small nuclei and therefore it proceeds more slowly. The number of distorted points in the space lattice will therefore be diminished and the hardness will decrease.
But as to this explanation, the objection may be raised that a simple coagulation (change of shape) of the nuclei can have the same effect. It seems unnecessary to make such complicated assumptions for explaining these observations. Again, this objection is contradictory to the behavior of the conductivity. If the conductivity decreases owing to the aging at lower temperature, this means that it is lowered by the nuclei formation. Its rise after being heated to the higher temperature can be explained just as well by the solution of some nuclei as by their “coagulation.” But if the conductivity rises even at the lower temperature, as in Fig. 12, it is increased by the nuclei formation. The re-solution of the nuclei will therefore reduce the conductivity, but their coagulation will only accelerate its rise. The conductivity fall at the higher temperatures can only be explained by the re-solution of the nuclei in the way assumed for liquids by M. Volmer and N. Weber. If the conditions at the lower temperature are such that the conductivity is not at all changed by the nuclei formation, there is no reason why it should be changed at the higher temperature. It remains constant as in Fig. 13.
The experiments carried out by O. Dahl with silicon-nickel alloys yielded similar results. The hardness anomaly after a rapid heating to a higher temperature can thus be easily explained by the theory of nuclei formation.
It is interesting that P. Merica, without knowing the results discussed above, assumed in his lecture of 1932 in connection with this phenomenon that the molecular process started during the aging at lower temperatures must in some way be reversed at the higher temperature.
We may on the same basis account for another anomaly also discovered by W. Fraenkel. Assume that an age-hardenable alloy does not show a definite change of electrical conductivity when aged at room temperature immediately after quenching. Its conductivity drops by aging at the latter temperature if it has been aged partly at a higher temperature, say at 100° C. for aluminum alloys, and afterwards is aged at the lower temperature.
Now, although we do not know the exact cause of the decrease in electrical conductivity by aging at low temperatures, one thing seems to be sure; viz., that this drop in conductivity can be produced only by “knots” of extreme smallness and that larger nuclei, whatever their nature may be, will tend to increase the conductivity in accordance with the laws of heterogeneous equilibrium. If the aging decreases the conductivity, the “knots” formed will be, on the average, very small; if it increases the conductivity, as in duralumin at higher temperature, the nuclei on the average will be larger. If there is neither a decrease nor an increase in conductivity during aging, the smaller and the larger nuclei will be mixed in such proportions that on the average they will have no bearing on the result.
We assume that the distribution of the second metal in the mixed crystal is statistically irregular. But if we begin the aging at 100°, the formation of nuclei will proceed preferably at centers where large ones can be formed. When the aging begins later at the lower temperature, these large nuclei will remain as formed at 100° and the formation of small ones will be favored. This formation of small nuclei is accompanied by a drop in resistivity.
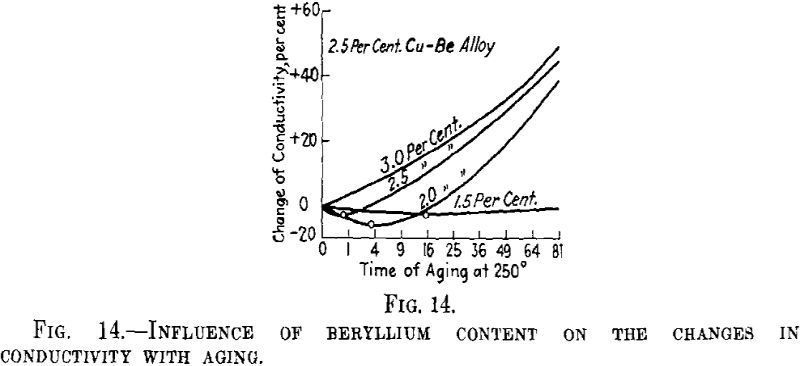
The previous aging at a higher temperature must act as a lowering of the degree of supersaturation of the mixed crystal. If the interpretation given above proves correct, the same change as that produced by the previous aging at higher temperature can be obtained for an alloy having a smaller concentration of the second metal. This has been confirmed for the alloys of copper with beryllium. Fig. 14 shows that for the alloy with 3 per cent beryllium the electrical conductivity of the thin wire investigated first increases by aging at 250° C., while in the alloy with 2.5 per cent beryllium it decreases in the first hr. of aging and in the alloy with 2 per cent beryllium in the first 4 hr. In connection with the matter discussed above, this shows that in alloys having lower contents of beryllium small nuclei predominate more than in those with higher contents of beryllium.
Thus far we have considered the formation of nuclei. We shall now discuss changes in the matrix crystal during or after the separation of
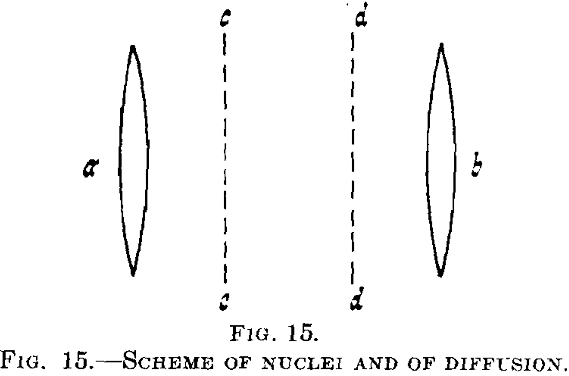
nuclei. In this, we shall confine ourselves to comparatively large nuclei formed at higher temperatures where a second crystal phase is definitely produced. During its segregation the concentration and therefore, generally speaking, the lattice constant of the supersaturated mixed crystal, is altered.
Suppose that in a supersaturated mixed crystal there are two nuclei a and b, Fig. 15, of the second phase, say of CuAl2 in a solid solution of copper in aluminum. Then the supersaturation will be eliminated in the neighborhood of a and b, whereas at greater distance, say between cc and dd, the supersaturated solution will be wholly unchanged at first. Diffusion will start between the parts richer and poorer in copper (of maximum and minimum copper content) and a continuous decrease of copper content will be developed gradually.
A continuous change of lattice constant corresponds to this decrease and on the X-ray film a broadening of the diffraction lines may be expected between the limits that correspond to the concentration at the beginning and at the end of the segregation process. This has been found true for the alloys of beryllium and duralumin, but in silver supersaturated with copper, Ageew, Hansen and Sachs have found, as is well known, that during the process of the separation of copper crystals, instead of a gradual variation of the intermediate values of the lattice constant, there are two constants, corresponding to the beginning and to the end, respectively, of the segregation process. The intermediate values are present only to a much smaller extent, so as not to be clearly marked on the X-ray patterns.
One feels inclined to assume that this indicates another segregation process involving three phases, which is fundamentally different from the ordinary process observed in duralumin. But this is not so, as the following discussion will show.
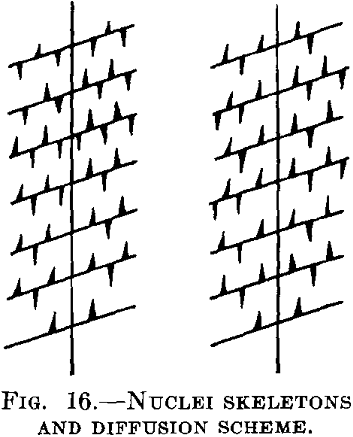
Imagine that in the supersaturated silver there are regions where the separation can proceed more easily than in others. Such regions may lie at the corners of the crystals and the separation may occur in such manner that from certain single starting points (nuclei), crystal skeletons are formed as shown in Fig. 16. The branches of these skeletons lie very close together, whereas the distances between the single skeletons, as arising from different starting points, are much larger. In such a case the concentration between the branches of the skeleton will reach the saturation limit very rapidly, while in the areas between different skeletons it may be virtually unaltered. The segregation in these intermediate spaces will proceed much more slowly, either without further nuclei formation or with the formation of a few nuclei in the shape of plates, so that the diffusion paths used by the copper atoms to reach the nuclei are, on an average, much longer than the paths between the skeleton branches. But if the conditions are such that the nuclei remain plane plates, and the segregation proceeds in accordance with Fig. 12, the unaltered value will not be observed simultaneously with one in the saturated equilibrium condition. As a whole, of course, the process will be, retarded in this case.
In copper saturated with silver, the last condition seems to be fulfilled with very large (single) crystals, and the first with fine crystals (polycrystalline material). With the single crystals the separation proceeds much more slowly than in the other case. It seems therefore that with these conditions grain boundaries act as starting points for the formation of skeletons.
The scheme given above also explains the other very striking observation made by Ageew, Hansen and Sachs, to the effect that a mixed crystal with segregated copper that has been cooled slowly from high temperatures again shows two distinct values of the lattice constant when reheated for a short time to a high temperature. In the neighborhood of the “nuclei” the branches of the skeletons evidently lie much closer to one another than in the intermediate regions, and the re-solution of the segregated copper is in the first case greatly accelerated in comparison with the second case.
These considerations on age-hardening may well be terminated with the following general remark. The process of aging and associated phenomena clearly shows, on the one hand, that a theoretical discussion of the problems involved offers great difficulties, since for the most part only qualitative statements are available and, on the other hand, that under these circumstances many contradictory results can be derived from the same theoretical basis, so that one must be very cautious in the introduction of new fundamental hypotheses in this field.
