Table of Contents
Gravity concentration is a general term designating processes for separating and sorting granular material by means of forces that depend on the density, size and shape of the particles. When these forces are applied to the particles the latter are caused to move, those of a given density along one path and those of a different density along another, until ultimately they are sufficiently separated to be removed from the operation of the process.
The forces producing this separation are in general complex and, unfortunately, no completely rigorous analysis of them has as yet been devised. The science of the hydrodynamics of viscous fluids deals with the little that is known about the problem.
Motion of a Particle in a Viscous Fluid
One of the physical problems with which gravity concentration is most concerned is that of determining the resistance encountered by a particle moving through a fluid. This problem has a curious history and a great deal of attention has been given to it by theoretical physicists. The special case of a particle of spherical form was investigated by Newton and Stokes. Newton arrived at the conclusion that the force would vary as the square of the velocity. Stokes analysis, on the contrary, shows that the force will be proportional to the first power of the velocity. Modern research has shown that neither is correct over the entire range of conditions of particle size, velocities and fluid viscosity. For small spheres moving at slow speeds, Stokes law has been verified experimentally. Large spheres with rapid movement follow Newton’s law more nearly. Spheres of intermediate size follow a compromise relationship, which has been variously expressed by different investigators—notably by Rittinger.
Stokes’ law, which applies to cases of laminar flow or where the resistance is due to viscosity, states that the resistance to the motion of a sphere moving in a fluid is
F = 6πµrυ…………………………………………………………………………[1]
where µ is the coefficient of viscosity, r the radius of the sphere and v the velocity. This relation has been shown experimentally to hold quite accurately for small spheres moving at low velocities.
m dv/dt = mg – 4/3 πr³ρg – F………………………………………………………….[2]
Substituting the value of F from Stokes’ law and the volume of the sphere times its density Δ for m, this equation becomes
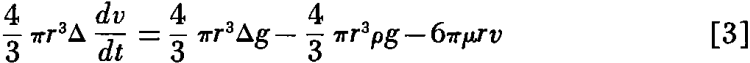
which when solved for dv/dt the acceleration, gives

It is found that vt, the terminal velocity, is

This equation is applicable only to a particle that falls in accordance with Stokes’ law. Newton, on the other hand, calculated the resistance to the motion of a sphere as
F = π/2 pr²v²………………………………………………………………….[6]
F = Q π/2 pr²v²………………………………………………………………………..[7]
which is commonly referred to as Rittinger’s equation.
The terminal velocity of particles settling in accordance with Newton’s or Rittinger’s law may be found in a way similar to that used for Stokes’ law.
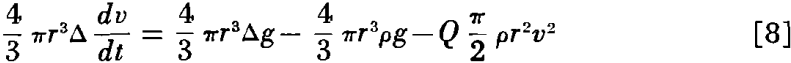
which on solving for dv/dt becomes
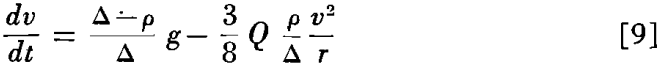
Setting this expression equal to zero as before and solving for vt
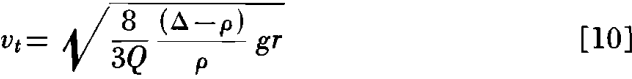
This equation gives the terminal or maximum velocity of a particle falling in accordance with Newton’s law as modified by the introduction of the coefficient of resistance Q.
Physical relationships are commonly expressed as mathematical functions of various quantities, all of which may be reduced to simple ratios of fundamental multiples of units of length, mass and time, or their equivalents. Any such expression must be dimensionally homogeneous; that is, the terms in a sum must have the same units or dimensions. This is merely a statement of the fact that it is unlikely that a useful result will be obtained by adding inches to pounds or any other dissimilar quantity.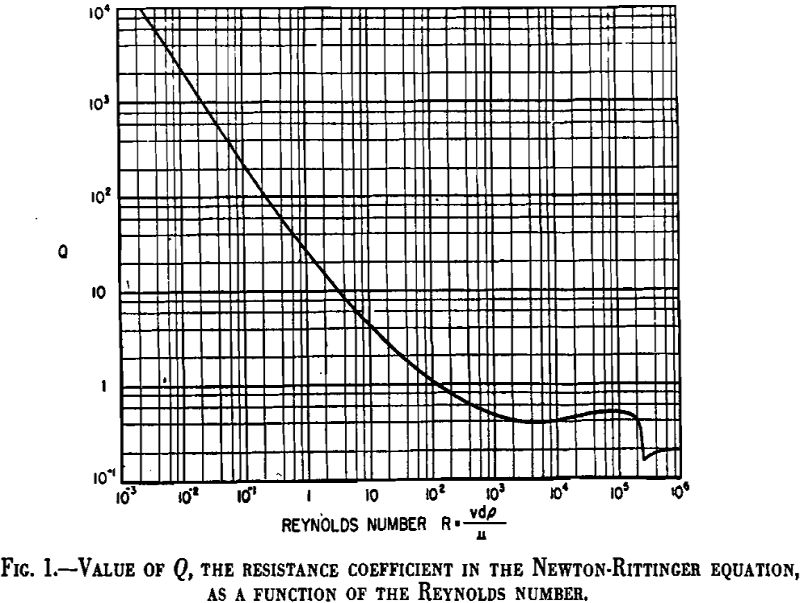
In Stokes’ law the force of resistance is proportional to v and Q, consequently, will be inversely proportional to v and will be represented by a straight line of slope — 1. This is actually the case for low Reynolds numbers as shown.
Hindered Settling
The foregoing discussion of the motion of spheres falling freely in a fluid represents the simplest case of the principal problem of gravity concentration. Unfortunately, it also marks almost the limit of useful analysis of the problem. If the particles are not spherical in shape, if they move too rapidly or if one is close enough to affect another’s motion, the problem becomes so complex as to defy rigorous analysis. Nevertheless some progress can be made toward at least a qualitative understanding of the behavior of
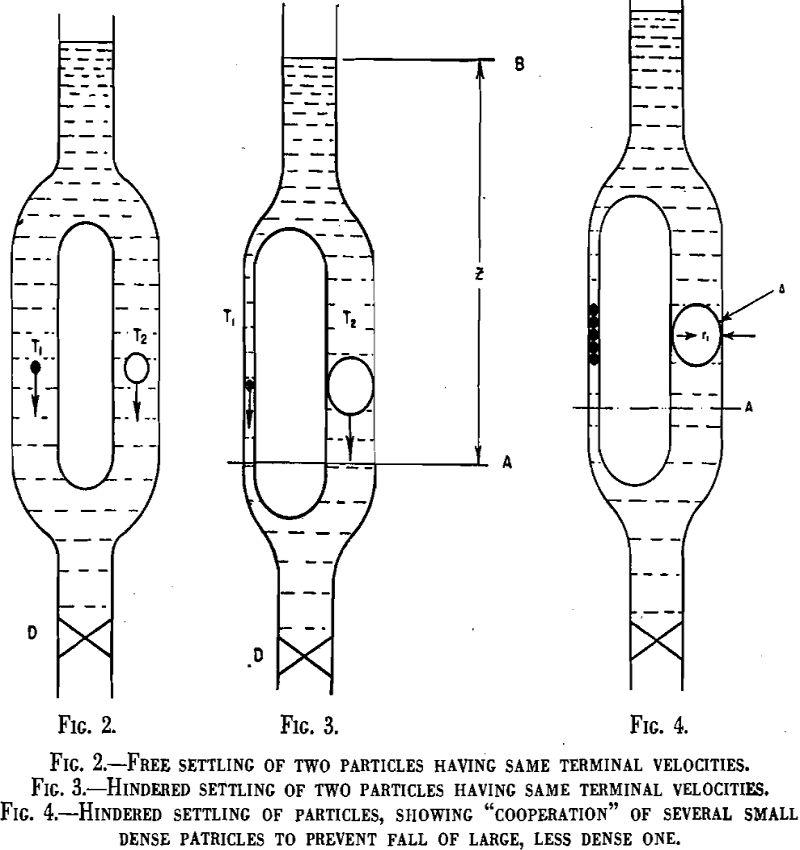
particles moving under conditions of hindered settling. Many of the conclusions will be reached intuitively and will be nothing more than approximations; they may, however, be useful.
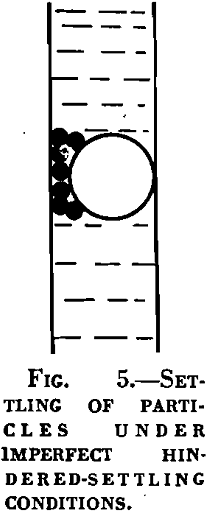
One other principle of hindered settling seems to be well established. This principle may be stated as follows: Any particle of a size comparable to the other particles in a suspension of solids in a fluid behaves as though it were immersed in a medium having a density equal to the mean density of the suspension in the vicinity. In other words, a suspension of solids in a fluid behaves as though it were a liquid having a density equal to the mass of the suspension divided by its volume, and a particle immersed in the suspension is buoyed up in accordance with Archimedes’ law. This fact is verified by experiment for particles as large or larger than those composing the rest of the suspension. It is easily proved analytically by the following considerations:
Classification
Classification as applied to coal washing is the process of separating particles of various sizes, densities, and shapes by allowing them to settle in a fluid.
As far as the theory of the process is concerned, it is immaterial whether the particles settle in the fluid or the fluid rises among the particles. As a practical matter, however, it is apparent that the details of the separation will depend on the physical arrangements of screen plates, draws, overflows, etc. The tube classifier is an example of the classifier in its simplest form
In an actual experiment a 1¾-in. tube classifier was charged with 300 grams of rounded silica sand sized carefully to —20+24 mesh. The average mass and volume of a single particle were determined by actual count of a gram of the sand and were found to be 0.00066 gram and 0.00025 c.c., respectively. The terminal velocity of the average particle was found to be 11 cm. per second. The value of σ is 1 for water using the value of Fv determined to be 0.235 at V=3 cm. per sec., the following comparison of the densities with values calculated from 45 was obtained:
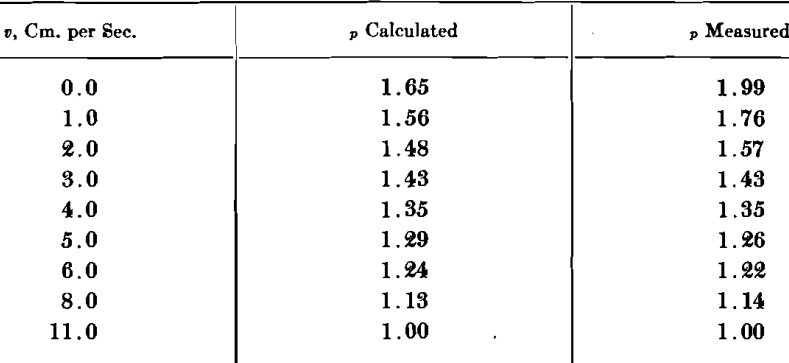
That large particles respond to a suspension as though it were a fluid having the mean density of the suspension is easily shown by placing a hydrometer in a suspension of fine particles. The form of Eq. 45 and its agreement with experimental evidence for the special case of sized material would seem to indicate that this principle is also true with particles of a size about equal to those composing such a suspension.
Oscillation Principle
The statement that it is desirable to operate a gravity concentration process with as dense a bed as possible is not an absolute law. It is very evident that if followed to its logical conclusion it would lead to a condition where particles would be so interlocked that no separation at all would be possible. It is necessary to stop short of maximum density in order to achieve a separation.
At this point we are on uncertain ground and our reasoning must be intuitive. As a guide, it will be well to call to mind some of the factors that are important in a commercial gravity-concentration process. Of obvious importance are the completeness of separation and the rate of separation or capacity of the machine or process. It may be concluded that the completeness of separation will depend on the maintenance of a bed of maximum density, or, as it is sometimes called, a condition of maximum hindered settling. On the other hand, rate of separation or the capacity of the process or machine will depend on the freedom of movement of the particles in the bed. This condition is commonly referred to as “mobility.” Thus it is evident that an operating gravity concentration process represents a compromise between conditions of maximum bed density and mobility, the compromise being chosen so as to obtain a desired completeness of separation at an acceptable capacity.
Dense-Medium Processes
Dense-medium processes are the simplest of all gravity concentration methods. Where the fluid itself is of intermediate density to the materials to be separated, it is evident that the force acting on a dense particle will be directed downward, while that on a light one will be upward. Processes using liquids of high density—such as carbon tetrachloride, calcium chloride and zinc chloride solutions, acetylene tetrabromide, Clerici’s solution, a mixture of thallium malonate and formate, and similar heavy liquids—form the basis of the float-and-sink method of testing and analyzing ores. In recent years the use of additional materials to prevent the liquids from wetting the ore, thus avoiding loss of the liquid, has made it possible to use relatively expensive heavy liquids commercially.
Jigging
Jigging is one of the most ancient of ore-dressing methods, but in spite of the vast amount of study that has been given to the process it is not very well understood. To determine what happens in a jig bed during a complete cycle of pulsation, settling and possible suction phases, a careful study has been made at Battelle Memorial Institute in connection with a theoretical study of jigging processes.
An obviously important variable in the cycle is the upward velocity of the fluid passing through the screen plate. For simplicity, we will consider the graph of a cycle in which this velocity varies with the sine or cosine of the time. The sine curve is typical of many jigging operations, though recent research has shown that it is not the best possible cycle. The sine wave is commonly superimposed on a constant velocity produced by a steady input of water to the jig, the effect of which is simply to raise the curve relative to the time axis. Such a curve, somewhat idealized, is shown in Fig. 8. Important events occurring during the cycle are also shown.
Launders
Launders, in principle at least, represent an ideal method of gravity concentration. In theory the bed density in a launder stream increases from the top to the bottom, a desirable condition from the standpoint of selectivity in the separation. The mobility decreases with depth. If heavy material is withdrawn from the bottom of a flowing stream, it is evident that it will at some time have passed through a zone where the bed density is as high and the mobility as low as practicable—a condition already recognized as most desirable in gravity concentration processes. Launders have the additional advantage of requiring a minimum number of moving parts in their construction.
Shaking Tables
Shaking tables introduce no principles of separation that have not been considered. The sequence of hindered settling followed by flowing stream selection is frequently utilized by submitting material to be concentrated to a preliminary classification. This is so common a practice that classification and tabling has almost come to be recognized as a unitary process.
Particles in a bed of material on a shaking table are subjected to the action of hindered settling in the way already discussed. A differential motion of the table suffices to cause heavy-gravity material to move along the table between riffles, if these are present, while a cross stream carries low-gravity material transversely.
