Multi-timbered Wood Crib Supports

Wood cribs are used extensively by the coal mining industry in a variety of applications to stabilize mine openings. The U.S. Bureau of Mines is conducting research to evaluate the load-displacement characteristics of active and passive mine roof support systems, such as wood cribbing, so that the selection and design of these supports are compatible with the conditions in which they are employed.

A cooperative effort was undertaken by the U.S. Bureau of Mines with the Cape Breton Development Corp. (CBDC) Sydney, Nova Scotia and the Cape Breton Coal Research Laboratory (CBCRL), Sydney, Nova Scotia to evaluate the behavior of gate side packing materials used in advancing longwall mining applications in the Sydney Coalfield. As part of this effort, full-scale tests were conducted on wood pack wall supports in the Bureau’s 3-million lb (13.3 MN) active load frame. Gate roads constructed behind an advancing longwall face are supported on one side by a continuous coal pillar and on the side nearest the extracted panel by some form of artificial support, typically referred to as the gate side pack wall. In addition to providing resistance to gate road convergence to maintain entry stability, the gate side pack must also serve as a barrier against gob debris.

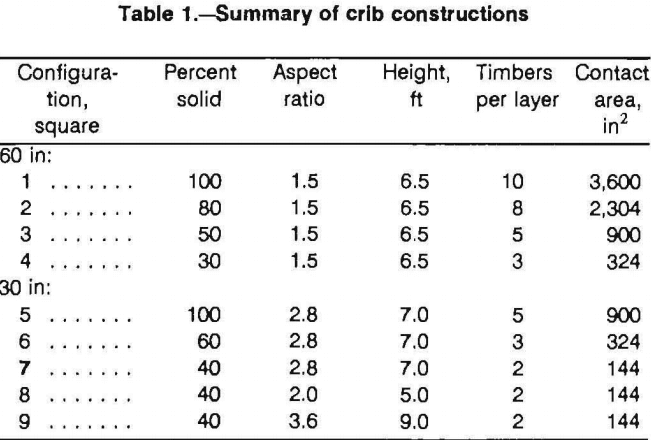
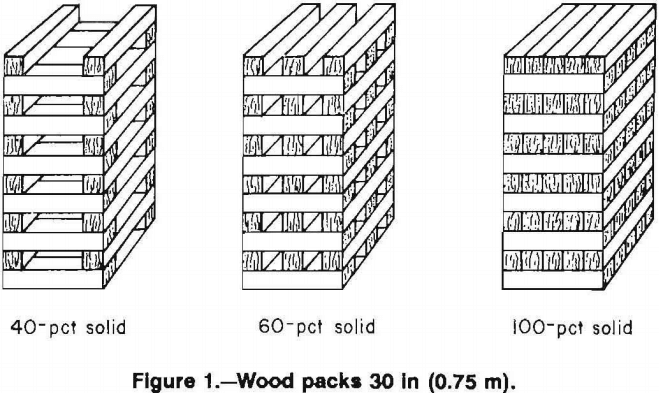
Nine different pack configurations were evaluated as part of this study. The wood pack wall supports were multitimbered crib constructions from 6-in (0.15-m) by 6 in (0.15-m) cross section timbers using timbers 30-in (0.75-m) and 60-in (1.5-m) in length. The percentage of solid material in the crib constructions varied as shown in figures 1 and 2. A summary of crib constructions is provided in table 1.

In summary, this report describes generalized wood crib performance and reports the results of full-scale tests of several wood pack wall configurations that are being employed in advancing longwall operations in Canada.

Generalized Wood Crib Behavior

Generalized wood crib behavior is described to provide a basic understanding of the loading and failure mechanics essential to the design and evaluation of wood crib supports. These observations are based upon tests conducted on wood pack wall specimens in cooperation with CBCRL and other independent Bureau studies.

Compression Characteristics

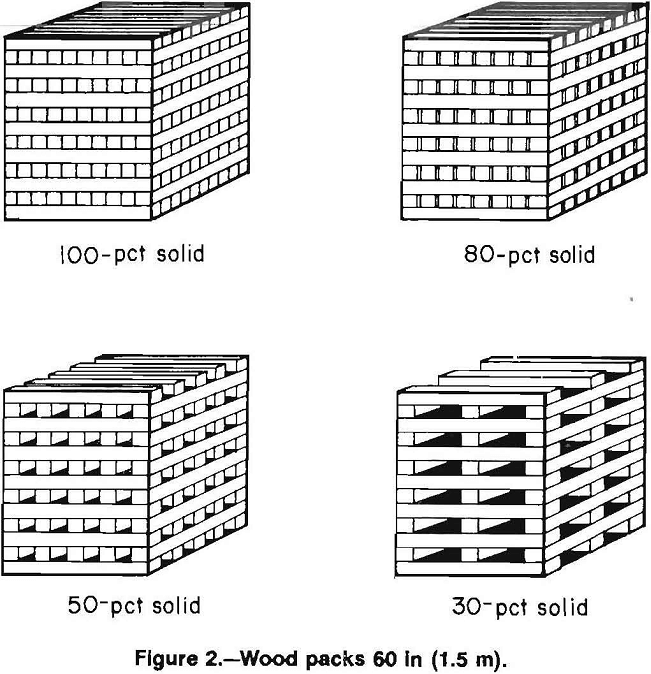
The resistance-to-convergence relationship for a wood crib support follows a distinct pattern as shown in figure 3. Two regions of linear or proportional behavior are followed by a nonlinear load rate. Well constructed cribs from consistent good quality wood should be able to converge from 35 to 40 pct of their height prior to reaching ultimate strength. However, the ultimate load-bearing capacity is often reduced from premature failure caused by buckling of the structure or localized failure of individual crib timbers.

Initially, the resisting force of a wood crib increases quickly at a uniform rate and is termed the linear elastic deformation phase. This deformation phase typically occurs during the initial 5 to 10 pct of crib deformation. The ratio of force-to-convergence or resistance rate then decreases to another uniform rate, which is characterized as linear plastic deformation. Plastic deformation may occur up to 25 or 30 pct of overall crib deformation. In this region, the crib undergoes considerable deformation while producing significantly less resistance. Finally, the rate of resistance increases nonuniformly and is identified as the nonlinear plastic deformation phase. This typically occurs after 25-pct crib deformation. This region is most likely where cellular structure of the wood has collapsed and the ultimate strength of the crib is realized.

Buckling Characteristics

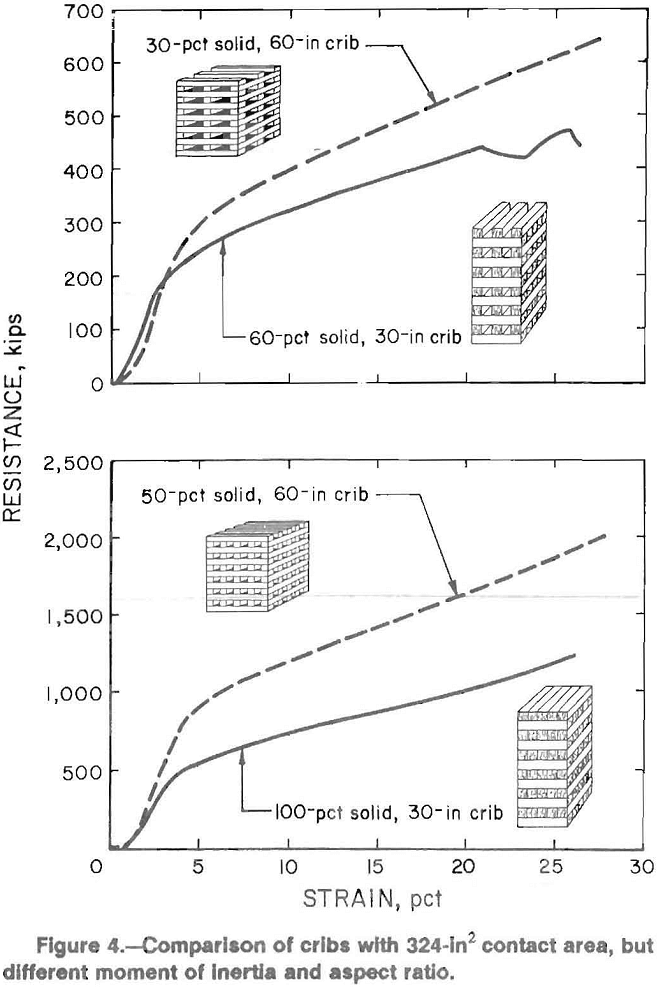
In general, buckling reduces the stability and load capacity of the crib, and can occur in any phase of deformation. The occurrence and nature of buckling effects are primarily dependent on the structural moment of inertia and effective column length. In relationship to wood crib structures, the moment of inertia is a function of the crib width and contact area among timbers, and the column effective length is a function of the crib height and end conditions. Moment of inertia is governed by the amount of contact area and position of the contact area within the structure. Figure 4 compares cribs with the same contact area, but different widths. An increase in width increases the moment of inertia given the same contact area, and results in higher crib capacities.

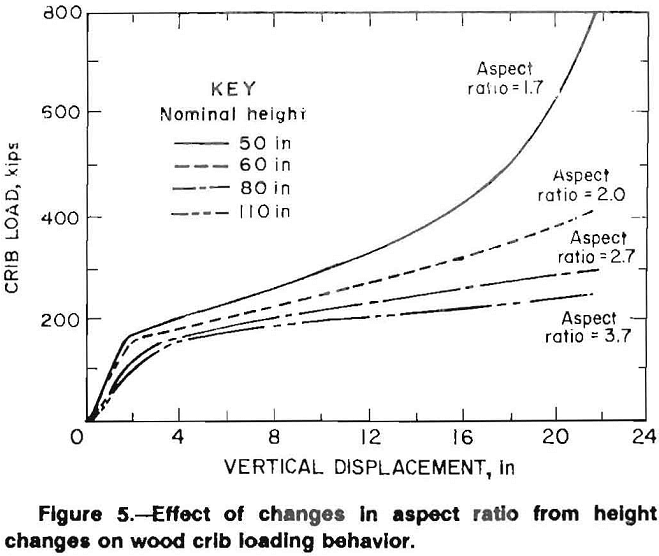
The buckling effects related to crib height may also be defined in terms of the crib aspect ratio. Unlike the moment of inertia, the aspect ratio does not consider the amount or position of the contact area. Buckling effects become more prevalent and severe as the aspect ratio increases. Figure 5 shows the effect of the aspect ratio, which varies from 1.7 to 3.7. The cribs in this comparison have the same moment of inertia and width, and vary only in height.

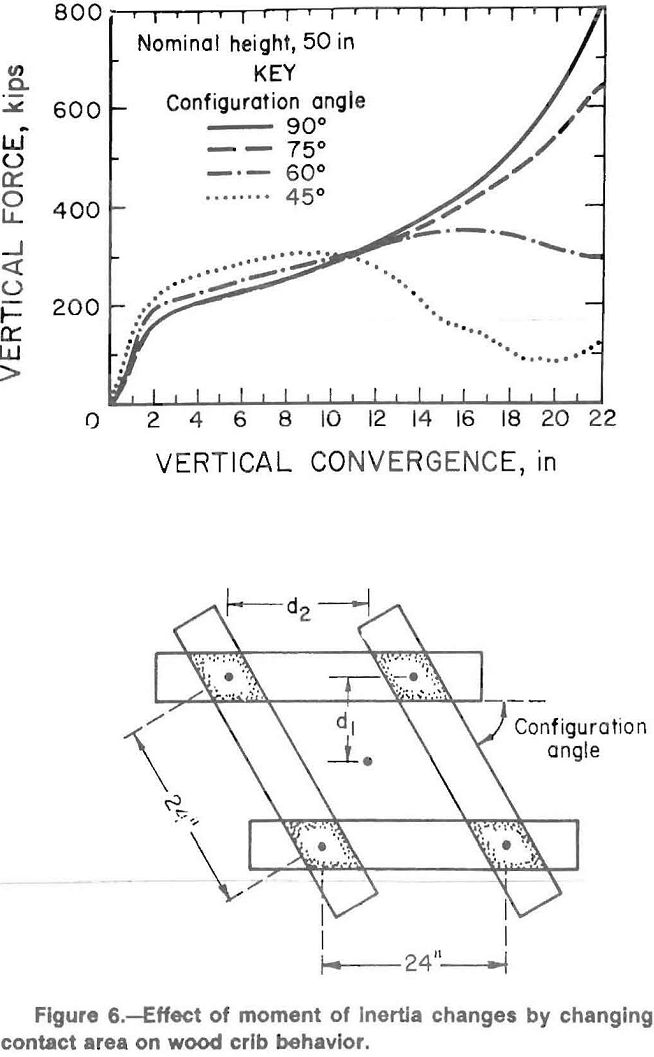
Buckling occurs in the direction of the minimum moment of inertia for the structure. Hence, a crib with a plan view of 3-ft (0.9-m) by 6-ft (1.8-m) is no more stable against buckling than a 3-ft (0.9-m) by 3-ft (0.9-m) crib. Figure 6 shows the effect of reducing the moment of inertia by changing the contact geometry of the crib layers for two layer construction. The contact area is increased, however the moment of inertia is decreased. In summary, increasing the moment of inertia or decreasing the aspect ratio results in an apparent increase in crib resistance due to a decrease in buckling effects.

Localized Behavior Characteristics

The overall performance of a wood crib can be significantly affected by localized behavior of one timber within the crib. If the strength of individual timbers in a specific layer varies significantly, then the layer compresses unevenly and the crib is more susceptible to the effects of buckling. The compressive properties of wood are significantly dependent on the moisture content of the wood. Tests on individual maple species show that the compressive strength increases from 70 to 150 pct as the wood seasons. A comparison of a variety of maple species shows that the compressive strength can vary by as much as 300 pct between green wood (moisture content greater than 30 pct) and seasoned wood (moisture content 12 pct). Therefore, it is important to construct wood cribs from timbers of the same type of wood or wood with the same physical properties to minimize the effects of localized behavior.

Overall, crib performance is also affected by localized failure, which is the failure of one timber within the crib. Figure 7 shows the failure of an individual timber due to shear causing a reduction in overall crib capacity. When one timber fails, the crib capacity can be maintained by other timbers in the same layer and adjacent layers. Therefore, crib layers constructed from multiple timbers are less susceptible to local behavior, since load is distributed to several timbers. Likewise, in multitimbered constructions, timbers furthest from the center contribute most to the moment of inertia. Hence, consideration should be given to placement of the best timber specimens at the outer most distance from the crib center in multitimbered constructions if timber quality is inconsistent.

Bureau studies have shown that the local behavior can be controlled and the effects reduced by allowing timberends to overhang adjacent timbers as shown in figure 8. This is particularly critical to cribs constructed with two timbers per layer, since there are fewer timbers to redistribute the load. The overhanging timbers compress and interlock, which prevents timbers from rolling or sliding out of place. The interlocking configuration also confines the timbers, which increases compressive strength and reduces susceptibility to the type of shear failure shown in figure 7.

Stiffness Characteristics

The slope of the curve representing the force-to-convergence relationship is equivalent to the crib stiffness, therefore the two linear portions of the curve (fig. 3) can be described as the elastic and plastic stiffness of the crib. Tests have shown that the ratio of elastic to plastic stiffness is a constant for cribs constructed of the same wood type and is independent of crib height, moment of inertia, and wood moisture content. The magnitude of the elastic and plastic stiffnesses are dependent on contact area and height. Stiffness increases linearly with contact area, and increases exponentially as height decreases.

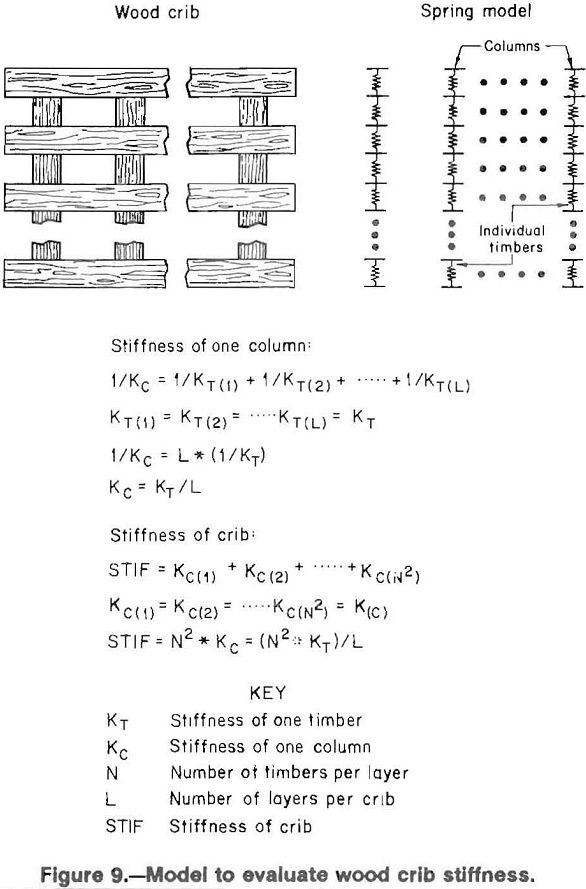
The Bureau is currently working on a model to predict overall crib stiffness for specific crib constructions based upon the stiffness characteristics of individual crib timbers. The model is shown in figure 9. The model requires stiffness of an individual timber, to determine the stiffness of the overall crib. Each point of contact within a crib is modeled in series with other layers as an individual column. The stiffness of the columns are then modeled in parallel to obtain the overall crib stiffness. The number of columns is equivalent to the number of contact points in a layer, and is equal to the square of the number of timbers per layer.

Load Rate Characteristics

Since wood is a visco-elastic material, the overall behavior and load capacity of a crib is affected by the rate at which load is applied. At slow strain rates, failure within the wood microstructure occurs at a rate that allows stress to be relieved through natural crack propagation. As the strain rate increases, natural crack growth occurs too slowly to relieve stress within the wood material. The result is an increase in the stress per unit strain, which is seen as an increase in crib stiffness. Tests conducted by the Bureau revealed that load rate effects diminish considerably for load rates greater than 0.1 in/min (0.25 cm/min). As a result, the Bureau uses 0.5 in/min (1.27 cm/min) as a standard load rate for wood crib tests.

Wood Pack Wall Test Results

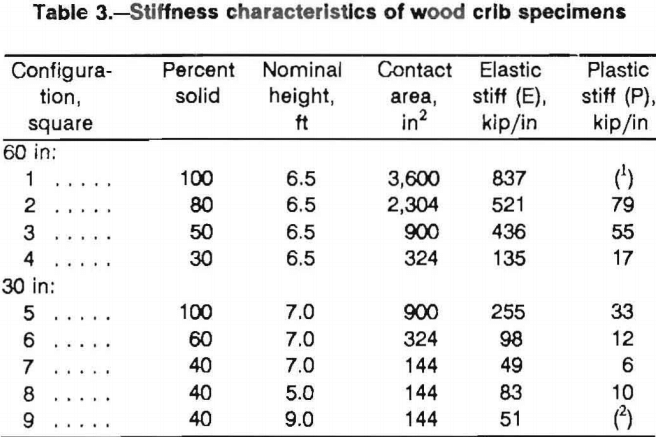
The nine configurations described in table 1 and shown in figures 1 and 2 were tested under controlled displacement at a rate of 0.5 in/min (1.27 cm/min) in the Bureau’s mine roof simulator (MRS). Tests were terminated upon reaching the 3 million lb (13.3 MN) capacity of the simulator or the 22-in (0.56-m) stroke limit. The results of the tests are presented in tables 2 and 3 and figure 10. As expected, stiffness and crib resistance increased with increased contact area as shown in figure 10A for cribs constructed from 30-in (0.75-m) timbers and in figure 10B for cribs constructed from 60-in (1.5-m) timbers.

Crib Deformation Analysis

All 30-in (0.75-m) configurations converged to the full 22-in (0.56-m) stroke of the simulator without reaching ultimate strength providing a deformation capability in excess of 25 pct. The 100- and 80-pct solid 60-in (1.5-m) crib configurations reached the 3 million lb (13.3 MN) load capacity of the simulator, while the 30- and 50-pct solid configurations maintained load for the full 22 in (0.56 m) of convergence. The 30-, 50-, and 80-pct solid 60-in (1.5-m) configurations and the 100 pct solid 30-in (0.75-m) configuration maintained plastic deformation into the nonlinear phase.

Figure 10 shows the deformation characteristics for the 30- and 60-in configurations. An evaluation of the deformation phases with respect to convergence was investigated and provided some relationships. The amount of convergence in the elastic deformation phase is not affected by configuration percentage of solid material, and appears to be only affected by the height of the crib. The convergence range for the elastic-plastic transition phase appears to increase with the percentage of solid for the 60-in configurations, but the same trend was not evident in the 30-in configurations. This may be due to buckling effects as the 60-in configurations are less susceptible to buckling; however, further studies are needed to confirm a more definite relationship. Also, the start of the plastic deformation phase was fairly consistent for all configurations that achieved this phase of deformation, and the beginning of the nonelastic deformation generally began at about 14 to 15 in of displacement.

Stiffness Characteristics

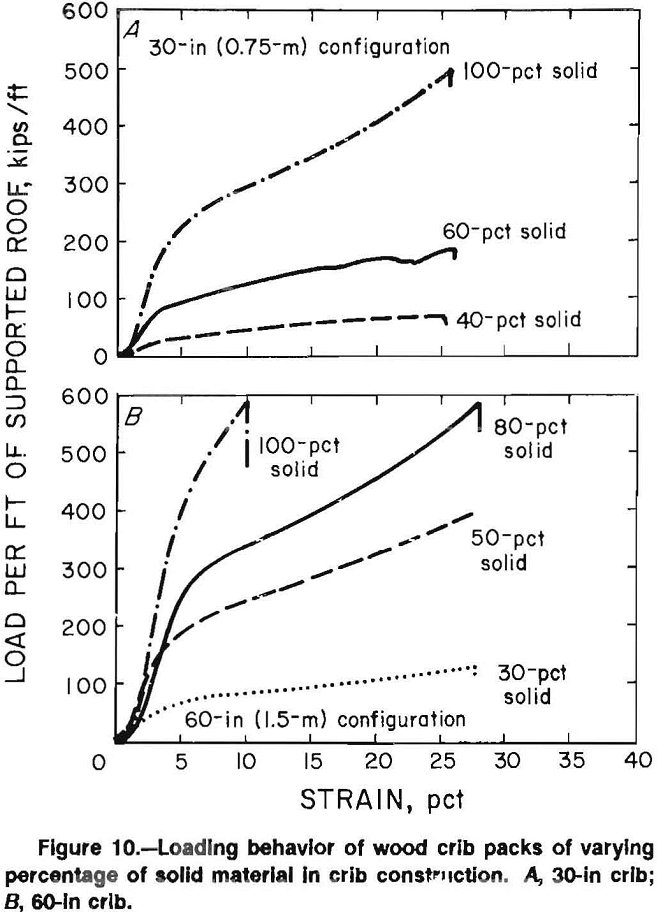
Table 3 documents the elastic and plastic stiffness for each crib configuration. As previously indicated, the stiffness increased in proportion to the increase in contact area and the percentage of solid material. Elastic stiffness ranged from 135 to 837 kips/in (24 to 147 MN/m) for the 60-in (1.5-m) crib configurations and 49 to 255 kips/in (9 to 45 MN/m) for the 30-in (0.75-m) crib configurations. Plastic stiffness ranged from 17 to 120 kips/in (3 to 21 MN/m) for the 60-in (1.5-m) crib configurations and 6 to 33 kips/in (1 to 6 MN/m) for the 30-in (0.75-m) crib configurations.

The average ratio of elastic to plastic stiffness was around 7.8 as shown in figure 11 for all crib configurations that achieved linear plastic deformation, except the 80-pct solid 60-in configuration, which was slightly lower than the others. This comparison shows that although the magnitude of the stiffnesses, and therefore the load capacities of the various configurations varied as a function of moment of inertia, contact area, aspect ratio, and height; the ratio of elastic stiffness to plastic stiffness was not affected by these parameters. Configurations with the same contact area showed that the 60-in (1.5-m) configurations exhibited higher load capacity than the 30-in (0.75-m) configurations since the moment of inertia reduced buckling effects.

Energy Absorption

Energy is an important parameter when interpreting passive roof support performance because it provides an overall relationship of capacity to force, convergence, and specimen stiffness. Energy absorption capabilities of the wood pack wall supports are consistent with deformation analysis and stiffness characteristics previously discussed.

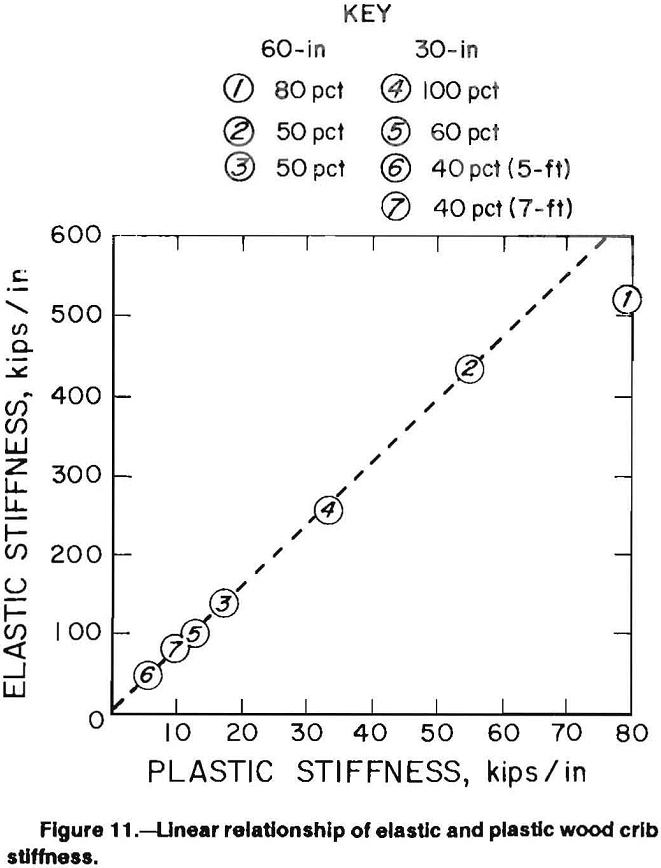
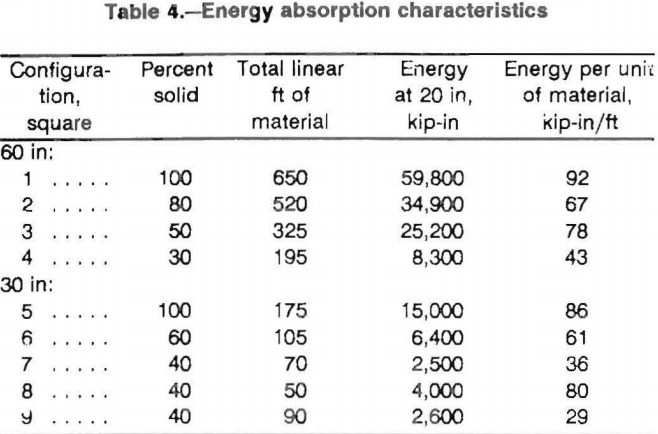
The more material in the crib, the more energy the crib can absorb. There also appears to be a trend that the higher percent solid configurations can absorb more energy per unit of material (table 4). This suggests that multitimber configurations provide a more efficient design.

Cost Benefit Analysis

Table 5 provides a comparison of crib costs per unit height of crib, costs per linear unit of supported roof, and crib resistance per construction cost, for each of the nine crib configurations. These costs are made on the basis that the 30-in (0.75) timbers cost $3.12 each and the 60-in (1.5-m) timbers cost $7.01 each.

Test results indicated that the 30-in (0.75-m), 100-pct solid configuration has almost twice the capacity as the 60 in (1.5-m), 30-pct solid configuration. The 30-in (0.75 m) configuration costs $31.20 per foot height of crib, while the 60-in (1.5-m) configuration costs $42.06 per foot height of crib. Therefore, the 30-in configuration provides twice the capacity at a 35-pct cost savings, which translates into a $7,600 saving for every 100 cribs constructed at 7-ft heights. On a cost per foot of supported roof basis, the 30-in (0.75-m) configuration provides 3.77 times the resistance per foot of supported roof at only 1.6 times the cost.

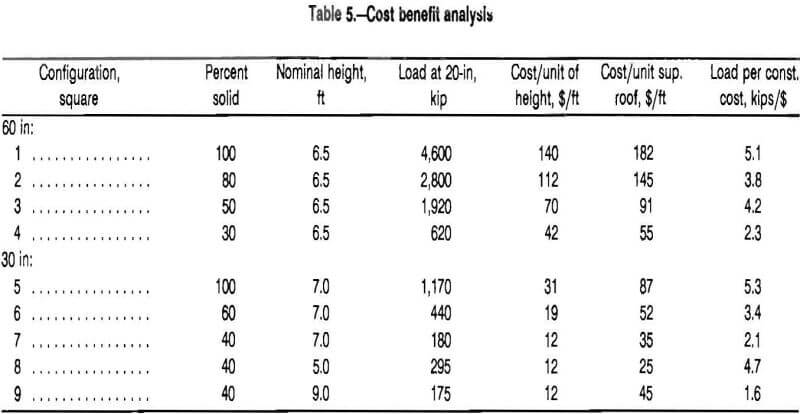
Figure 12 describes the relationship between cost per foot of supported roof and crib resistance per linear foot of supported roof as a function of the percentage of solid material used in the crib construction for 30-in (0.75-m) and 60-in (1.5-m) configurations. Figure 12A can be used to select which configuration (percentage of solid material) is needed to provide the desired load resistance per foot of supported roof. Then figure 12B can be used to optimize crib selection based on cost. For example, suppose 300 kips of resistance per linear foot of supported roof was desired. Using figure 12A, it is seen that the minimum percent of solid material is 80 pct for cribs constructed from 30-in timbers and 50 pct for cribs constructed from 60-in timbers. Then using figure 12B, it is seen that the expense of employing the 50-pct solid, 60-in crib is approximately $91 per foot of supported roof while the 80 pct solid, 30-in crib constructions would cost only $63 per foot of supported roof.

A similar cost benefit analysis can be made on the basis of supported area governed by the outside dimensions of the crib. The 30-in square configurations provide 6.25 ft² of roof support while the 60-in square configurations provide 25 ft² of roof support. This ratio of the areas of supported roof (25/6.25 = 4) is the same as the ratio of the contact area for cribs with the same percent material construction. For example, the 100-pct solid, 60-in configuration has 3,600 in² of contact between timbers while the 100-pct solid, 30-in configuration has 900 in² of contact. Since the load capacity of the crib increases in proportion to the contact area between timbers, the 30- and 60-in configurations with equal percentage of wood in the construction provide about the same resistance per square foot of supported roof as shown in figure 13A. Likewise, the construction costs are similar as shown in figure 13B

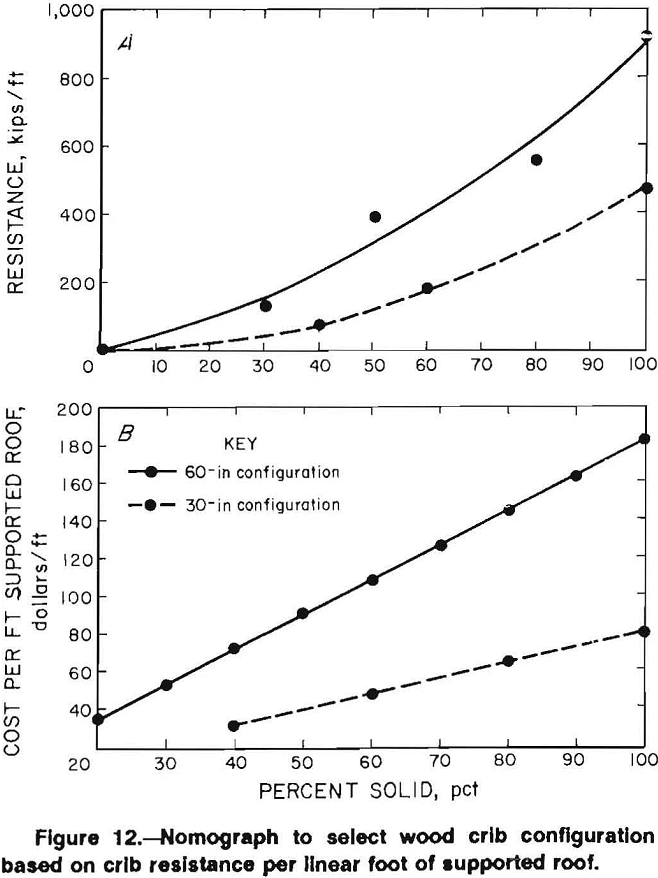
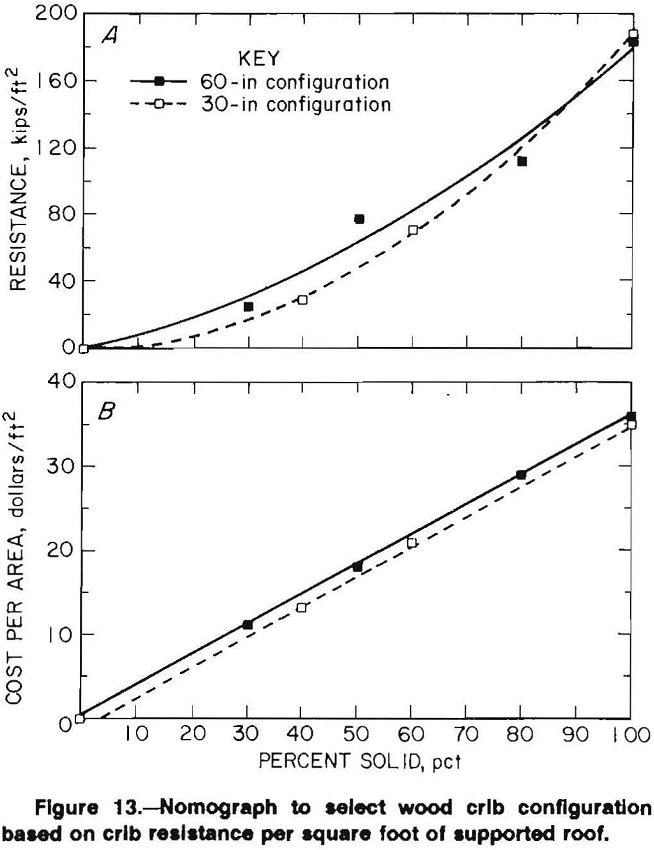
since the 60-in configuration requires twice the number of timbers which are approximately twice the cost of the 30-in timber. Therefore, strictly on the basis of resistance per square foot of supported roof, there is no cost benefit in selecting a 30-in construction over a 60-in construction or vice versa.

These examples are intended to show the types of analyses that can be conducted to select the most efficient crib design. While it is anticipated that many of these relationships will be similar for other crib constructions, some care must be made in extrapolating these analyses to other crib designs that were not tested.

Underground Observations

In situ observations of pack behavior for the configurations evaluated in the simulator were conducted by CBCRL. A comparison of in situ approximations of force-to-convergence behavior and the simulator test results are illustrated in figure 14. At first impression, it appears that the laboratory tests did not accurately simulate underground loading conditions. In general, all in situ observations suggest less loading capacity than that observed in the laboratory.

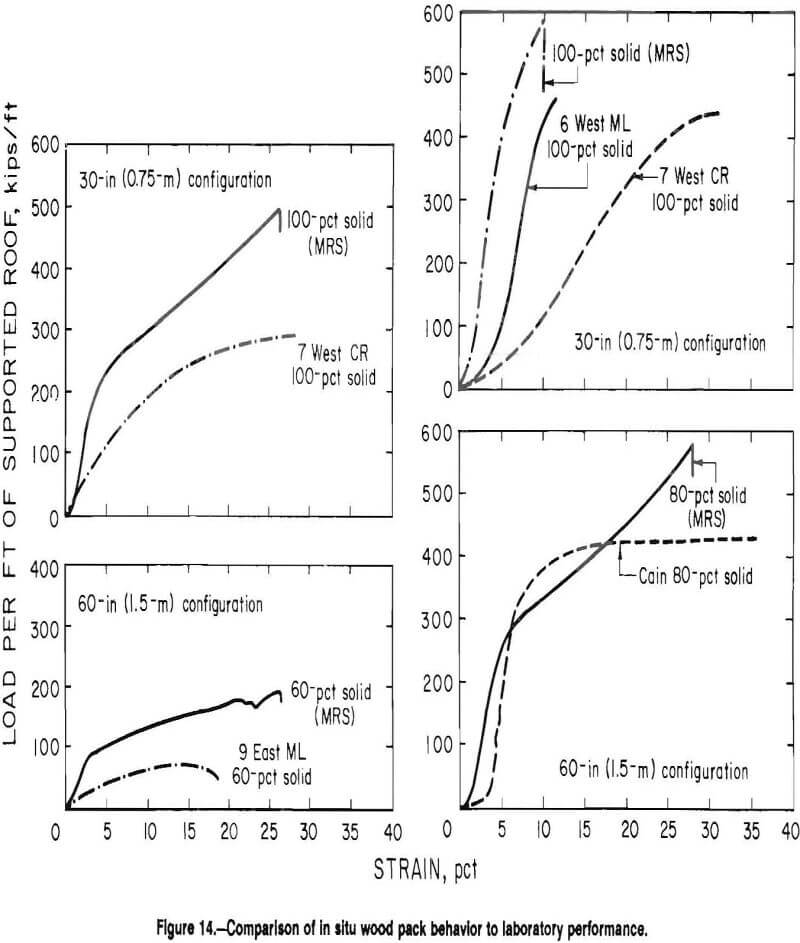
Several factors that will cause in situ behavior to differ from laboratory behavior are discussed.

1. Laboratory results are based on direct pack strain (crib displacement), while roof-to-floor closure next to the pack was measured underground. Actual pack convergence is likely to be less than observed roof-to-floor closure in soft floor or weak immediate roof conditions. Fill material added at the top of the crib to establish contact may also be less stiff than the crib structure and contribute to erroneous assessment of crib convergence from roof to floor closure measurements. This would result in an apparent reduction in crib stiffness and hence less resistance per unit deformation. The fill material may also enhance buckling effects and reduce the effective crib capacity.
2. As previously stated, the rate at which load is applied will effect crib stiffness and performance. The simulator tests applied a constant and uniform convergence load on the cribs. Underground the load is not constant or uniform, and typically occurs at a much slower rate. The slow rate allows stresses to relieve naturally within the wood. As a result, the stiffness and associated resistance is lower.
3. In situ measurements of pack load are also likely to be a source of error. Pack loading was measured by the placement of hydraulic flatjacks within the crib structure. Flatjacks measure force relative to the stiffness of the flatjack. This stiffness is affected by the contact of surrounding material, which produces errors in the measured force magnitudes. Also, the incorporation of flatjacks in the crib can affect crib stiffness and alter load transfer mechanics of the crib.
4. Laboratory tests in the stiff load frame provide a relatively uniform load normal to the packs. These boundary conditions are intended to provide optimum crib performance. Actual underground closure is rarely perfectly normal to the crib which increases buckling effects. Uneven surfaces at the mine roof and floor interface are likely to produce areas of high stress concentration and additional moment loads which alter the load transfer mechanics of the crib. While wood cribs are able to adapt to these varying boundary conditions quite well, overall crib performance will be affected.
5. Finally, it is assumed that the crib constructions were equivalent to those tested in the laboratory. Localized failure of specific timbers may reduce the performance of observed underground cribs from those observed in the laboratory, where more care was taken to avoid the use of poor quality timber specimens.

Conclusions

Wood crib supports are an important element in ground control in underground coal mining. Several factors should be considered in the design and application of these supports. Generalized wood crib behavior and results of full scale tests on wood pack wall supports are summarized as follows:

1. Wood cribs exhibit a distinct loading profile that provides definition of crib resistance as a function of convergence.
2. Load bearing capability is proportional to the contact area among intersecting crib layers. Since contact area increases with the square of the number of timbers per layer, crib performance and efficiency improve dramatically as the number of timbers per layer increases.
3. Optimum load bearing capability is likely to be reduced from buckling effects or localized failure of individual crib timbers. Decreasing the aspect ratio (height-to-width ratio) and increasing the moment of inertia will minimize buckling effects and enhance crib resistance. Wood cribs should be constructed from the same wood type seasoned to a similar moisture content to minimize the differential compression of individual timbers that promotes buckling of the crib structure. Crib performance can be improved by using multitimbered or a timber overhang configuration that reduces the effects of localized failure.

The loading profile of wood crib supports is ideally suited to coal mining ground control applications in that a high initial load rate is followed by a large deformation with relatively little increase in loading. Capacities equal to that of reinforced concrete cribbing are easily attainable with multitimbered crib constructions with yield characteristics more compatible to roof and floor convergence.

In general, laboratory test results of wood crib specimens should be viewed as optimum performance. While underground loading of wood cribs follow a similar profile to that observed in the laboratory, load bearing capability can be reduced by boundary conditions that alter the load transfer mechanics of the crib structure.

Preliminary efforts to model overall crib performance from single timber behavior show promise and warrant further investigation. Such models would enable the design of a crib structure with the proper stiffness to be most compatible with a particular mining application.