Basically, a mechanical air separator is constructed with an inner shell and an outer shell. Material fed to a rotating plate is dispersed within the inner shell. Air, pulled in from the outer shell, passes upward through the descending curtain of dispersed feed, elutriating intermediate and fine material out of the feed. The elutriated particulates enter a section containing rotating blades which separate the intermediate material from the fine particulates, returning the intermediate material to the coarse stream. The fine particulates exit from the inner chamber into the outer shell in the air stream, passing through the turbine of the blower which maintains the forced circulation.
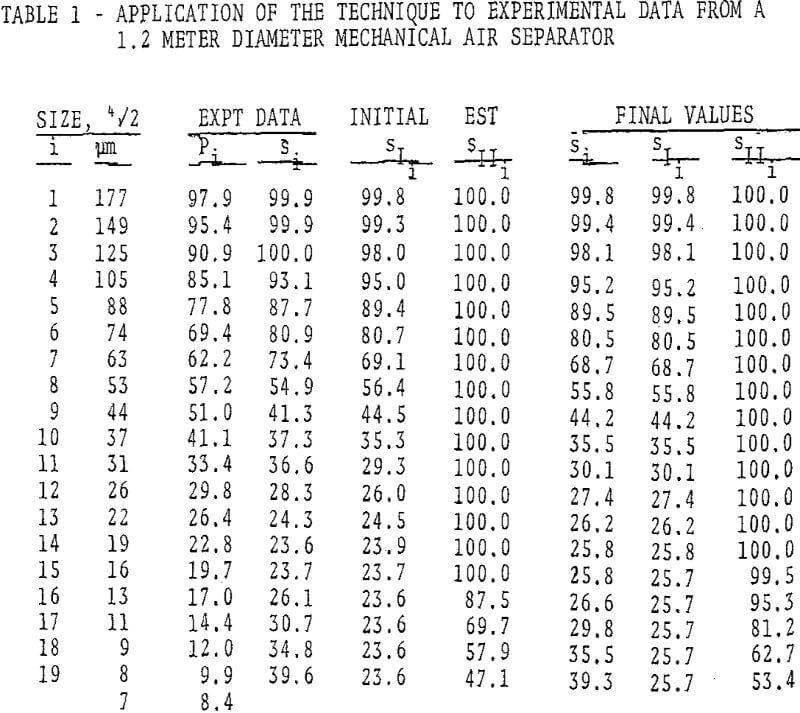
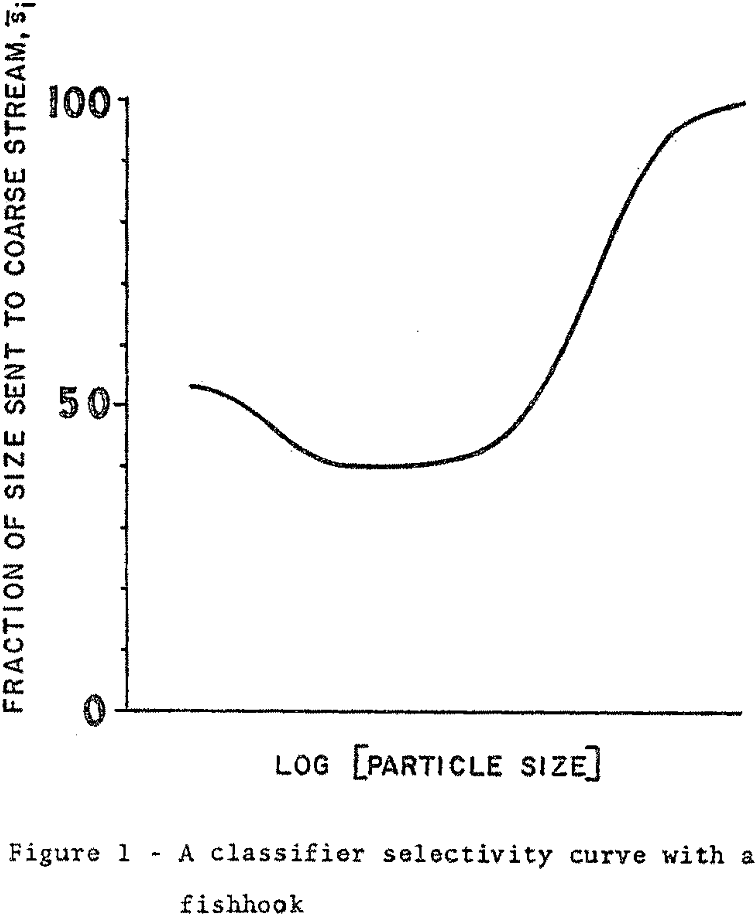
Based upon the proposed mechanism, the selectivity curve for the mechanical air separator was modelled as two classifiers in series. The overall selectivity value, representing the classifier denoted by the dashed line box, is defined as
s (x) = t(x) T/p(x)P
and would be estimated conventionally from the size consist of the feed, coarse and fine streams. It is readily shown that the overall selectivity curve is related to the selectivity values for the primary and secondary classifiers by
s(x) = sI(x)/(l-(l-sI(x)) (l-SII(X)) )
where SI(x) and SII(X), the primary and secondary classifier selectivity values, respectively
When SII(x) = 1, that is, when there is complete separation of the fines from the recycle fluid before it re-enters the primary classification area, then obviously s(x) = sI(x). For the limit of sII(x) tending to zero, all of the fines recycle back into the primary classification area and they must leave in the coarse stream, giving s(x) = 1. In practice, of course, a considerable fraction of all the fine sizes sweeping down the outer shell will pass the fluid re-entry point, so that the apparent by-pass fraction of the second classifier, a2 will never be zero and thus sII(x) will not be zero even for the finest sizes.


We recently published a study of the best garage home air compressors for 2022.
