For some time researchers have attempted to increase drilling efficiency by adding certain agents to the flushing medium. Much of this interest is the result of the observations of Rehbinder, Shreiner, and Zhigach. They postulated that in processes for the mechanical destruction of solids, a region of increased crack formation is created in the deformed layers adjoining that surface of destruction, forming the predestruction zone. The surrounding medium (for example, a liquid), which wets a given solid, will penetrate the embryo microcracks of the predestruction zone. Increasing the molecular affinity of this liquid for the surface of the solid considerably facilitates the deformation and destruction by softening the solid in the zone of increased crack formation. In this manner, the hardness or strength of the deformed body is decreased by the influence of the penetration of the liquid into the predestruction zone. This decrease is known as the Rehbinder effects.
Rehbinder’s work has prompted many other investigators to examine the effect of additives on the mechanical destruction of rocks.
Engelmann, Terichow, and Selim reported that the maximum penetration of the rock by a diamond point in a solution environment was at the isoelectric point of the solution. Robinson, however, reported that his results did not appear to support Rehbinder’s theory.
Joris and McLaren suggested that additives with lower surface tensions than that of water will be more efficient in cooling the diamonds. The effectiveness of such additives in removing the fine cuttings from the face of the bit will also improve the efficiency of the system. Joris and McLaren also reported an improvement in impregnated, bit life and penetration rates with the use of soluble oil additives.
In contrast, Long and Agnew, drilling with surface set bits, reported that lubricating agents increase bit temperature and wear.
A significant change has been reported in the mechanical properties of rock with polar additives with the conclusion that this change in the mechanical properties of the rock in the presence of such additives is due to the hydrophilic properties of the rock.
Ethylene, glycol, glycerine, and anionic detergent were selected for this investigation because of their low surface tension compared with that of water. The surface tension of these additives for the concentrations studied was 42 to 75 percent of that of water. An additive of low surface tension wets the surface of the diamonds more easily than does water and hence could be more effective in cooling the diamonds. Another characteristic of these low surface tension additives is their effectiveness in removing the cuttings and preventing the flocculation of the particles formed in the drilling process.
This Bureau of Mines report combines and expands upon two journal articles written at the Twin Cities Mining Research Center. The objective of the investigation was to study the overall effects of such organic additives on the performance of diamond impregnated bits.
Experimental Design and Instrumentation
Statistical Design of Experiment
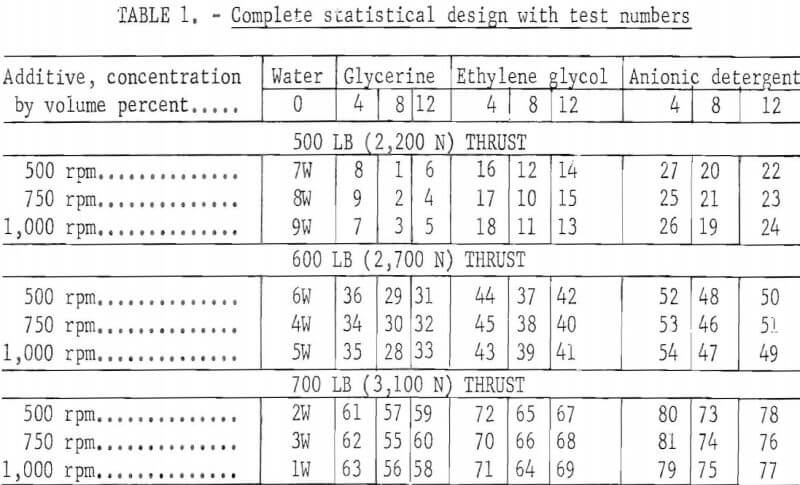
To define the accuracy of the results and to eliminate the unnecessary random and systematic errors that otherwise would occur, this investigation followed a statistical plan based on a 3 by 3 by 3 factorial design. The factors and their levels in the statistical design are as follows:
- Additives: anionic detergent, glycerine, ethylene glycol, and water.
- Solution concentration 4, 8, and 12 percent by volume.
- Thrust: 500, 600, and 700 lb (2,200, 2,670, and 3,110 N).
- Rotational speed; 500, 750, and 1,000 rpm
The complete design with the test numbers is shown in table 1. The test numbers are the order in which the tests were performed, tests 1W to 9W (using water) then test 1 through 81 were completed in that order. Each test number represents one complete test at that specific set of conditions. Three other factors were held constant throughout the test:
- Rock: Sioux Quartzite.
- Bits; Longyear Impregnated industrial diamond bits, 1.25 in (3.18 x 10-³ m) OD, 0.145 in (3.680 x 10-³ m) kerf thickness, all of the same lot,
- Solution flow rate: 0 23 gal/mm (1.451 x 10 -5 m³/sec) at 300 psi (2.1 x 10 6 N/m²).
Three additives and their concentrations were chosen after material testing in chemical environments, and after preliminary drilling tests conducted in our laboratories. The levels of thrust and speed used were based on these preliminary tests and on the torque limitation of the impregnated bits.
Equipment and Instrumentation
The drilling was done with a Cincinnati Brickfond radial arm drill (fig. 1), which served as a selected speed power source and mounting bracket. Since it had sufficient torque for all drilling conditions, it could maintain the constant speeds desired.
The thrust was applied to the bit by a 5-in (1.27 x 10-³ m) diameter air cylinder which was mounted on top of the drill and thus applied constant thrust to the spindle throughout its entire vertical travel. The air was supplied at line pressure, then reduced to the desired pressure at the drill by a regulator and directed to the appropriate section of the air cylinder by a two-way valve. To simplify adjusting the air pressure, the actual thrusts used were 491, 590, and 688 lb (2,184, 2,624, and 3,060 N) which correspond respectively to 25, 30, and 35 psi (1.7, 2.1, and 2.4 x 10 5 N/m²).
The cooling fluid circulation system main components were a 2 gal/min (1.2 x 10 -4 m³/sec Hydro series 5300 piston pump and a Hydro 3390 bypass valve set at 300 psi (2.1 x 10 6 N/m²). These supplied fluid under 300 psi (2.1 x 10 6 N/m²) through 20 ft (6 m) of ½ in (1.3 x 10-² m) hose to a 0.1916 in (4.866 x 10-³ m) orifice at the water swivel. This system provided a flow rate of 0.23 gal/min (1.457 x 10 -5 m³/sec) through the bit for all drilling conditions. This flow rate was chosen on the basis of the author’s experience with previous drilling tests.
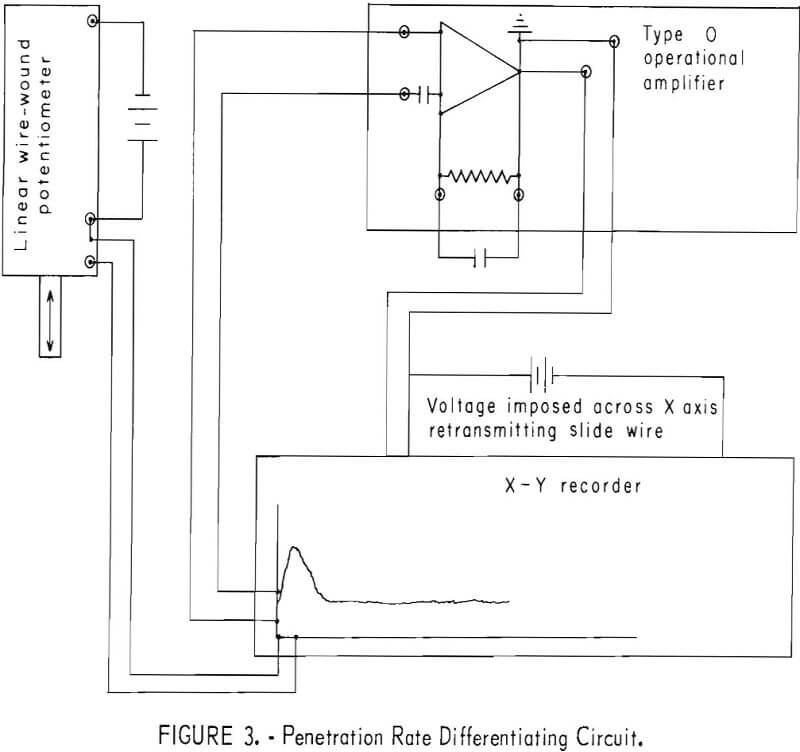
The distance the bit moved vertically (read as penetration in inches) was measured by a linear wire-wound potentiometer mounted on the drill frame and attached to the spindle thrust rod (figs. 1-2). With a voltage applied across the potentiometer, the output voltage, E0, depends on the location of the slide wire on the potentiometer. As the bit moved vertically, Eo changed. Eo was supplied to the X-axis of three X-Y recorders (fig. 2), and thus gave a continuous and positive bit location readout. Once calibrated for Eo and bit displacement, this system proved to be an accurate and trouble-free system. The penetration rate was obtained by imposing a voltage across the retransmitting X-axis slide wire potentiometer of the No. 1 recorder and then transmitting this output voltage to a type 0 plug-in unit that differentiated it continually (fig. 3). This differentiated signal, which is the penetration rate in in./min (m/sec) was then sent to the Y-axis of the No. 1 recorder. This system can be calibrated by running the drill down at a known rate or by putting the X-axis of the No. 1 recorder on sweep. Because this system was particularly sensitive to external electronic noise, all leads were shielded and properly grounded, and a capacitance of approximately 5 mf was connected externally across the resistor of the differentiating circuit.
The thrust applied to the bit was measured by a strain gage load cell located between the air cylinder and the bit. The load in pounds was displayed

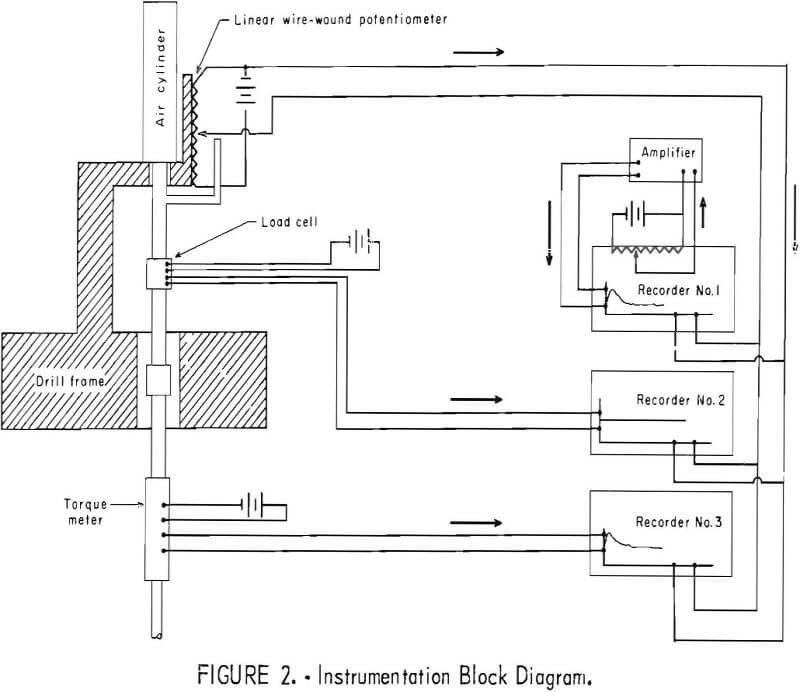
in the Y-axis of the No. 2 recorder. The system was calibrated by placing a commercial load cell under the bit. Electrical balance was obtained with an external potentiometer.
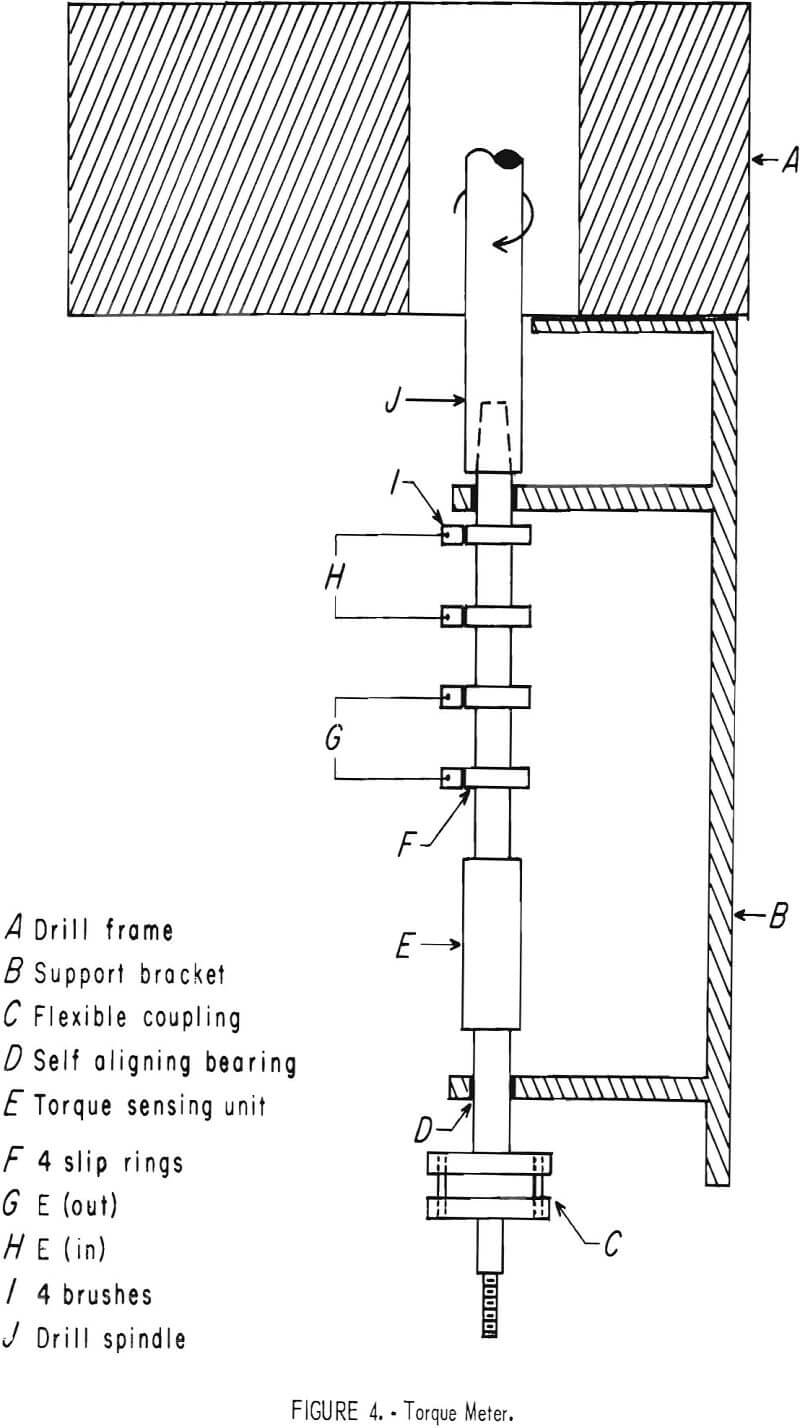
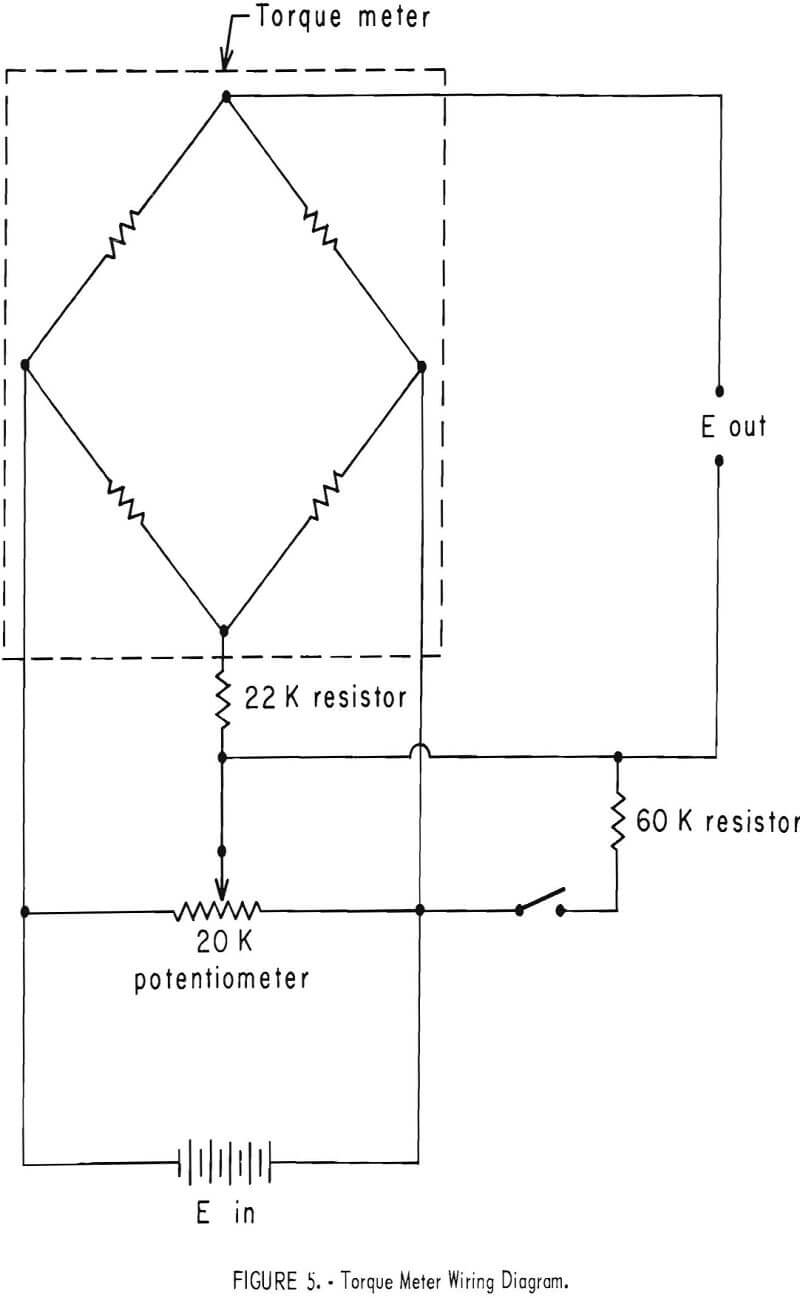
A Baldwin-Lima-Hamilton Type B torque pickup attached between the spindle and the bit by a flexible coupling measured the torque required to rotate the bit (fig. 4). This cage-type strain gage torque meter is insensitive to thrust and bending, and its input and output voltages were transmitted from the torque meter by four silver slip rings and 12 graphite copper brushes. The output voltage (torque) was supplied to the Y-axis of recorder No. 3. The system was calibrated by shunting a 60,000-ohm resistor across two input-output leads and adjusting the input voltage to obtain the correct output. A simplified wiring diagram (fig. 5) shows the location of the 20 k balancing potentiometer. This potentiometer is necessary so that both electrical and mechanical zero can be achieved. The slip rings and brushes were cleaned several times a day, and the zero of the recorder and calibration of the torque meter were checked before each test.
The sliding friction tests were run on a Dow Corning Alpha LFW-1 friction testing machine consisting of a rotating metal ring and a stationary sample block. The sample was loaded normal to the ring and the frictional force was measured by a strain gage load cell (fig. 6). The wear of both the ring and block was measured by a specially constructed linear transducer system, which was mounted on the frame of the machine. This system measured the movement of the sample holder knife edge and thus measured the total wear of both the ring and the block.
The transducer was a Statham model 4C3 with a displacement range of 0.0047 in (1.2 x 10-³ m). The excitation and balance controls were provided by a Statham model UR5 analog readout unit with the output signal recorded on a two-channel oscillograph recorder. When calibrated with a 0.001-in (2.54 x 10 -6m) micrometer, this system for measuring wear was found to be accurate and linear over the complete displacement range.
The rotating rings made of diamond drill matrix material were machined to ±0.0005 in (1.270 x 10 -5 m). The sample blocks were made from single crystals of quartz prepared with critical dimensions to ±0.002 in (5.081 x 10 -5 m). The samples were lubricated by filling the test cap of the machine with various drilling additive solutions. All tests were run at a rotary speed of 180 rpm and a normal load of 15 lb (66.7 N). All tests were run for 2,000 revolutions because preliminary testing showed the coefficient of friction to be constant after the first 600 revolutions.
Analysis of Experimental Data
Penetration Rate
Figure 7 shows the relative penetration rates achieved with water and with glycerine solution as a function of distance drilled. It is quite apparent that at any point in time after drilling has started, a higher penetration rate is observed with the glycerine solution. Paradoxically, however, if one

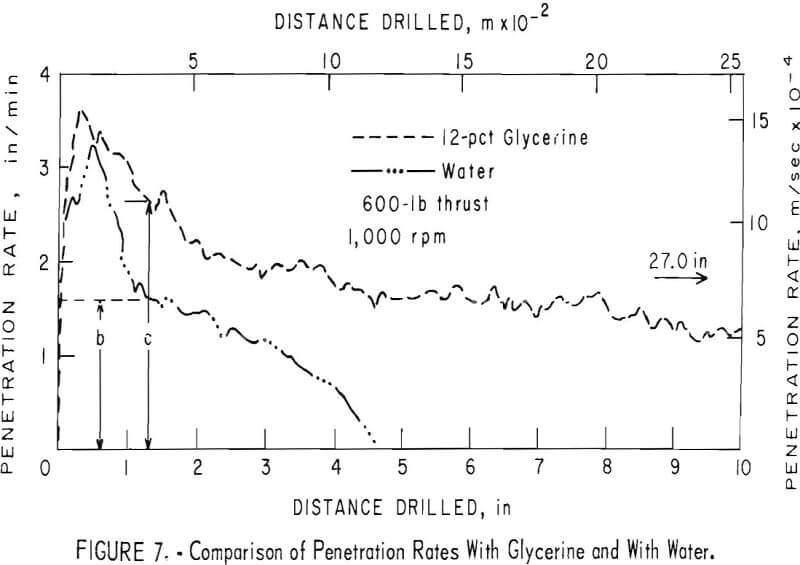
were to calculate the average penetration rate for water, 1.4 in/min (5.9 x 10 -4 m/sec), and glycerine solution, 1.1 in/min (4.7 x 10 -4 m/sec), over the respective life of the bits, there would be a higher average penetration rate for pure water, because of the shorter life of the bit under this condition.
For purposes of illustrating the effect of various parameters on penetration rate, we shall compare the rates at that point where the rate with water has diminished to half its original value. This figure is purely arbitrary and is not used in the economic analysis at the end of the paper.
Energy
In rotary drilling, Teale considered the work performed per minute
W = [pF + 2πNT]…………………………………………………………………………..(1)
where F = thrust,
p = penetration rate,
N = rotational speed,
T = torque.
The energy per unit volume of rock removal is then
e = F/A + 2πNT/Ap in lb/in³………………………………………………………..(2)
where A = area of the annulus.
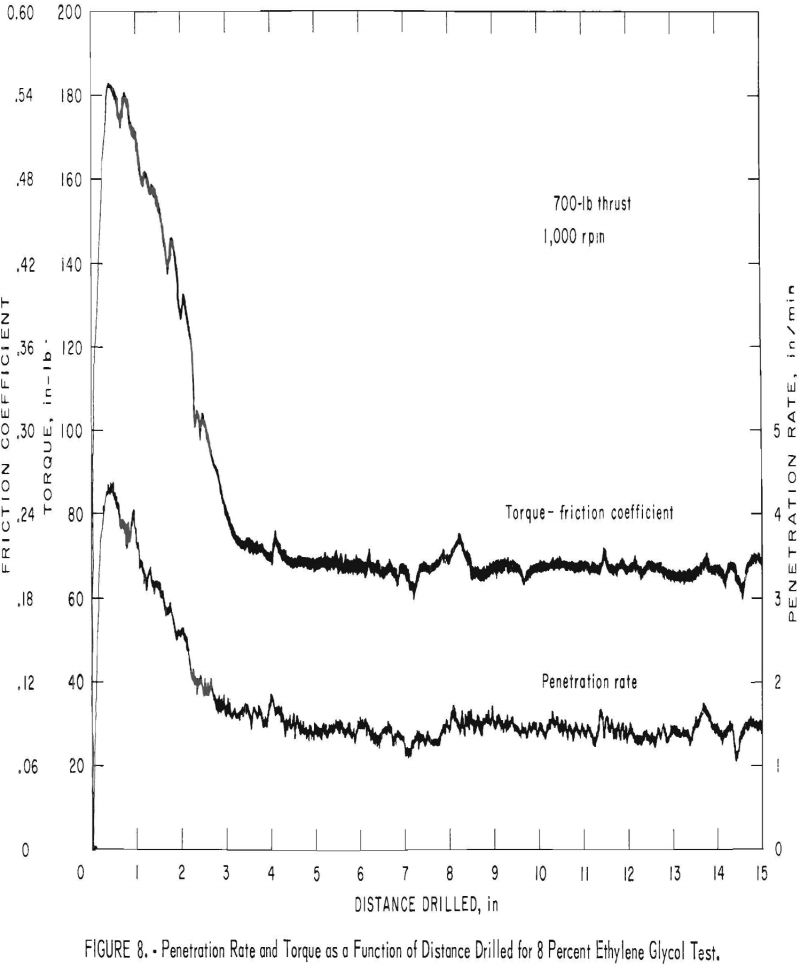
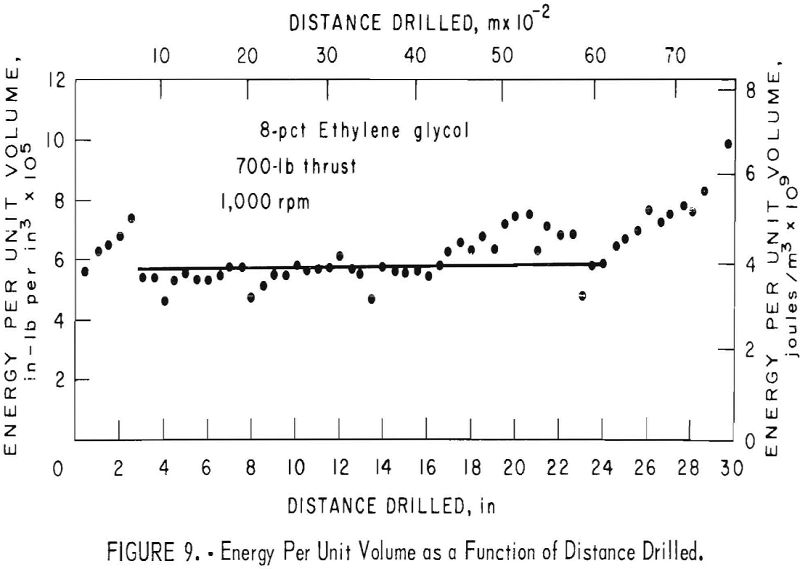
The thrust component was found to be about 1 to 500 in comparison with the rotary component. The energy per unit volume can then be approximately defined in terms of the rotary component only. Teale showed that the energy per unit volume is constant over a wide working range in which the ratio of torque to penetration rate is constant. Figure 8 shows the recorded penetration rate and torque as a function of the distance drilled for the 8 percent ethylene glycol test. Note that the fluctuations in the penetration rate are associated with similar fluctuations in the torque. The energy per unit volume calculated from these data approximates a constant value over the working range (fig. 9).
Friction
Friction at the rock-bit interface in diamond drilling may be defined as the resistance of the rock to the applied tangential force and may be divided into two components: Resistance to sliding and resistance to plowing. The resistance to sliding may be due to adhesion of the asperities at the diamond rock interface as suggested by Bowden in his sliding studies on glass. This adhesive characteristic may be destroyed by fracture at the contact area. Plowing of the rock occurs if the shear stress induced by the diamond overcomes the shear strength of the rock. During the plowing action of the diamond, chips from the rock are pushed ahead or to the sides of the diamond. Appl suggested that the principal mode of failure in this case would be by shearing and might be brittle or plastic.
The coefficient of friction in drilling can then be defined as the ratio of the tangential force to the normal force or thrust.
![]()
where r = effective radius of the annulus, in (m),
µF = coefficient of friction,
FH = tangential force at the rock-bit interface, lb (N),
FV = thrust of the bit, lb (N),
and T = torque, in. lb (N X m).
Since the thrust was kept constant in each test, the coefficient of friction was a function of the torque only.
In the sliding friction tests on the Alpha friction testing machine, the coefficient of friction was obtained by dividing the average frictional force by the normal load.
Wear
A bit usually shows wear in the presence of friction. The wear of the bit can be divided into two main components, (1) wear of the matrix due to the presence of abrasive particles of rock cuttings at the rock-bit interface, and (2) wear of the diamonds due to oxidation or graphitization at high temperatures generated at the rock-diamond interface. The wear of the diamonds and of the matrix affects both the performance and the life of the bit.
Bit life can be described by the statistical theory of reliability. In the simplest case, the reliability of the bit can be defined by

where R (x) = reliability of the bit at total distance drilled x,
λ = constant failure rate of a wear coefficient,
and x = total distance drilled.
From equation 4, it can be seen that if x1 < x2, then R (x1) > R(x2). Since the penetration rate is also inversely proportional to the total distance drilled, we infer that the penetration rate is proportional to the reliability of the bit.
From the above discussion, we define the penetration rate in terms of the reliability of the bit, assuming a linear relation of the form
dx/dt = Po R (x)………………………………………………..(5)
where Po = constant.
For a new bit, the reliability is 100 percent, and hence Po can be defined as the initial penetration rate. In the more general form, we can define the reliability of any device in terms of the Weibull distribution.
![]()
where λ = failure rate,
β = shape parameter,
and γ = location parameter.
Therefore, equation 5 becomes
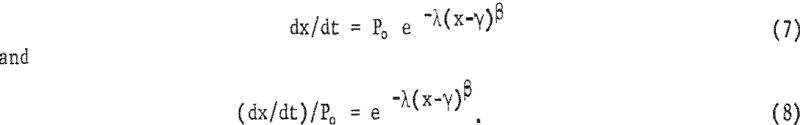
When dealing with failure rates, the Weibull shape parameter, β, is of special importance because it describes the mode of failure. Thus, for β = 1, the failure rate is constant over time as it is for the exponential distribution. A value for β < 1 indicates that the failure rate is a decreasing function of time, and a value β > 1 means that the failure rate increases with time.
Equation 8 expresses the penetration rate as a percentage of the initial penetration rate. A method of estimating β is shown and the failure rate of the bit, can be obtained directly. This failure rate, β is considered as an index for comparing the effect of the solutions under investigation and also as a wear coefficient for the bit.
From equation 2, we can approximate the penetration rate
dx/dt = 2πNT /A. e………………………………………………………..(9)
Assuming that the energy per unit volume is approximately constant over the working range as shown by figure 9, and that the coefficient of friction is proportional to the torque as shown above, equation 9 can be expressed in terms of friction as
dx/dt = c·µ………………………………………………..(10)
where c = constant,
and µ = coefficient of friction.
By substituting this relation, we can express equation 7 in terms of friction as
![]()
where µo = the initial coefficient of friction.
Equation 11 expresses a relation between the wear coefficient and the coefficient of friction at the rock-bit interface.
The wear measured in the sliding friction tests on the Alpha friction machine was the change in the distance between the center of rotation of the ring and the knife edge on the sample block holder, read to the nearest 0.0001 in (2.54000 x 10 -6 m). This change in distance was taken to represent the total wear of the ring and the block.
Discussion of Results
Penetration Rate
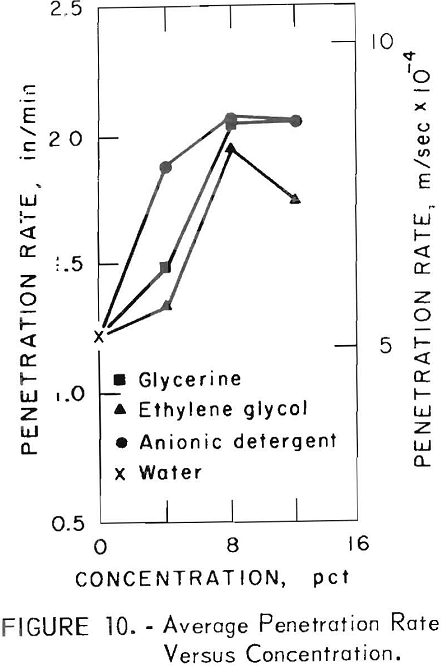
One effect of additives in drilling rock with impregnated diamond bits is to increase the penetration rate. Figure 10 shows the average penetration rates with the various solutions as a function of their concentrations. The penetration rates shown at each concentration are the rates as defined previously. All solutions were significantly better than water (0 percent additive concentration). The penetration rates for all additives approached a maximum at a concentration of 8 percent and decreased at high solution concentrations. The anionic detergent caused a significant increase in penetration rate at a concentration of only 4 percent.
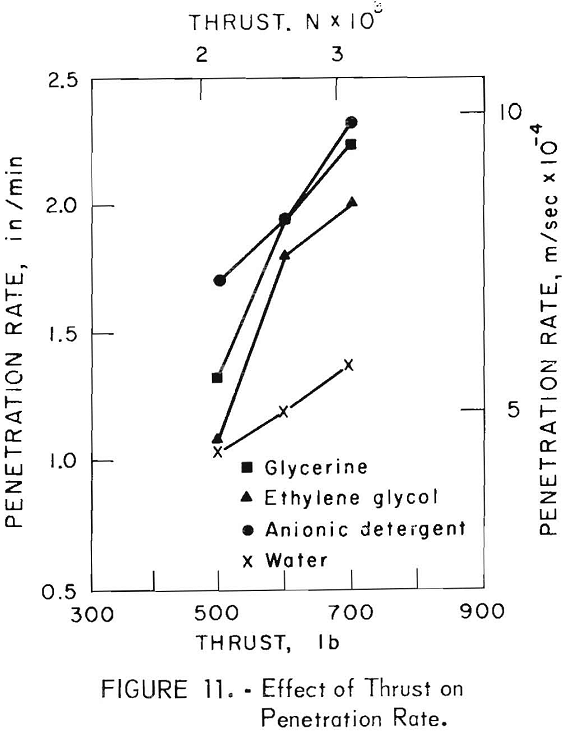
The effect of thrust on penetration rate is shown in figure 11. As expected, the highest penetration rate was attained by all four circulating media at the highest thrust.
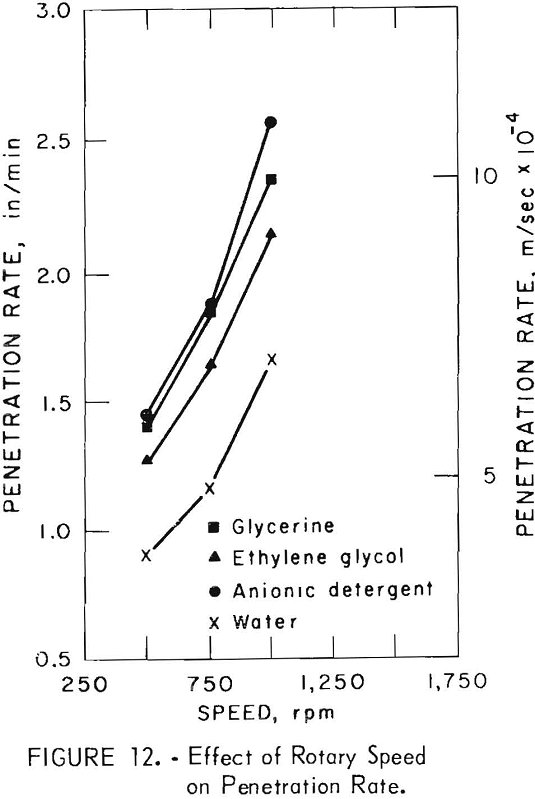
Figure 12 shows the effect of rotary speed on the penetration rate. For all circulating media the maximum rate was attained at the highest rotary speed, 1,000 rpm.
Energy Consumption
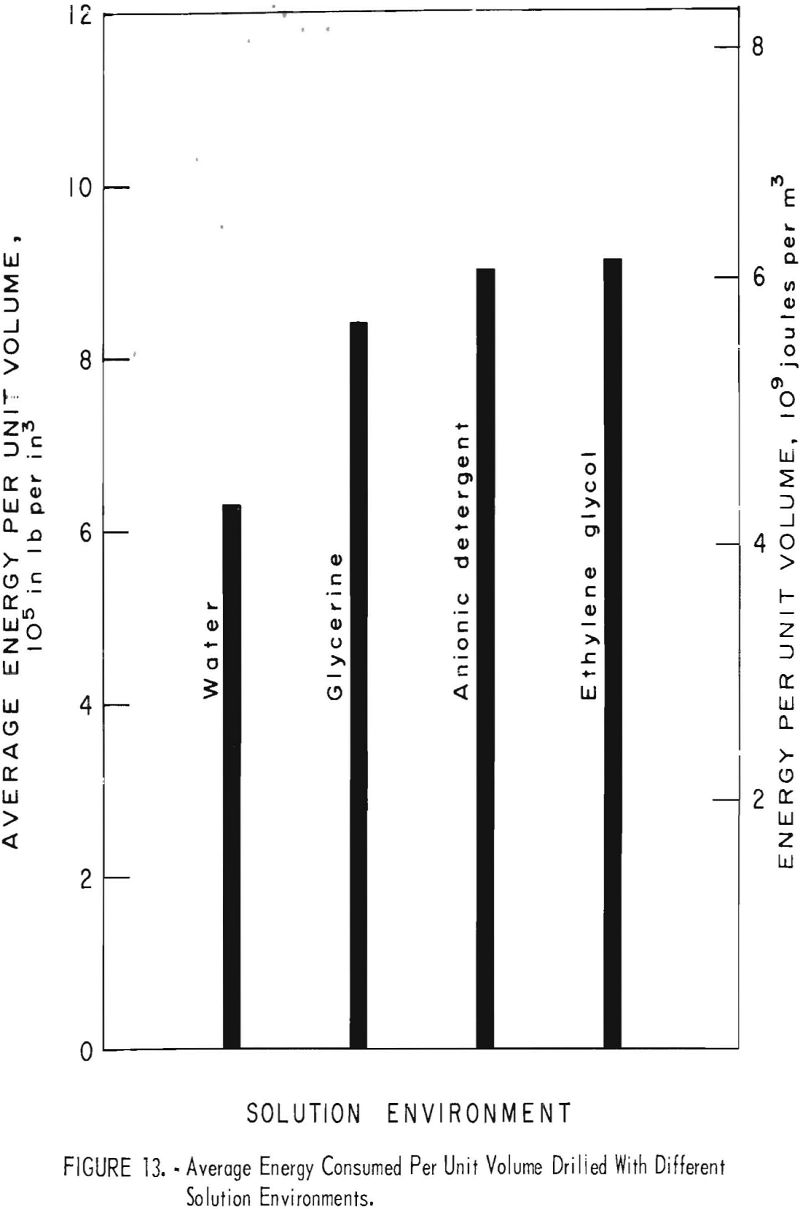
Energy consumed per unit volume drilled with the various additives as shown in figure 13 is significantly higher than when drilling with only water. This result is contrary to what Joris and McLaren reported. A close examination of the energy consumption in figure 14 shows that the glycerine and ethylene glycol solutions have a minimal energy per unit volume consumption at 8-percent concentration,, but that the detergent does not exhibit this trend. This difference could indicate that the optimum detergent concentration was not tested in this investigation.
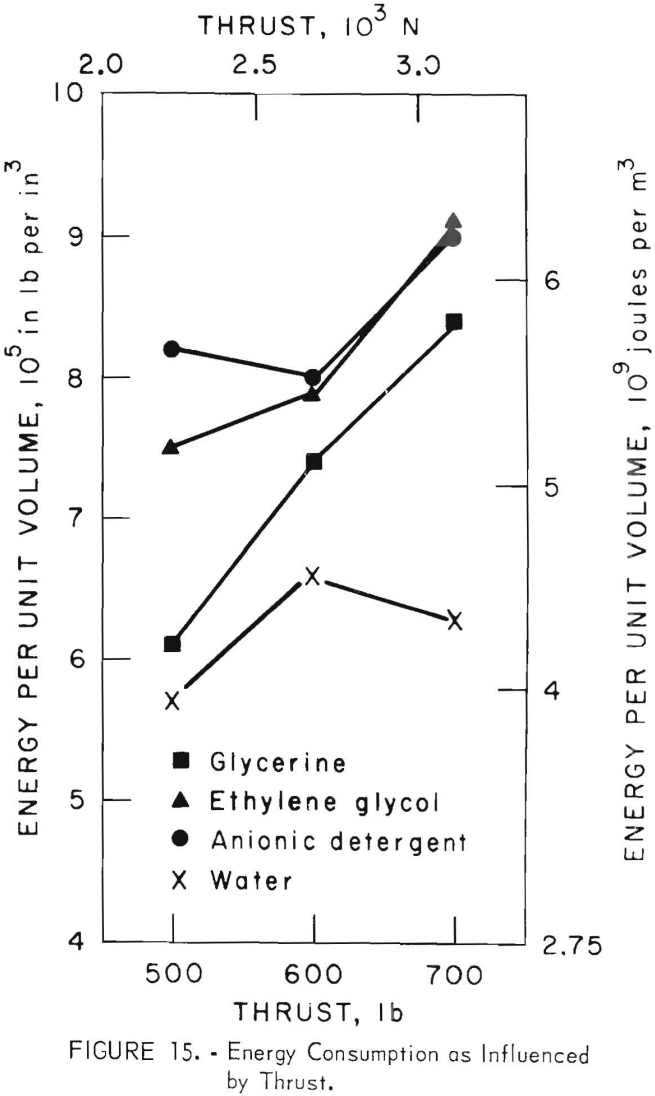
The energy per unit volume consumption is greatest with the additives at maximum thrust (fig. 15). This observation may be explained by the fact that this is the condition of maximum penetration rate, and therefore the energy transfer is not as beneficial.
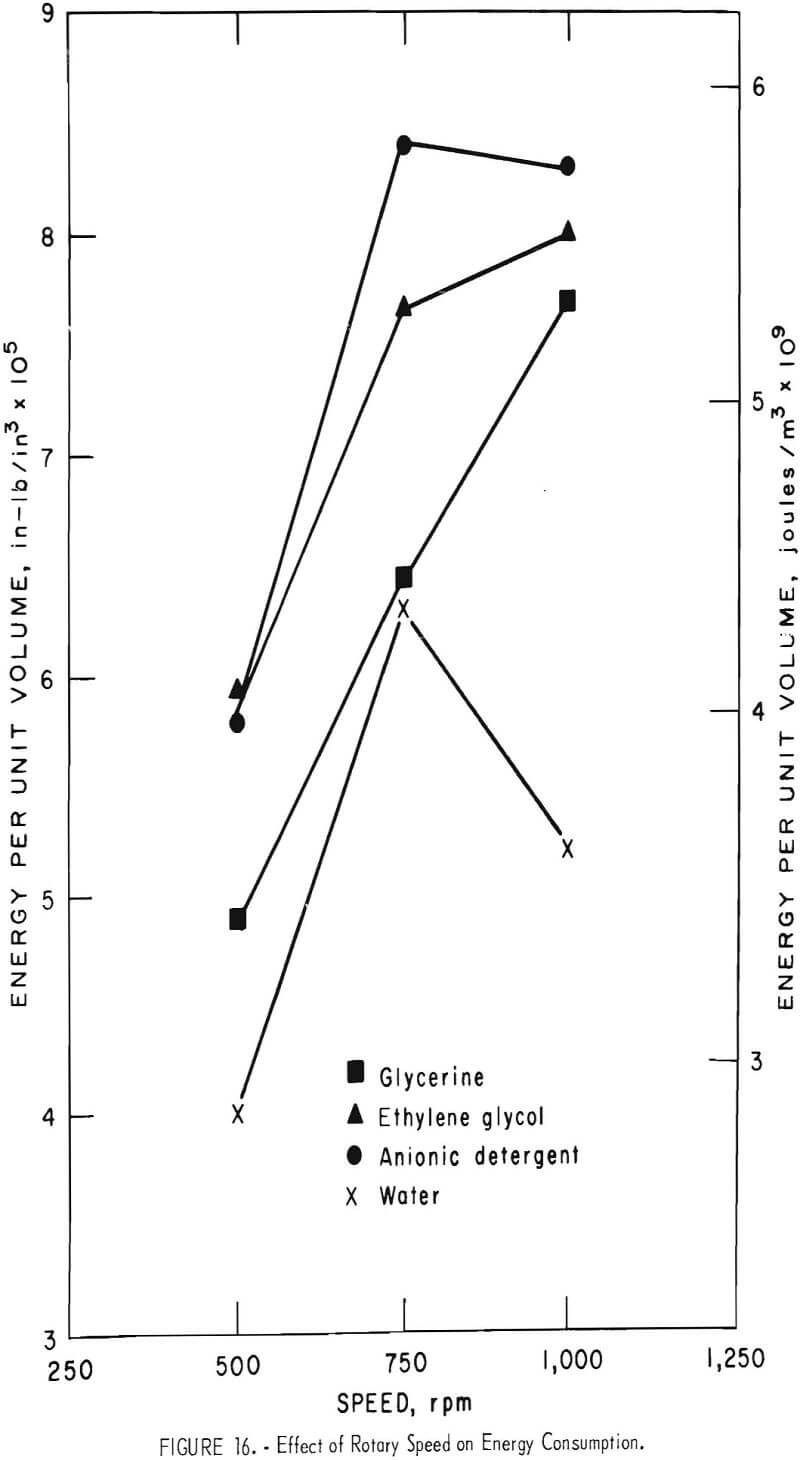
Figure 16 contradicts this hypothesis in that the maximum energy consumption for detergent and for the water is at 750 rpm, a value which is not associated with the maximum penetration rate.
Coefficient of Friction
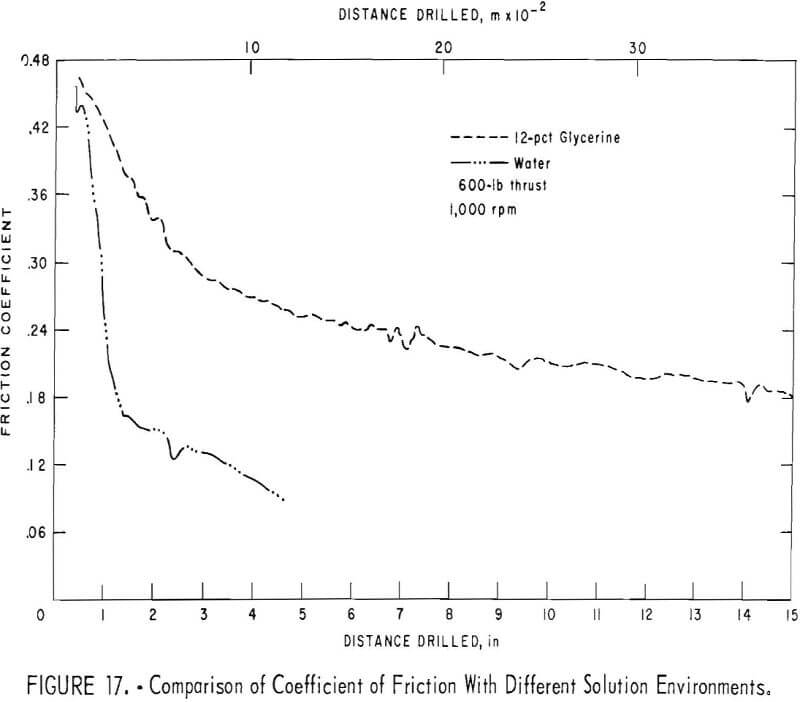
The coefficient of friction in the presence of the organic additives was usually higher than in the presence of water only. In a typical case with 12 percent glycerine (fig. 17), the coefficient of friction was higher than that with water and the two approach a common value at ½ in (1.3 x 10-² m) distance drilled. This relation is analagous to the observation made of their

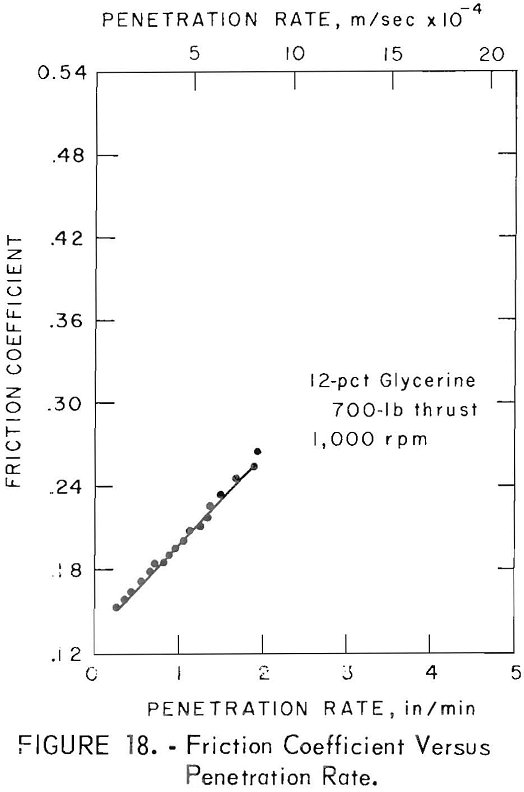
penetration rate curves (fig. 7). The relation shown between the coefficient of friction and penetration rate proposed in equation 10 (fig. 18) was linear over the working range when the energy per unit volume consumed was constant and the thrust was held to the prespecified value. This relation was observed for all the tests with a correlation coefficient of 85 to 95 percent upon fitting the data by the method of least squares. From equation 9, the slope of this line is then a function of the energy per unit volume consumed. When the volume drilled approaches zero, the coefficient of friction shows a finite value. This would imply that the finite amount of friction at zero penetration would represent the sliding friction, since no plowing effect exists.
Laboratory tests on an Alpha friction testing machine using quartz against a rotating metal ring, composed of diamond drill matrix material, were performed with the same solutions and solution concentrations as were used in the drilling. All three solutions reduced the friction as compared with water, and the friction decreased as the concentration of the additives increased (fig 19).
The coefficient of friction measured on the Alpha machine is the sliding friction between the metal of the drill bit and the rock, whereas the friction
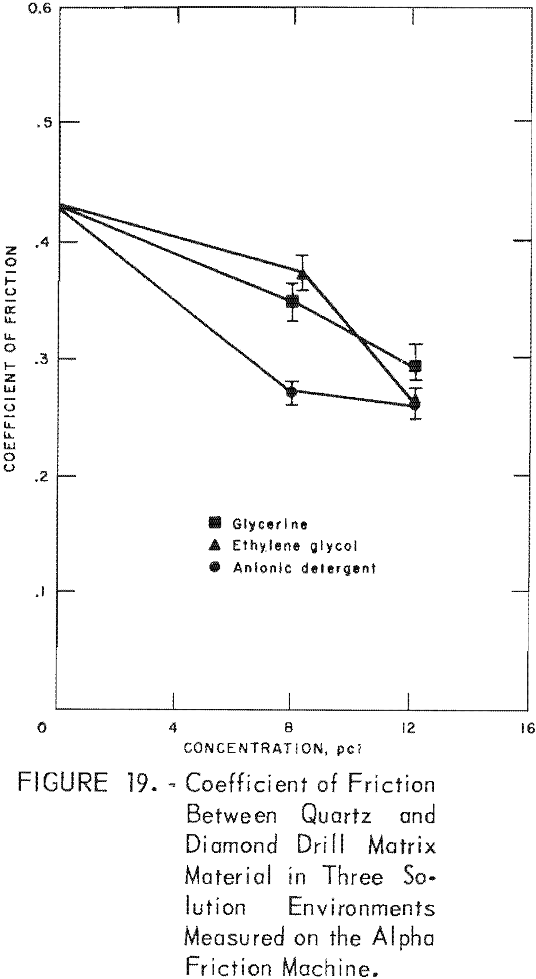
measured in the drilling tests is mainly the result of the plowing action of the diamonds in the rock. The results of the two friction tests indicate that the additives tend to increase the plowing.
Wear Coefficient
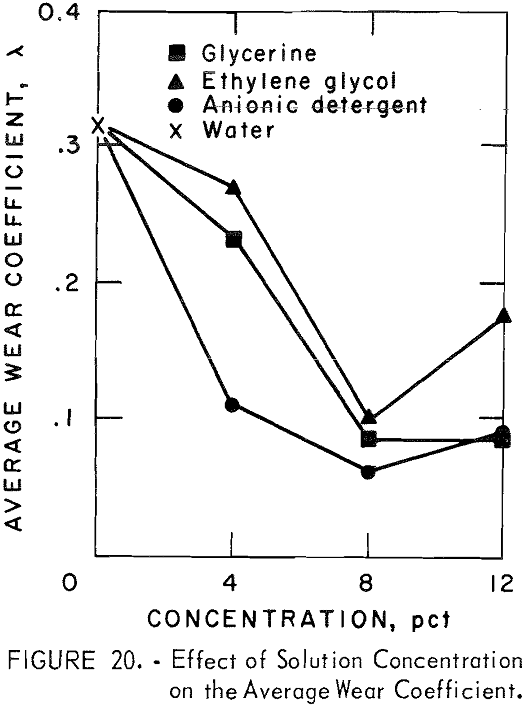
With λ, the wear coefficient, as a measure of the effectiveness of our organic additives, we observe that all additives decreased the wear coefficient relative to that observed with water. Figure 20 shows the effect of the solution concentrations on the average wear coefficient of the bit. Note that the minimum wear coefficient for all solutions was at 8 percent concentration: the 8 percent anionic detergent gives the lowest value.
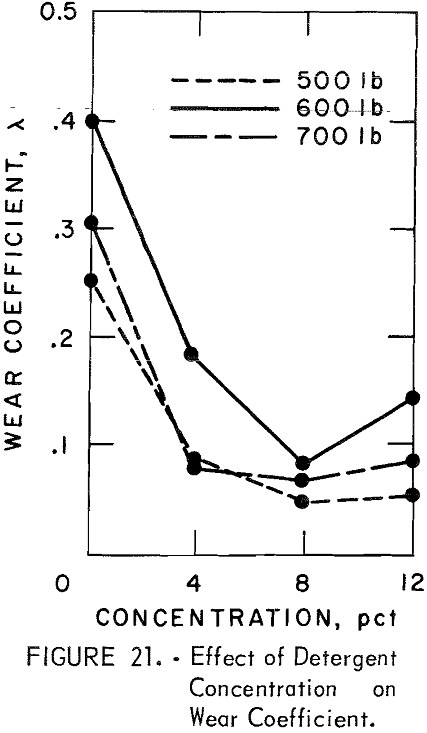
Figure 21 shows the wear coefficient as a function of anionic detergent concentration at three levels of thrust. The lowest wear coefficient is 0.042 with 8 percent anionic detergent, or 89 percent less than with water (zero concentration).
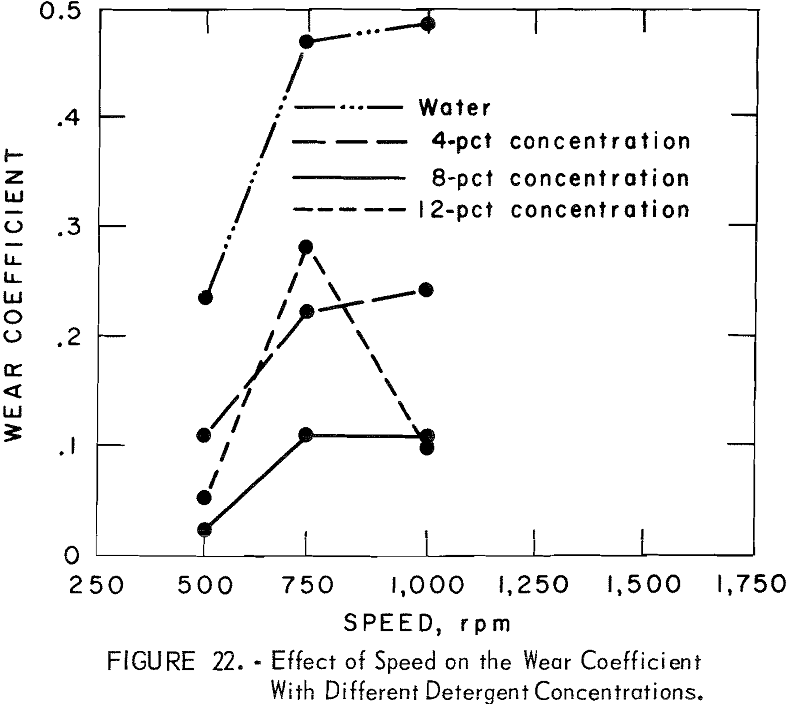
Figure 22 shows the effect of speed on the wear coefficient. As shown, the best condition observed is at low speed and 8 percent detergent. The wear coefficient at this condition is 10 percent of that attained with water under the same mechanical conditions.
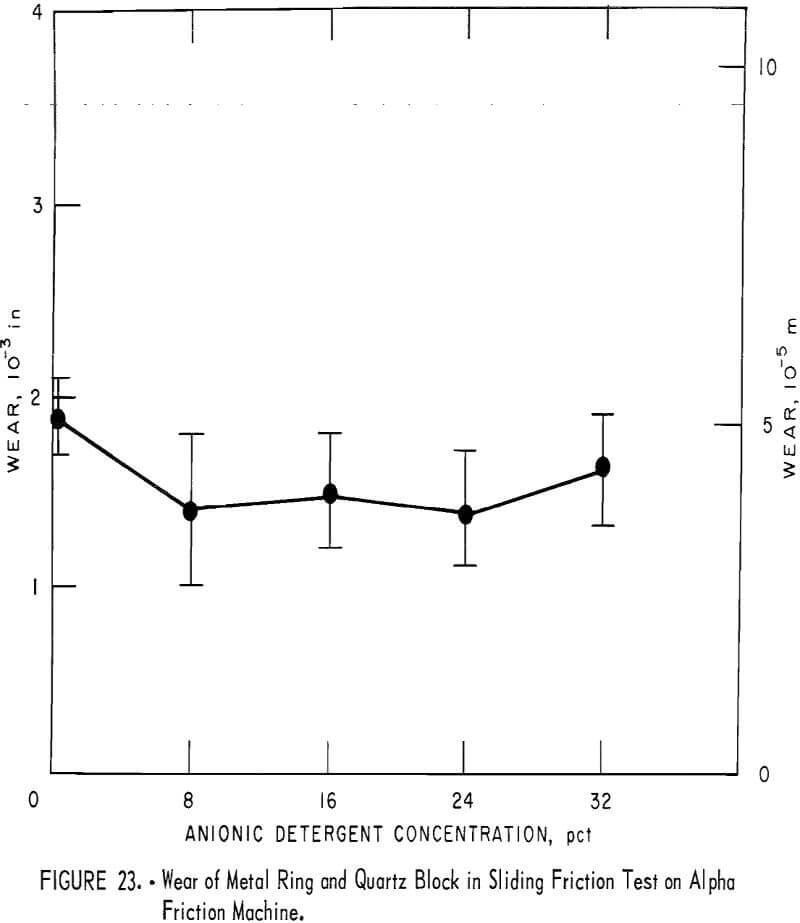
The sliding friction tests with the Alpha friction machine indicated a similar wear as related to detergent concentration as did the drilling tests in figure 21. The wear was less than when water was used, but remained fairly constant as the concentration was increased beyond 8 percent up to an extended range of 32 percent concentration (fig. 23).
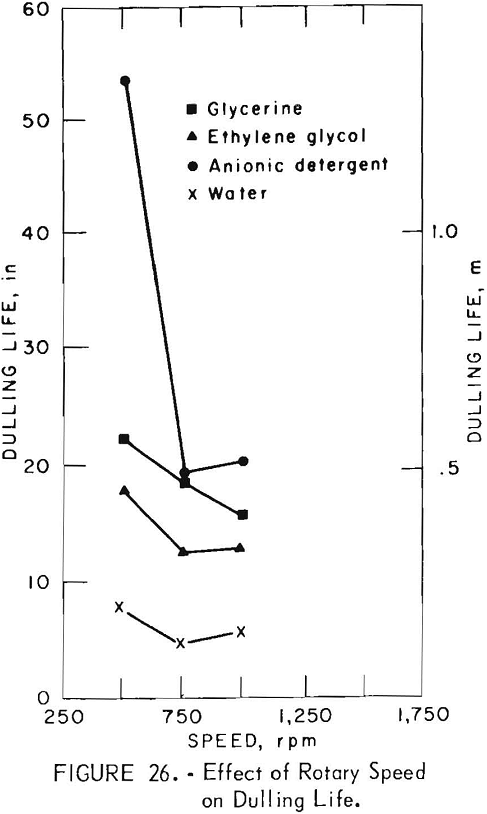
Dulling Life
In each test, drilling was continued until the penetration rate dropped to 0.25 in/min (1.05 x 10 -4 m/sec), at which point the bit was considered to be dull and the test ended. This distance drilled was recorded as the dulling life of that particular bit under those specific operating conditions. The dulling life is important because the total bit life is directly related to it.
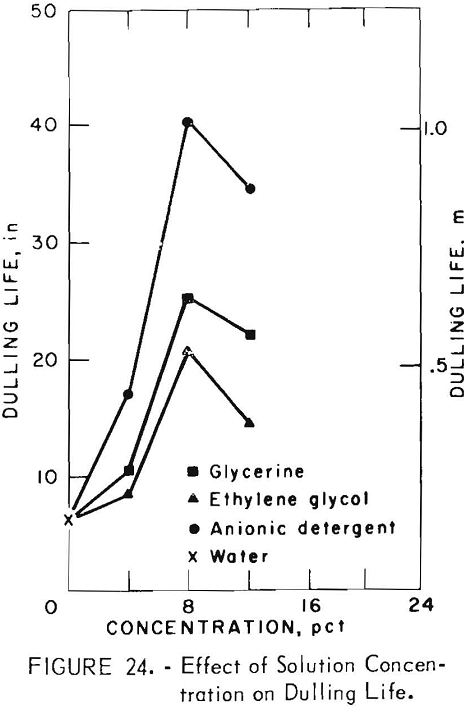
Figure 24 shows the effect of the solution concentration on the dulling life of the bits averaged over all other test conditions. All three solutions exhibited the greatest influence on dulling life at the 8-percent-concentration level; at all concentrations, all additives performed better than water.
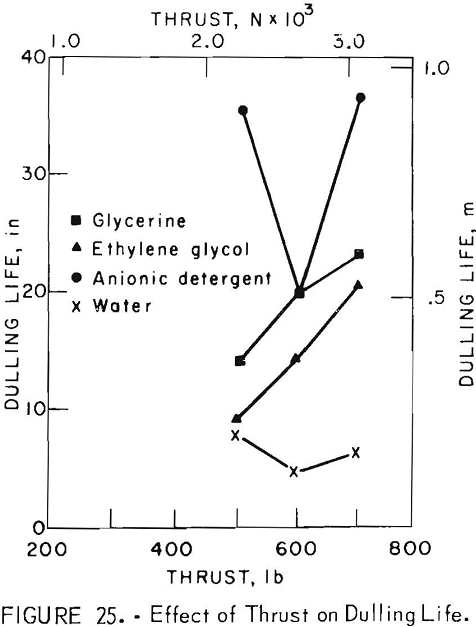
Contrary to what would be expected, the highest level of thrust shows the longest dulling life for the solutions (fig. 25). The low value attained with detergent at 600 lb (2,700 N) thrust probably indicates an interaction of the operating parameters, but is definitely a valid point since each point on the curve represents the average of nine tests for each solution and three each for water. The nine tests for this point are tests 52, 53, 54, 48, 46, 47, 50, 51, and 49. The other points on this graph and also the points on other graphs are the averages of the tests in that block of tests that are described by that graph.
For all circulating media, the longest dulling life is attained at low rotary speed (fig. 26).
From the results it appears that the two most favorable conditions, depending on the response desired, are as follows:
- For optimum penetration rate 700 lb (3,100 N) thrust, 1,000 rpm, and 8 percent detergent.
- For longer dulling life 700 lb (3,100 N) thrust, 500 rpm, and 8 percent detergent.
Diamond Impregnated Bit Total Life
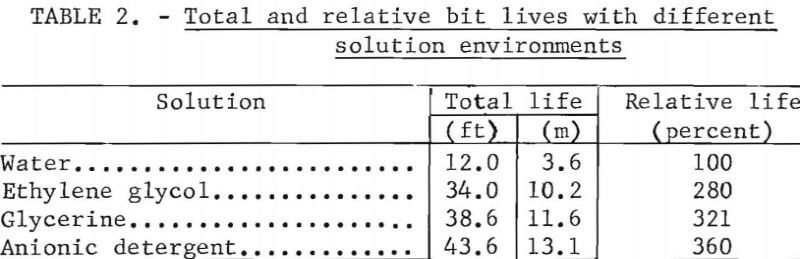
Bit life is of special interest because it is relative to the cost of any drilling operation. A final group of four tests at 700 lb (3,100 N) thrust, 500 rpm, and 8 percent solution was performed to test the effect of the solution on the total life of the bits.
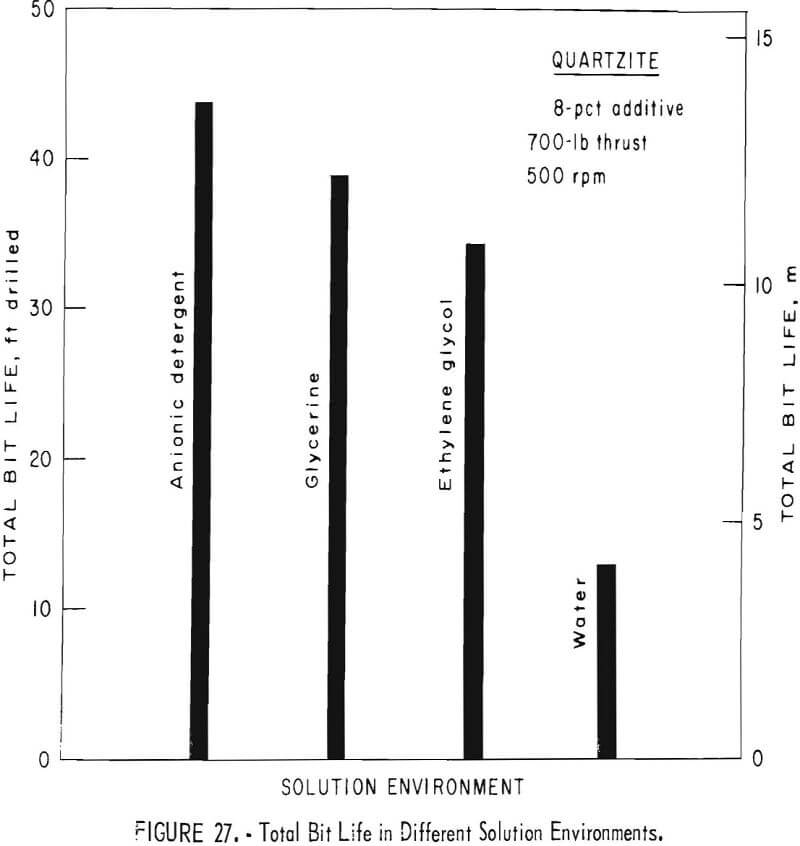
The total life measured in these tests is defined as the distance drilled, until complete wear or destruction of the diamonds occurs, and no bit reconditioning is possible. The bits were reconditioned by sandblasting when the penetration rates dropped to 0.25 in/min (1.52 x 10-² m/sec). Figure 27 compares the total life of impregnated diamond bits attained with each 8-percent-solution environment. For the three solutions, improvement in total life is as follows:
Another parameter of improvement observed was the number of times the bits needed resharpening to attain their total life. Under the defined test
conditions, all solutions decreased the number of sharpenings required as compared with water. This is as it should be, since all solution levels were found to increase the dulling life. It should be noted that the first dulling life of the bits is the longest.
Diamond Surface Set Bit Total Life
Because of the observation made by Long and Agnew, Longyear 1-in (2.5 x 10-² m) ID surface set bits were used to compare the bit performance with water and with 8 percent anionic detergent at 700 lb (3,100 N) thrust and 500m rpm. The penetration rate and the friction coefficient were observed to be higher in the presence of the additive, like the observations for the diamond impregnated bits. The total bit life of 21 ft (6.3 m) obtained in the presence of the detergent was significantly better than the 11 ft (3.3 m) obtained in the presence of water, but not so large as the improvement attained with the diamond impregnated bits.
Statistical Analysis
The results presented so far for the impregnated bits have been based on a statistical experimental design. The analysis of variance of the results shows that all solutions and solution concentrations used in the tests significantly improved the penetration rate, the wear coefficient, and the total life of the bit, the confidence coefficients being 90 to 95 percent.
The sliding friction and wear tests on the Alpha friction machine were performed under another experimental design with five replications of each test. The standard deviation for each set of tests is shown on all the friction and wear graphs.
Cost Analysis
The data have demonstrated that all solutions significantly increase the total bit life, and therefore can reduce drilling costs.
To determine the savings that additives offer, the cost of drilling a hypothetical 1,000 ft (300 m) hole in quartzite was calculated on the basis of table 3. The number of bits and the amount of additive needed were based on the information obtained from the impregnated bit total life tests. The time needed to complete the hole was a function of the penetration rates attained in the total life tests and the number of times the bits had to be replaced. Power was a function of drilling torque and total drilling time.
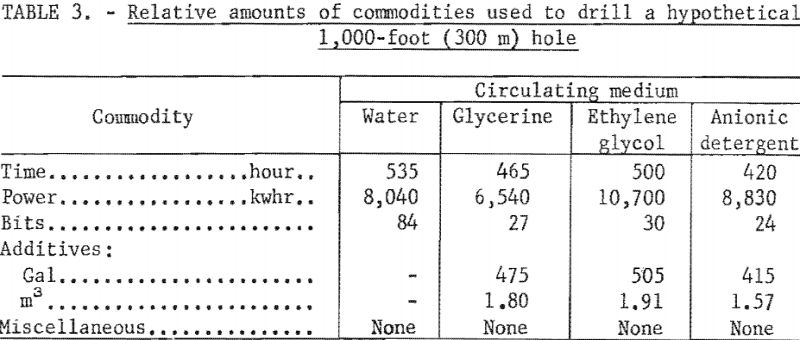
To achieve a better comparison these data in table 3 were converted to dollars (table 4) by these conversion factors:
Labor (driller and helper) $10.00 per hour
Power $0.04 per kwhr
Bits $50.00 each
Additives:
Glycerine $2.50 per gallon ($660 per m³)
Ethylene glycol $1.40 per gallon ($370 per m³)
Anionic detergent $2.00 per gallon ($530 per m³)
Miscellaneous $1,000.00 per 1,000 ft (300 m) hole
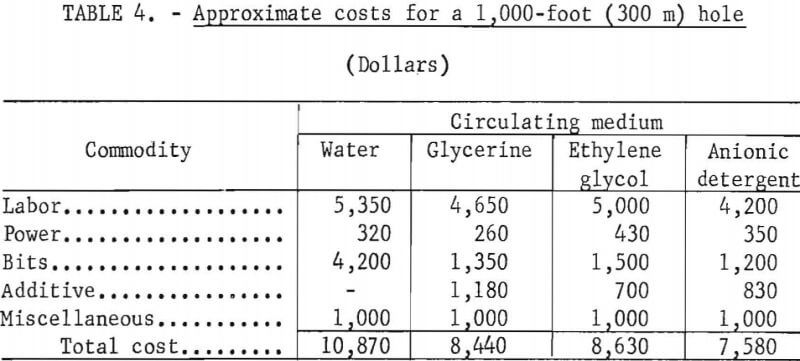
From the table it is seen that the additives gave a substantial saving over drilling with water, chiefly because of lower bit costs. Since costs vary with location, each operator should calculate the cost for his particular local conditions according to table 3.
Conclusions
The most interesting features of the observations we have made are the apparent paradoxes they contain. First we observe that the coefficient of friction in drilling increases in the presence of organic additives that normally decrease sliding friction. Perhaps indicating a more efficient transfer of energy from drill to rock and, therefore, greater penetration rate. However, since the action of a diamond bit is more nearly plowing than sliding, we will attempt to explain this incongruity by considering a related variable. It has been shown that the energy consumed per unit volume drilled is directly related to the observed coefficient of friction at constant penetration rate. Therefore, the energy per unit volume is also higher in the presence of the additives. We are now faced with the question of which is cause and which is effect, friction or energy. Is the energy higher because the coefficient of friction increased or is the friction higher because the energy per unit volume increased? If the latter relation is true, and if we consider the energy per unit volume as an index of rock strength, then we have observed a “negative Rehbinder effect.”
Another observation that appears to be contrary to reason is the lower wear coefficient, λ, in the presence of all additives. Normally we associate wear with high friction. In this investigation, however, we observed that additives simultaneously increased drilling friction and yet decreased wear.
To resolve these apparent contradictions, we have arrived at the following conclusions:
- The organic additives effectively increased the penetration rate and the life of the diamond bits in Sioux Quartzite.
- Anionic detergent, in an 8 percent by volume aqueous solution, was the most effective additive in both respects.
- These observations give no inherent proof that the improvements noted can be attributed to the solutions’ having reduced the strength of the rock (Rehbinder effect). This conclusion does not, however, deny the Rehbinder effect, which has been well stated in the literature.
- We believe that this investigation supports the hypothesis of Joris and McLaren that the wear of diamond bits is due to oxidation and/or graphitization of the diamonds. If this hypothesis is correct, drilling with water as a coolant generates sufficient heat to permit the metastable diamond to either oxidize or undergo the transformation to graphite. A wetting agent added to the water may increase the rate of heat transfer at the diamond solution interface and thereby lower the temperature of the diamonds and their rate of transformation to graphite. As solution concentration increases, however, the increasing viscosity will tend to increase the thickness of the laminar boundary around the diamonds and thereby decrease the rate of heat transfer. Thus, one may expect a minimum point in the curve of diamond wear coefficient as a function of solution concentration. This minimum point was indeed observed with all solutions tested in this investigation.
- Whatsoever the local price structure may be, one may confidentially assume that hard rock drilling with water will not be as economical as drilling with an anionic detergent solution.
