Table of Contents
Hydraulic properties and characteristics of copper ore associated with the Casa Grande deposit at the Casa Grande mine are investigated by the Bureau of Mines to assess permeability and its impact on flow capacity during in-place, copper leaching operation. The copper ore is a heterogeneous, unsaturated, and fractured medium in which the permeability is dominated by a network of macrofractures, defining blocks of rock of various sizes. Upon saturating the macrofractures, these act as a network of distributed sources and sinks for flow of solution into and out of the rock matrix. Since copper is disseminated throughout the rock matrix, understanding and exploiting permeability conditions is essential for successful leaching operations in both the matrix and fracture system. This study provides insight into fluid flow behavior within the rock blocks, following saturation of macrofractures.
In general, it is difficult to quantify unsaturated flow in a heterogeneous rock mass. Moreover, few direct measurements of permeability and flow characteristics have been made. One problem hindering direct measurement is associated with the excessive time involved (months or years). Another stems from limitations in test equipment.
The approach used to assess transient migration of fluids at the Casa Grande mine site first estimated hydraulic properties indirectly, using models that account for dependence of saturation on water pressure head (also known as matric potential, capillary pressure, and suction head). Empirical relationships associated with retention properties of the porous medium are then combined with theoretical models of unsaturated flow to approximate permeability and hydraulic conductivity relationships. In turn, this information and appropriate boundary conditions are combined for input into a two-dimensional, unsaturated, finite element flow code called TWOD (Nieber et al, 1991). Results are used for the development and optimization of a site specific hydrologic design for in situ leaching in heterogeneous, fractured, and initially unsaturated copper oxide ore deposits.
Physical Property Assessment Copper Oxide Ore
Sample and Petrographic Description
Representative samples of copper ore were obtained from drillholes at the 335 m level (mean sea level) of the Cyprus Casa Grande mine. These samples were used to assess the spatial variability in hydraulic properties between these boreholes. Six 2.54-cm diameter by 2.54- cm length samples were prepared from each drill cores and tested for saturated hydraulic permeability and porosity by the mercury porosimetry method.
Thin sections were prepared for determining the predominant mineralogy, texture and porosity of the copper ore. Examination of these sections were aided by using a standard axioplan microscope at 3x magnification with a fullwave gypsum filter. The typical mineral assemblage consisted of fine grained rounded quartz mass, with phenocrysts of altered plagioclase feldspar (now kaolinte), biotite, hematite and quartz.
By using an x-ray, electron microprobe, elemental distribution maps were prepared. These maps demonstrate that aluminum was present among the primary elements associated with plagioclase feldspars. This suggested the presence of kaolinitic clay. Copper was found to be associated with both the altered plagioclase feldspar and biotite minerals. The mineralization suggests that preexisting microfractures once served as preferential pathways for the primary deposition of copper and quartz. These ancient microfractures now appear as solid red stringers, or meanders, throughout the sample. The Quartz, however, showed no association with either the mica or clay minerals.
Discontinuities are evident in all of the copper ore samples, as a result of two distinct porosity systems. Examination of back scattered x-ray images at various magnifications, reveals a bimodal porosity distribution. A magnification of 40 x reveals microfractures, while a magnification of 3000 x reveals the existence of micropores at grain boundaries. The present microfractures are believed to represent a distinct episode of failure since they transect fractures previously filled with copper and quartz. It is important to note that these microfractures provide a network for the lixiviant to access copper hosted minerals, increasing the relative surface area for contact. The microfactures appear to have, similar aperture range (5-15 micron) in both the feldspars and biotite minerals, while smaller apertures exist in those cracks transecting the quartz mass.
Moisture Retention Properties
Understanding the transient nature of fluid migration associated, with the leaching of an unsaturated copper ore deposit, requires characterization of its moisture retentive properties (or moisture capacity). Insight into the copper ore moisture capacity can be gained through knowledge of the size and distribution of its interstices. In an unsaturated medium, hydraulic pore radii and/or hydraulic fracture aperture are reflected by variations in the pressure head which, in turn, causes changes in the saturation S or moisture content. The graphical expression is called the moisture retention, capillary pressure, or characteristic curve. The slope at any given point on the moisture retention curve represents the specific moisture capacity of the medium.
The functional relationship between saturation and water pressure head for the Casa Grande copper ore was derived using the mercury porosimetry method. Mercury porosimetry provides an indirect method for obtaining the moisture retention curve. A total of six mercury intrusion drainage tests were performed (three from each hole), and then adjusted to account for the differences between the properties of mercury and water for use in the fluid flow model (Friedel, 1991).
Pressure Head and Saturation
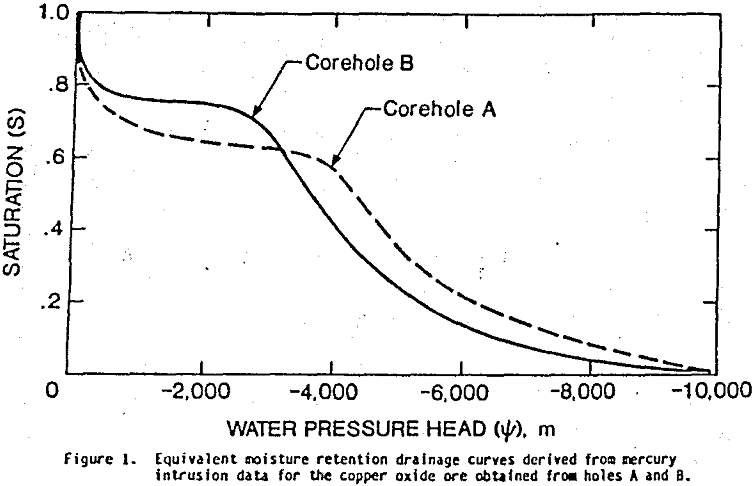
Figure 1 depicts 2 of the 6 water retention drainage curves derived from mercury intrusion data for the copper oxide core obtained from holes A, and B. These curves typify moisture retention properties characteristic of those sampled. Conformity of these retention curves (similar shape over the same range of pressure head) implies structural homogeneity over the distance spanned by these boreholes. Hence, any one sample would suffice for the analysis.
The shape of a drainage curve often reflects the relative homogeneity of the pore size distribution. If the pressure head remains constant over a large water saturation interval, the related pore dimension is considered homogeneous. Conversely, a variation in pressure head as a function of saturation implies that pore dimensions are relatively heterogeneous.
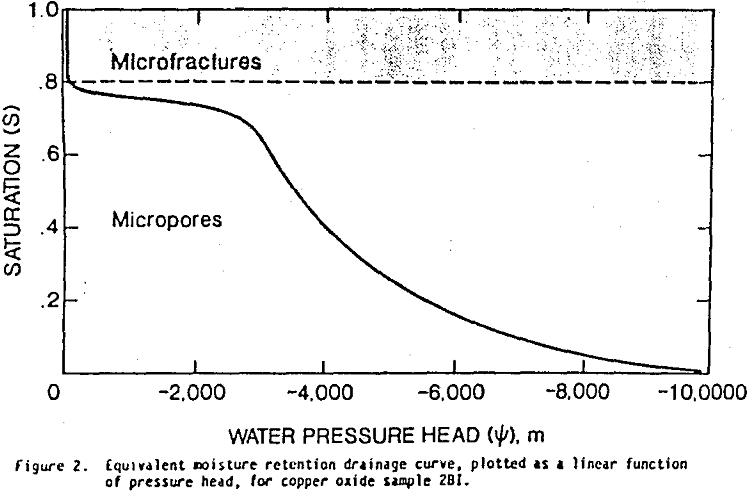
Figure 2 depicts the equivalent moisture retention drainage curve for a typical copper oxide sample. Two prominent pore distributions are obvious; the first reflects microfractures at low, negative pressure head values associated with relative saturation of 0.8095 to 1, while the other reflects micropores at pressure head values associated with saturations from 0 to 0.8095. These results are consistent with interpretations based on the axioplan and scanning electron microscope analyses observed earlier.
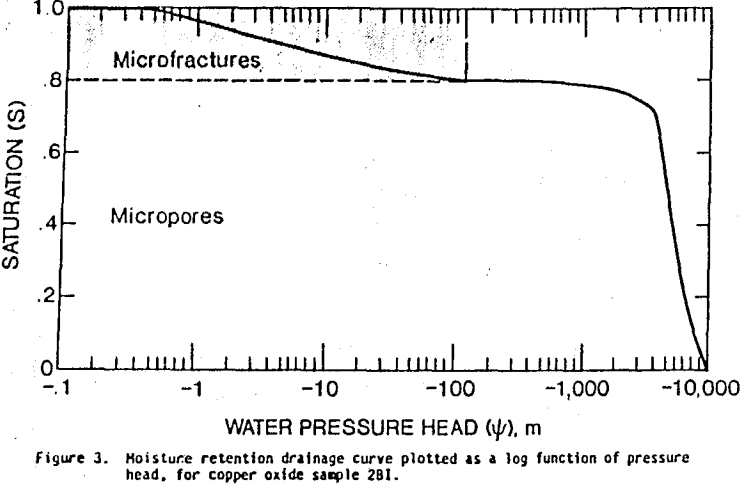
To better assess the range of pressure head values over which the saturation varies, the saturation is plotted against the log of pressure head (fig. 3). Micropores in the saturation range between 0.8095 to 0 are associated with pressure head values ranging from -150 m to -10,000 m; while saturation of microfractures between 0.8095 and 1 correspond to pressure head values of -150 m to -0.1 m, respectively. Test results at water pressure head values less than about -3,500 m should be considered inaccurate, because of the inability of the mercury intrusion method to penetrate micropores less than about 0.002 micron. This limitation is further reinforced because residual saturation does not, as expected, reach an asymptotic value slightly above zero (field capacity).
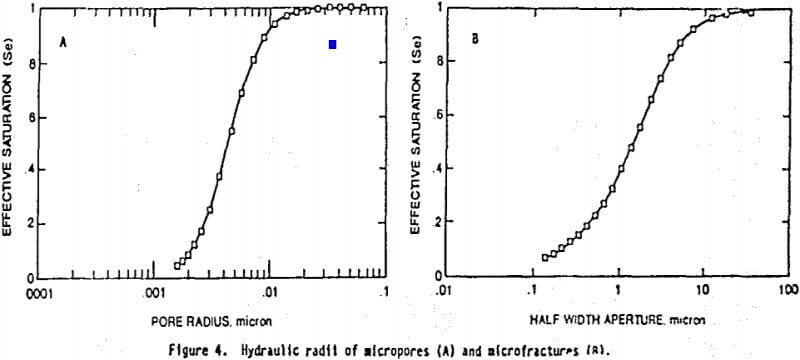
Hydraulic radii, reflecting the pore size distributions “seen” while draining (or drying), are calculated (Friedel, 1991) and displayed in figure 4. The microfractures appear to have the broadest pore size distribution (greatest slope) with hydraulic half width apertures ranging from 0.15 to 33 microns. The most uniform hydraulic half width aperture distribution exists between 1 to 4 microns which is consistent with that observed using the microscope. The hydraulic radii associated with the micropore distribution ranges from about 0.0015 to 0.05 microns; however, it is uniform between 0.0025 to 0.0075 microns.
Estimating the Hydraulic Properties
To be able to study the behavior of injection and recovery of leach solutions in an unsaturated setting, knowledge of permeability, or the hydraulic conductivity (also known as the coefficient of permeability, or capillary conductivity), and its relationship to moisture content is needed. The most direct way to obtain this relationship is by experiment. Reliable estimates of unsaturated hydraulic permeability are difficult to obtain, mainly because of difficulty in obtaining representative samples, and the time and expense involved. An estimate of the permeability function was obtained, however, from the moisture retention properties already discussed, i. e. saturation as a function of pressure head (Friedel, 1991). Although, fluid flow phenomena in partially saturated media normally involves two-phase flow of a wetting and non-wetting fluid, usually air and water, the flow of air is seldom of major significance. Hence, the present investigation is restricted to the permeability of the water phase only.
Several unsaturated permeability models have been developed that are based on probability functions describing the relationship between the measured moisture content and water pressure head. Using the Brooks and Corey (1966), and Brutsaert (1968) power functions, it was found that their two dependent parameters did not yield reasonable results for fitting the moisture retention curves associated with Casa Grande ore. On the other hand, the closed form expression developed by Van Genuchten (1980) seemed to provide reasonable results, requiring three dependent coefficients to be estimated.
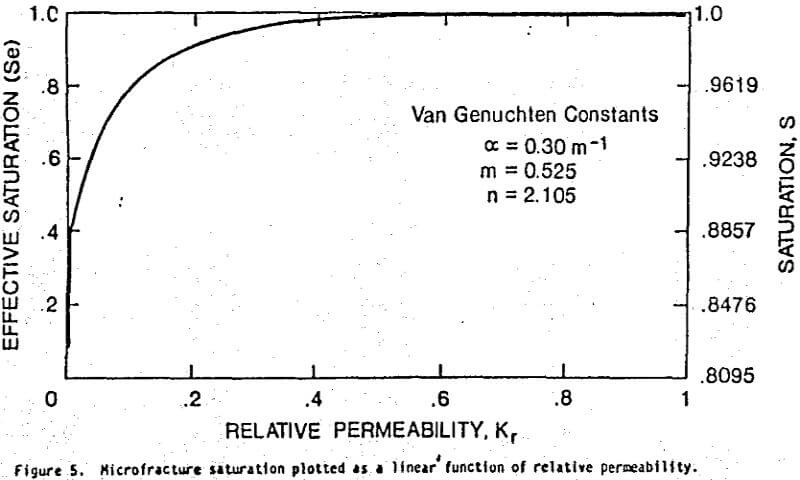
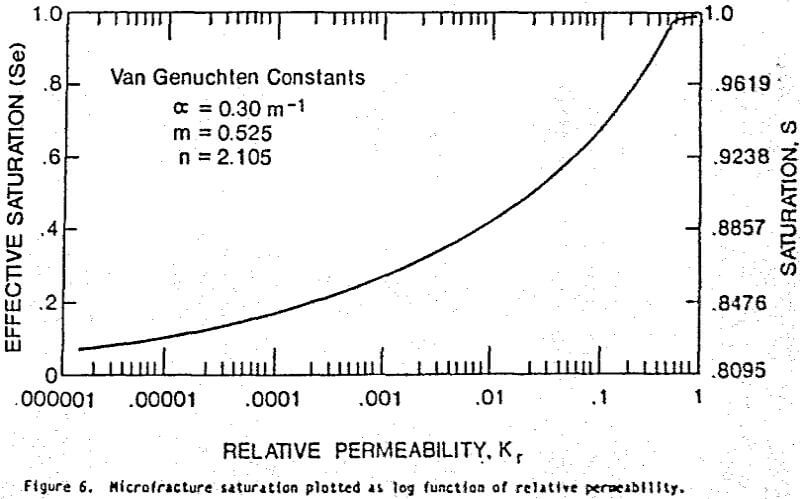
A plot of the nonlinear relative microfracture permeability distribution is presented in figure 5. This permeability function was calculated using the relationship outlined by Friedel (1991) and the Van Genuchten constants: α = 0.30 l/m, m = 0.525, and n = 2.105. It is noteworthy that permeability is nonlinear and observed to decrease one order of magnitude with a 20 percent reduction in saturation. Figure 6 depicts the saturation plotted as a log function of permeability. By inspection the permeability diminishes with decreasing saturation ultimately spanning 6 orders of magnitude. The maximum rate of permeability decrease for the Casa Grande ore occurs at saturations below 45 percent. Using the range of saturated permeability values, 10-² to 10-¹ md, corresponding permeability values in md can be obtained from the product of the relative permeability and saturated permeability. Assuming a best case, the range of permeability would be 10-¹ md (Se = Ss = 1) to about 10 -6 md (Se = 0, Sr = .8095). While the absolute permeability for the micropores can not be firmly established, it appears to represent the end of the microfracture continuum at about 10 -6 md. Therefore, fluid in micro-pores can be assumed to be immobile for the purposes of this study. Hence, the remaining portion of this study investigates only the fluid movement in the microfractures.
One obvious conclusion from the foregoing is that a decrease in saturation results in decreasing the permeability in the medium, and thereby inhibiting fluid flow. From an environmental viewpoint, leach mining in an unsaturated setting presents a tractable scheme under which luxiviants may better contained. From a production standpoint, however, this may require permeability enhancement by high pressure injection, hydrodilation, hydrofracing and/or in-situ rubblization. For either objective, site specific modeling is required to assess injection-recovery pressure requirements.
Hysteresis
Unsaturated porous media typically displays a hysteretic behavior. The two branches of the hysteretic loop (drainage and wetting) therefore “see” a different average effective pore size distribution, depending on whether the sample is being saturated or desaturated. Since the drainage branch exhibits higher moisture content than the wetting branch at any given pressure head, the porous media becomes more retentive during the drying cycle. Hence, the average effective pore size distribution during a drainage experiment shifts toward smaller values of pore radius than one for the wetting branch. This may, in part, explain why the half width apertures calculated from a drainage experiment are slightly less than those observed when using the microscope approach.
For modeling fluid flow from the injection well into unsaturated copper ore, knowledge of the wetting boundary curve is required. Since a mercury extraction curve was not obtained during porosimetry testing, an equivalent wetting boundary curve was not originally determined. The similarity hypothesis (Maulem, 1977) provided a means to derive the wetting boundary curve, based on knowledge of the drainage boundary curve.
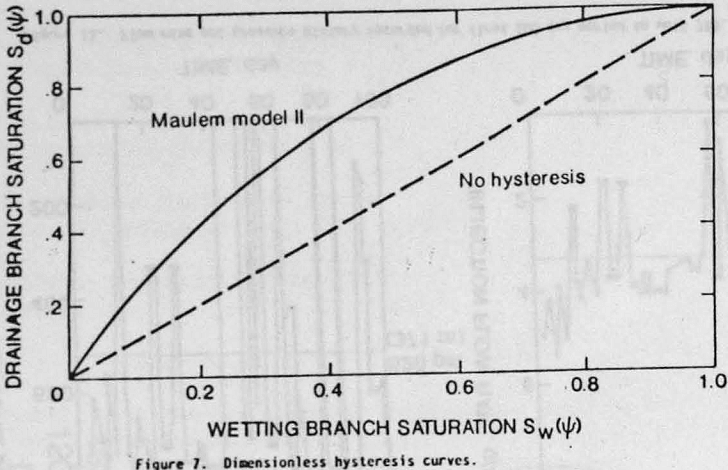
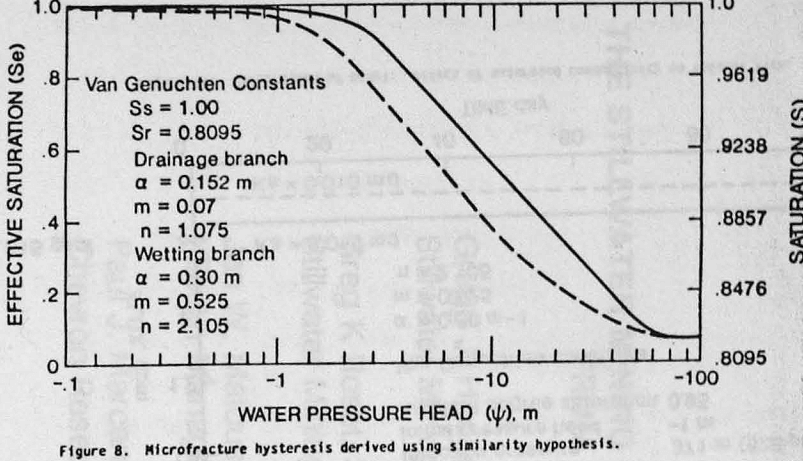
The dimensionless curves for the hysteretic Maulem model II, or for the case when hysteresis is not present is depicted in figure 7. When there is no hysteresis effect, a linear relationship exists and flow either drainage, or wetting, follows the same path. The Maulem model II, however, produces an expected departure from the straight line flow path. Since hysteresis is normally present in rock, it is incorporated in the finite element, unsaturated flow model. Figure 8 compares corresponding hysteretic loops for microfractures. Using the Van Genuchten approach, both the drainage and wetting branch constants could be calculated. These are summarized in table 2.

It is cautioned that the microfracture drainage curves, however, are suspect at pressures at or beyond about -3,500 m pressure head.
Computer Modeling of Underground in Place Leaching
Mathematical Model for Unsaturated Fluid Flow
Modeling the movement of water in a partially saturated porous medium has been discussed by many authors. A review of the state-of-the-art can be found in a recent text edited by Evans (1987). Basically, the movement of water must take into account the movement of liquid water, water vapor, air and the medium itself. The simplified approach taken here invokes the assumption of single phase flow. Hence, the water is considered mobile, while the air is assumed immobile.
An equation describing partially saturated and unsaturated flow of water in porous media, neglecting air-water interactions, can be derived by the principle of conservation of mass and the constitutive relationship given by Darcy’s law. This governing nonlinear, second-order partial differential equation is known as the Richard’s equation.
Finite Element Mesh and Flow Boundary Conditions
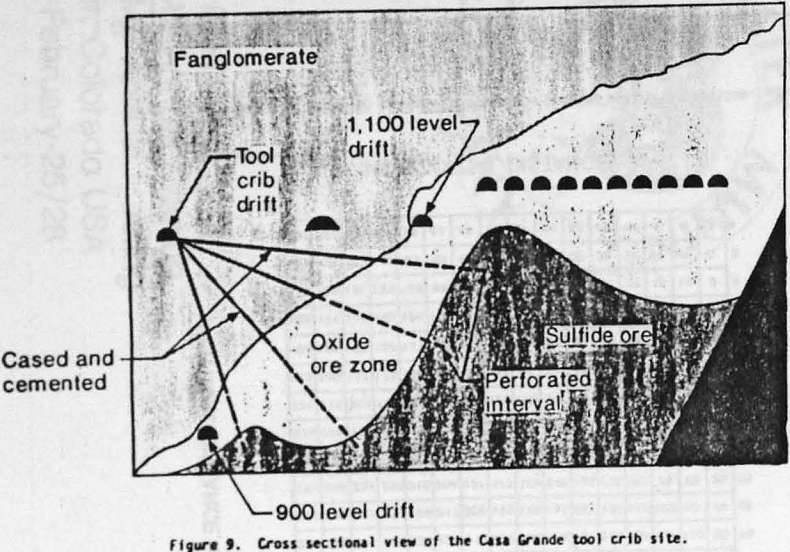
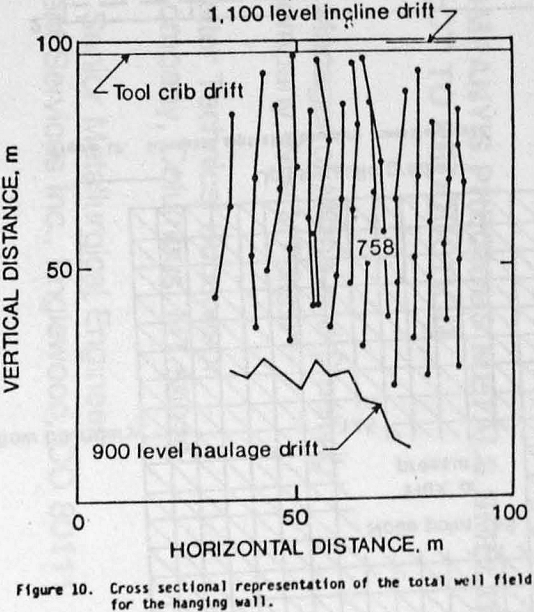
The nature of fluid flow is generally a 3-dimensional phenomenon, however, a 2-dimensional representation of the Casa Grande tool crib operation can be approximated by considering radial flow in the region perpendicular to a well. That is, we consider the surface that exists along the contact between the fanoglomerate (cemented gravels) and copper oxide ore (hanging wall). This surface undulates in cross section (fig. 9) but can be characterized in a 2-dimensional plan view by projecting each well onto this plane. This approach appears justified, since only the interval spanning the copper oxide ore is perforated. Figure 10 gives a cross-sectional representation of the total well field for the hanging wall. Wells related to a given fan pattern are depicted by connecting each group of wells by a solid line.
The corresponding finite element grid for the hanging wall cross section is given in figure 11. The FE solution domain is represented by a 100 m x 100 m mesh with 512 simplex triangular elements and 300 corresponding node points. The x-direction represents the horizontal distance along the tool crib drift, while the y-direction denotes the vertical distance along the hanging wall. The lower, left-hand corner represents the 0 m, 0 m mesh coordinate, and the upper, right-hand corner represents the 100 m, 100 m coordinate. The distance between any horizontal or vertical pair of node points is 6.25 m. The complete modeling domain was chosen to be large enough so that there would be no interaction between boundary conditions associated with its surface and sides. If interactions exist, the calculations of both pressure and flux would be inaccurate.
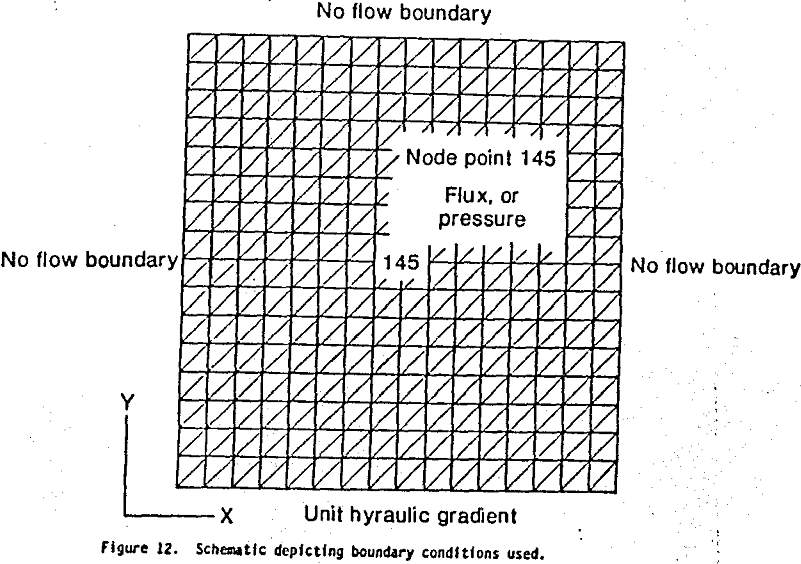
The boundary conditions employed for the site specific simulations included no flow at the upper and side boundaries, a unit hydraulic gradient along the lower boundary, and a point source or sink at the interior of the mesh.
Injection and/or recovery is assumed to occur at node point 145, the center of the mesh. A schematic depicting these boundary conditions with respect to the finite element mesh is shown in figure 12.
Inverse Modeling
Since the Casa Grande tool crib site is known to have macroscale fractures linking various wells (Schmidt, 1990), it is necessary to identify a “tight” well. A “tight” well, defined as one that had minimum observed flow rates, is used to represent fluid flow through the rock matrix. Since the Casa Grande site has had extensive permutations in pressure conditions over a 1-year period, an additional requirement is to select an interval from the onset of leaching to the first permutation in well conditions.
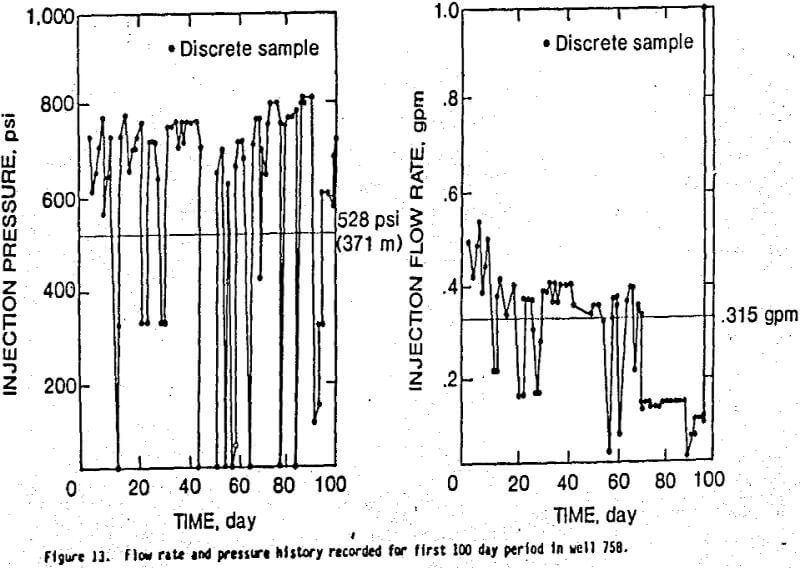
Figure 13 depicts the flow rate and corresponding pressure history recorded for the first 100 day period in well 758. The mean flow rate and injection pressure are calculated to be 0.315 gpm and 528 psi, respectively. These values are used during subsequent inversion of the FE model to determine the appropriate saturated permeability and ambient degree of saturation.
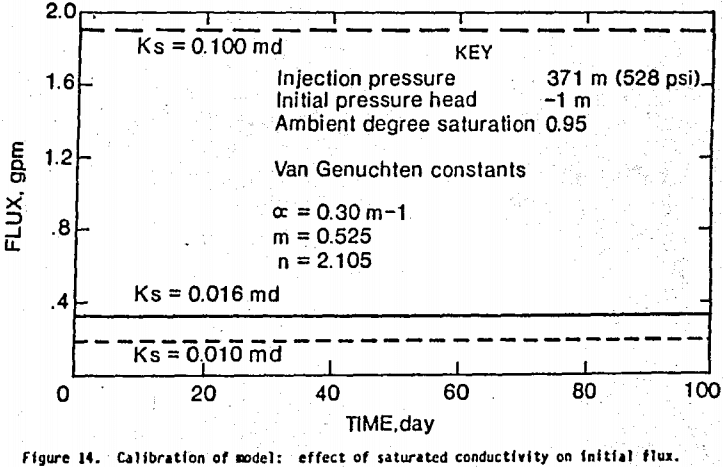
The first inversion involved calibrating the model by adjusting the saturated permeability until the computed initial flux matched that observed in the field. Figure 14 gives flow rate (flux) for a range of saturated permeability values. The maximum permeability of 0.1 md resulted in a maximum flow rate (1.92 gpm), while the minimum value of 0.01 resulted in a minimum flow rate (0.19 gpm). A saturated permeability value of 0.016 md matched the flow rate (0.315 gpm) observed in well 758. This agrees with the value 0.0177 md from the using a geostatistical analysis used to estimate permeability. The in situ permeability estimate obtained from well 758 (0.016 md) also matches that obtained from core samples.
The second simulation involved estimating the ambient degree of saturation by direct inversion. The ambient degree of saturation is defined as that saturation which existed prior to in situ leaching. Estimating the ambient degree of saturation was accomplished by perturbing the initial pressure condition until the transient pressure response matched the results observed in well 758, i.e. where injection pressure was equal to 371 m at the 100th day. The initial pressure head condition (zero time) was decreased incrementally beginning with 0 m until transient pressure conditions were matched (fig. 15). The -1 m initial pressure condition corresponds to an ambient saturation of 95 percent.
Since laboratory moisture determinations were not available, it was not possible to verify this ambient degree of saturation. An alternative approach was used, however, to qualitatively check the calculated minimum saturation, based on draining the initially saturated domain over a large time period. From the 1,000 year simulation based on the Van Genuchten microfracture drainage constants, a permeability of 0.016 md correspond to a minimum effective saturation of about 88 percent. The gravity effect is clearly evident from the moisture tongue in the center of the figure 16, demonstrating that, at least qualitatively, the derived ambient degree of saturation appears realizable.
The effect that the tool crib, and other drifts at the 900 and 1100 levels, have on fluid distribution in the rockmass is shown in figure 17. These results portray a 25-year simulation approximating the time since these drifts were created. This analysis was necessary to assess whether the boundary conditions associated with these drifts would need to be integrated into the forward model. Van Genuchten constants again reflect the drainage curve, with a saturated permeability of 0.016 md and ambient degree of saturation of 95 percent. The effect of imposing drifts essentially increases the moisture gradient in a region of about 2½ times the radius of each drift. The regional effect on ambient degree of saturation, however, is largely unaffected.
Forward Modeling
The primary purpose of transient unsaturated flow modeling is to provide insight into the hydrologic design of in situ leaching operations in deposits where copper mineralization is disseminated in segmented blocks of ore. Forward (predictive) modeling is performed using TWOD with reference to a single injection or recovery well drilled into a homogeneous block of ore, or equivalently with reference to a single linear fracture which acts as a source or sink for a single block of ore. Well 758 is seen as an example of a well in the tool crib pattern that is drilled entirely within a single ore block.
Values of ambient degree of saturation (95 percent), and saturated hydraulic permeability (0.016 md) derived during the inversion process, and those Van Genuchten constants previously described, were used to simulate fluid flow in forward modeling. The effect of injection pressure on the transient build-up of a saturated plume in an ore block is shown in figure 18. For early analysis of plume development, the solution domain was reduced to 25 m by 25 m, corresponding to a internodal distance of 1.56 m, while using the same mesh (fig. 11) and boundary conditions (fig. 12).
Flow simulations demonstrate that an injection pressure of 1500 psi (currently the practical limit at the tool crib site) sustained for about a 150 day period is required before a circular block of ore with a radius of 5 m becomes completely saturated. The hydraulic head (elevation head plus pressure head), pressure head, and fluid distribution for an injection source (such as well 758) after a 1 year period, while subjected to an injection pressure of 1500 psi, are given in figure 19. The symmetry of the pressure plume in these figures reflects the assumption of homogeneous and isotropic conditions within an ore block. The steepness of the cone is attributed to the large moisture gradient existing about the source. While lesser pressures could be employed, the waiting period for solution penetration would be correspondingly longer. Pressures at or below 500 psi would effectively contain solution within a 2.5 m radius around the injection source.
Converting the injection source after a 1 year period to a recovery sink, with a zero gage pressure or a negative (suction) pressure affects the head and fluid distribution, as shown in figures 20 and 21. In each case, the pressure plume around the sink is reduced. The square surface at an effective saturation (Se = 1) in figure 20 is an artifact produced by the contouring package. This is in reality a cone with a diameter equal to slightly less than the length of its side.
Since the zero gage pressure would not be less than or equal to the microfracture air entry value (about -4 m), only 1 percent of the injected solution can be recovered by the sink. The bulk of the solution remains captive in the rock by capillary tension. Because of the capillary effect, a dramatic increase in solution recovery, i.e. about 95 percent, can be achieved by inducing a suction head of -10 m at the sink as shown in figure 22.
Hydrologic Design
Forward modeling shows that solution penetration into ore blocks can be achieved, despite the reduced permeability associated with unsaturated conditions, if well injection pressures are of sufficient magnitude. From an operational standpoint, if the target ore zone were a single homogeneous ore block, a flux rate of .05 m/day would be unacceptably low. At the closest spacing, wells in the tool crib pattern are 5 m apart.
The observed breakthrough times for flow of solution between injection and recovery wells at the tool crib site ranges from 1 to 150 hours, after the start of injection, indicating that the network of macrofractures which transects the target ore zone is, initially at least, the dominant flow path through the ore zone.
A hydrologic design suggested by the results of forward modeling is a variant of the push-pull test method. Injection in a core region of the tool crib wells at pressures of 1500 psi is maintained for 30 to 60 day period. The injection interval serves to completely saturate the ore blocks and build pressure in the saturated macrofracture network. Following the 30 to 60 day interval wells are selectively converted from injection to recovery mode. Suction pressure is applied, if practical. Otherwise, the lowest possible head condition should be imposed. To ensure that there is ample residence time to load the injected leach solution with copper, and that the sorption of copper, and/or precipitation of gangue minerals does not occur, flow rates during recovery can be regulated by shutting in the well to some degree. The advantage of applying back pressure in the well is to prevent the established pressure plume from dissipating too rapidly. The concentration of copper and gangue minerals in solution would need to be continuously monitored to adjust recovery flow rates.
A hydrologic design involving rubblization of a mineralized zone could be expected to improve fracture permeability in the ore zone by orders of magnitude. Rubblization conducted in a manner similar to that used for in situ oil shale retorting ts just one possibility. A factor of central importance for determining the desired degree of rubblization (or the average block size) is the penetration rate of leach solution into unsaturated ore blocks.
Forward modeling suggests that maintenance of injection pressures of 500 psi, or below, would effectively confine solutions to a rubblized zone in which the average block radius of 2 m or less. Flow in blocks larger than this, on the periphery of the rubblized zone, would be effectively impossible in the absence of large-scale fractures or sinks, under the permeability constraints imposed by a partially saturated setting. The undisturbed (and unsaturated) rock would therefore serve to confine the solution plume within the rubblized zone, providing a safeguard against environmental contamination.
Conclusions
The Casa Grande copper oxide deposit is characterized as a variably-saturated tri-modal porosity system. A network of macrofractures segment the copper ore into blocks which have a bimodal porosity distribution including micro-fractures and micropores. Once the macrofractures are saturated they act as a source/sink to these ore blocks.
Moisture retention characteristics indicate that a microfracture-micropore permeability continuum exists in the rock blocks. The microfracture permeability diminishes non-linearly with decreasing saturation, spanning 6 orders of magnitude; hence, fluid flow in the saturated micropores is essentially immobile. Since the microfractures provide internal access to copper-hosted minerals, the unsaturated condition (ambient saturation of 95 percent) will be the dominant control on flow capacity.
Forward modeling demonstrated that solution penetration into ore blocks can be achieved, despite the reduced permeability associated with unsaturated conditions, if well injection pressures are of sufficient magnitude and time permits. Post injection-recovery simulations demonstrated, however, that the bulk of solution injected at 1500 psi for 1 yr (roughly 98 per-cent) is held captive in the rock by capillary tension, when using the conventional air lifting technique. Conversely, inducing a suction head of -10 m (air entry value -4m) for a two-week period immediately following the injection period increases the capacity to recover leach solution (roughly 95 percent). By specifying proper time and pressure constraints, forward modeling can be used to optimize a mine design by determining the maximum block diameter to be derived through rubbilization. Upon rubbilizing a zone to an average block diameter of 4 m, and sustaining an injection pressure of 500 psi for a 100 day period, leach solution could be distributed effectively at the Casa Grande copper oxide tool crib site, while inhibiting flow outward into the surrounding rock mass.