In previous topics, we’ve discussed strengths of materials because failure typically occurs when stresses exceed the strengths, it is important to know the stress distribution in a ground close to an opening, for example.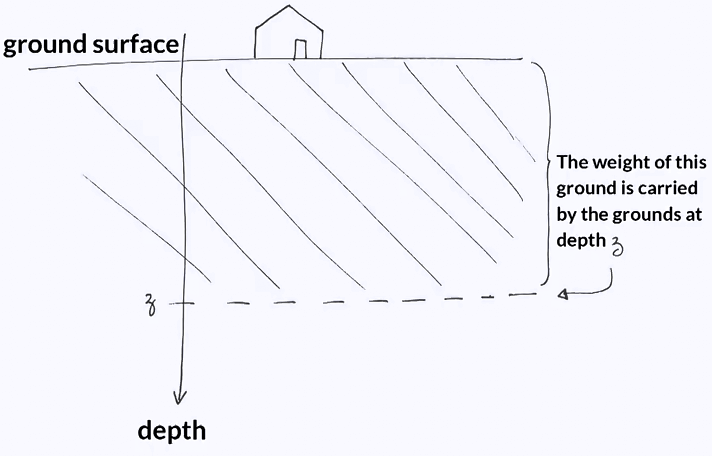
This will be the topic of this module, but first, let’s consider vertical stress. To some extent, this represents at a certain point in the ground how heavy all the material above the point is. In this photo, we can see men carrying layers of tea packs and you can easily imagine that the higher the pile of tea packs, the heavier the load to carry.
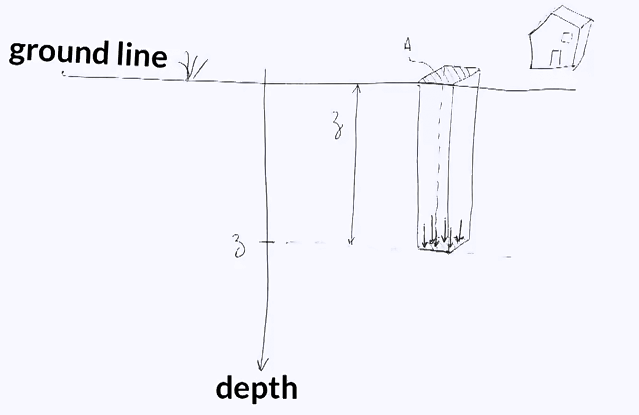The same thing occurs in the ground. The ground at a depth Z carried the weight of all the ground above it. The deeper we go, the more ground there is to carry, and the higher the vertical stress. More specifically, the vertical stress, noted sigma V, I calculated as the weight of a column of ground divided by the cross-sectional area of the column. Estimating the weight of the column of ground requires knowing its unit weight, noted gamma and expressed in kilo newton per cubic meters. For rocks, gamma typically ranges from 20 to 35 kilo newton per cubic meters. For a flat ground and a homogeneous rock mass without external loading, the vertical stress at a depth Z can simply be expressed as the unit weight times the depth Z. the presence of external loading for example, the weight of a building creates additional stress in the ground that dissipates with depth.
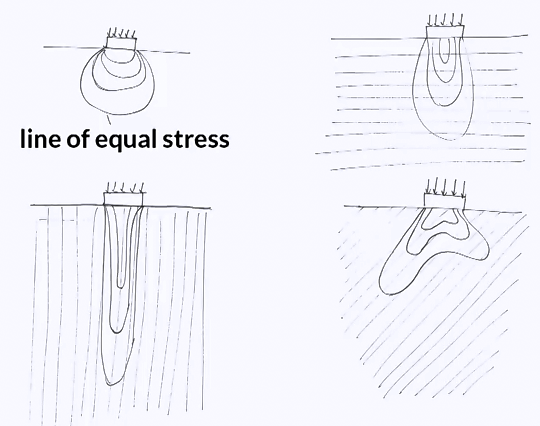
The stress state in a rock mass also includes horizontal stresses. These are the results of complex geological processes, loading history, temperature, or tectonic activity. See, for example, this figure that shows the different type of interaction between tectonic plates to which corresponds different distribution of stress. For revers and strike slip faults, the horizontal stress, at least in one direction, is larger than the vertical one. There is another element to account for when determining stress distribution in the ground. The presence of discontinuities does affect the distribution of stress.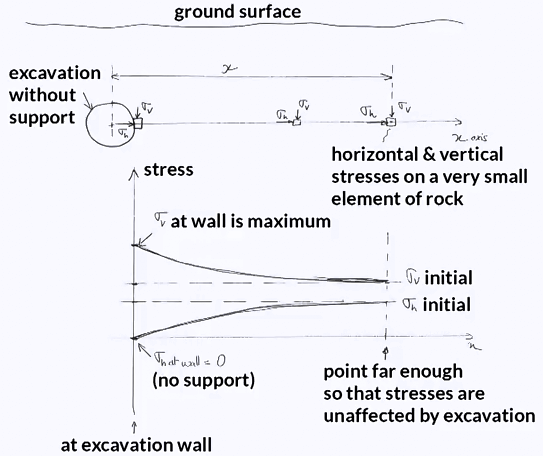
This figure shows the lines of equal stress values in the ground resulting from the application of a load at the surface. We see how the presence and orientation of the discontinuities can modify the distribution of stress. So in a heterogeneous rock mass, determining the stress distribution is often more difficult than in a homogeneous ground. Engineers also have to predict how modifying the rock mass for example, by building on it or excavating it affects the stress distribution in the ground.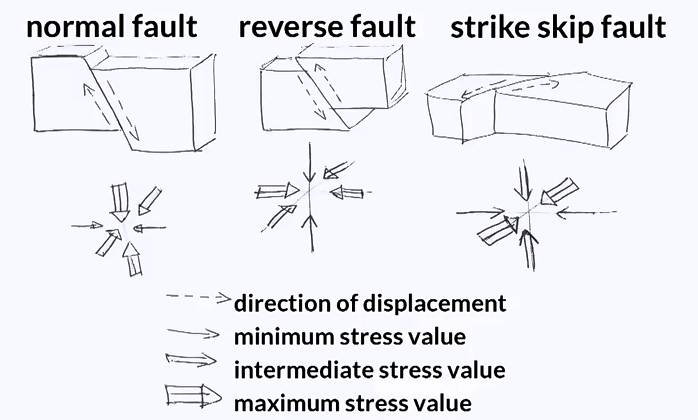
For example, creating an opening, especially without internal support, does affect significantly the stress distribution in the ground. We will see this in this figure. Far from the opening, the stresses are largely unaffected by excavation and equal to their initial value, but as we got closer to the excavation, the vertical stress increases, and the horizontal stress reduces. If the rock mass is strong enough, this increase in vertical stress will not lead to failure. The role of engineers is to predict the evolution of vertical and horizontal stresses in a rock mass when working on that rock mass and ensuring that the rock mass does not fail or failure is controlled.
https://youtu.be/h5rqCs60E-g