The transfer of kinetic energy of translation into other forms of energy by impact is a fundamental process in most crushing and grinding operations. During and after the impact process the original source energy may be accounted for in any of the following possible forms:
- Kinetic energy of translation of both the impacted and impacting objects.
- Kinetic energy of vibration of the components of the impact system.
- Potential energy as strain energy of the components of the system or in the form of residual stresses.
- Heat generated by internal friction during plastic deformation or during damping of elastic waves.
- New surface energy of fractured materials.
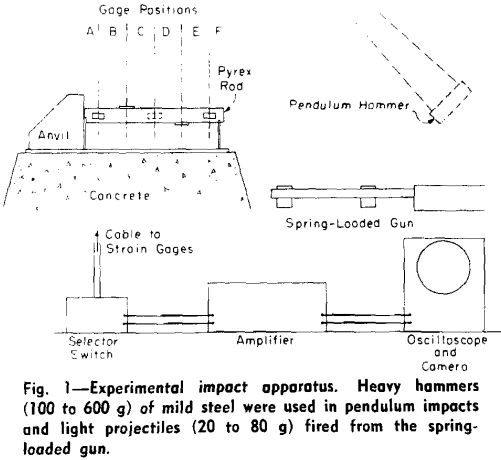
Experimental Method: Longitudinal impact of a rod with a fixed end was chosen as the impact system for investigation. The rod was mounted horizontally and the fixed end was formed by butting one end of the rod against a rigidly mounted steel anvil. The rod, of pyrex glass, was 10 in. long by 1 in. diam with both ends rounded to a 6 in. radius. The rounded ends permitted reproducible impacts on the free end of the rod and assured a symmetrical fixed end. Pyrex was selected as the rod material because of the marked elastic properties of such glass and the similarity of fracture between pyrex and many materials encountered in crushing and grinding operations. The frequency of natural longitudinal oscillation of the rod was 10 kc, and thus simple electronic equipment could be used for observation of strain changes occurring in the rod at this frequency.
Determinations of the kinetic energies of translation prior to impact were made in the case of the pendulum hammers by measuring the height of fall of the hammer and in the case of the projectiles by measuring the exit velocity from the gun barrel by means of an electrical circuit employing light sources, slits, and phototubes.
Experimental Results
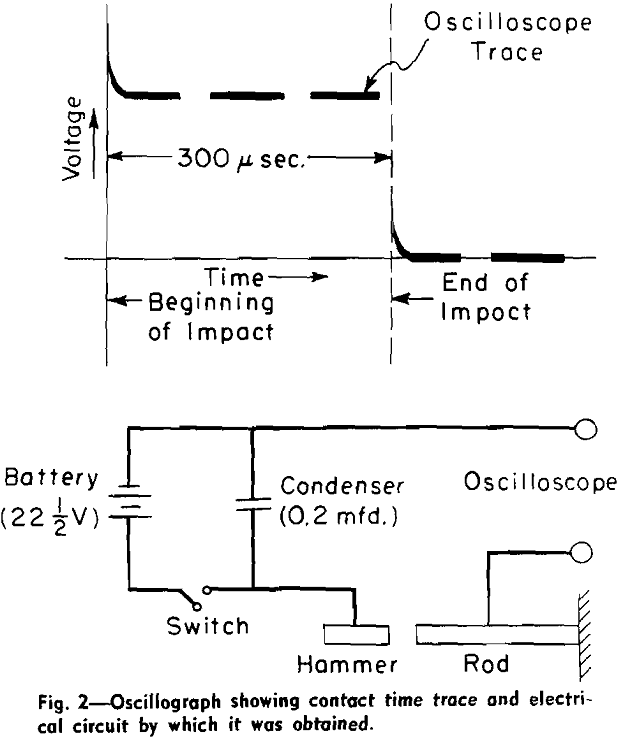
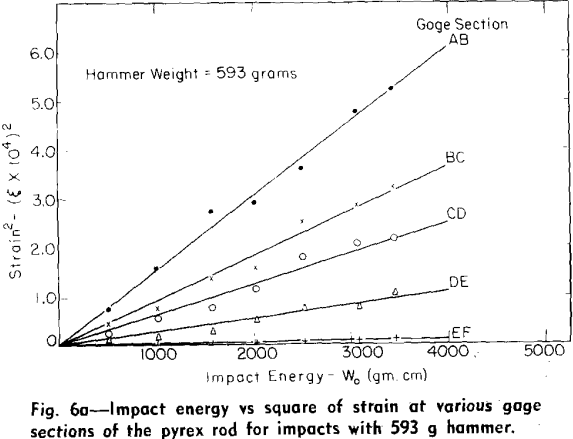
The immediate aim of the experiments was to determine the strains at various sections of the rod as a function of the impacting kinetic energies of the hammers, the Young’s Moduli of the glass, and the durations of impact. Data for determination of all the above quantities were obtained in the form of oscillographs.
The oscillographs from the impact tests showed voltage-time relationships which were obtained from the amplified signals of the strain gages. The most important measurement taken from each voltage-time oscillograph was the voltage value at the instant when the bar had absorbed the greatest amount of strain energy during a particular impact. To locate this instant the following procedure was adopted.
From Hooke’s Law the strain energy at a point in an object under simple compression or tension is proportional to the square of the strain at that point. An analysis of plots of the square of the strain at various gage sections of the impacted rod as a function of time showed that maximum strain energy absorption took place when the maximum elastic deformation developed at one section of the rod was greater than that developed anywhere else in the rod at any time during the impact process. Voltage measurements for the calculation of the maximum strain energy absorbed for a particular impact were made, therefore, on each set of five voltage-time traces at the time when maximum elastic deformation occurred; the latter condition was indicated by a maximum vertical response on one of the five voltage-time traces.
Effect of Hammer Weight on Strain
The occurrence of two peaks indicates that during the overall time of impact the rod received two separate blows, one following the other so rapidly that with¬out sensitive methods of detection the impact would appear as one blow. The multiple blow effects were obtained when hammers weighing more than 200 g were used for the impacts on the pyrex rod.
It will be shown that the time during which the impacting objects remain in contact is dependent on the mass of the hammer in such a manner that the heavier the hammer the longer the contact time. Mason has shown that with contact times long compared to the period of fundamental oscillation of an impacted system the oscillations of the system modify the force developed at the point of contact in such a manner that it may consist of a series of blows. In this investigation, hammer weights 200 g and greater gave rise to impact times longer than the period of fundamental oscillation of the rod, and the forces developed at the struck end of the rod by these hammers showed more than one peak value
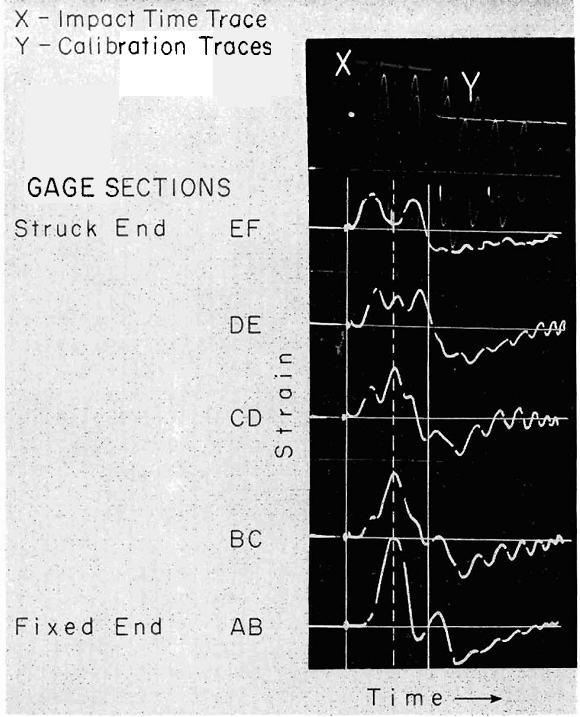
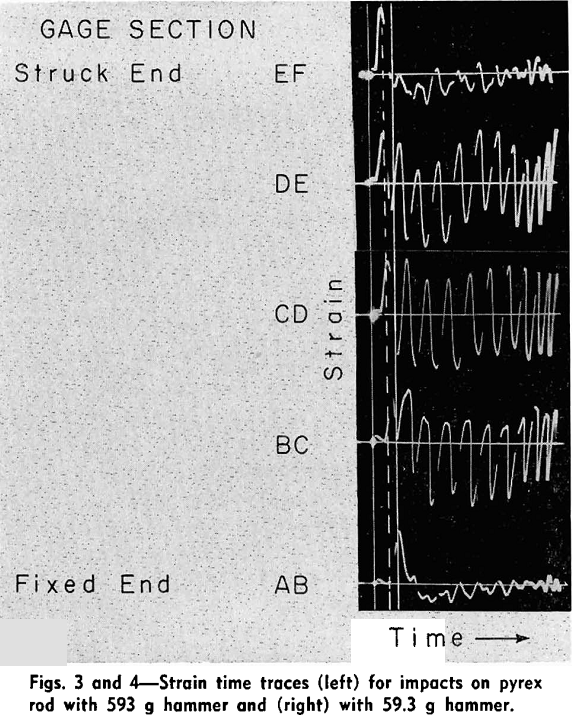
during the time of contact. On the other hand, the times of contact for impact hammers weighing less than 100 g are shown, in the next section, to be less than the period of fundamental oscillation of the rod. In these cases the rod oscillations were not excited soon enough to modify the contact forces to any great extent and the traces for the struck end of the rod showed only one symmetrical peak during the time of contact.
Strain vs Time After Impact: An interesting effect can be observed in the strain-time records in regard to the amplitude of vibration of the rod after the impact has been completed. When the hammer rebounds after impact the rod continues to oscillate and, since both ends of the rod are free, the oscillation is essentially a harmonic vibration at the fundamental frequency of the rod. Under longitudinal harmonic oscillation all points of the rod pass through their equilibrium positions at the same instant and thus the signals from the various strain gages are in phase.
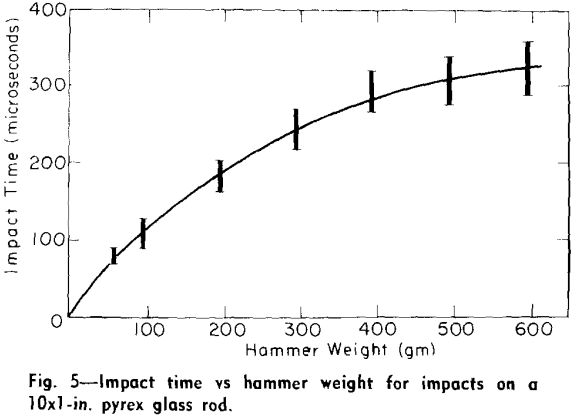
Effect of Hammer Weight on Time of Impact: Fig. 5 shows the experimental relationship obtained between the measured contact times of the hammers and rod and the weights of the hammers used in the impacts. Each of the solid vertical lines in these figures indicates the variation of the measured values for the impact times of any single hammer weight. Since the relative variation of the measured values of impact times increased with hammer weight the data are presented as varying over ranges rather than as single points representing averages of the experimental measurements.
Discussion of Results
The experimental results from this investigation provide data for analysis of the loading forces which are derived from impact on a glass rod and for calculation of the maximum amounts of energy which are transformed from kinetic energy of impact to strain energy of the rod during impact. The data are also used to illustrate the effect of the mass of the impacting weight and the time of impact on the energy transfer process during impact.
Determination of Transfer of Kinetic Energy of Impact to Strain Energy: In the impact process when the hammer is decelerated to zero velocity all
its original energy of translation has been changed to other forms and the strain or potential energy of the hammer and rod system is at or near maximum. As the impact continues, the strain and vibrational energy of the system is partially reconverted to kinetic energy of translation of the hammer and rebound occurs.
The only form of energy that is directly usable in a comminuting or fracturing process is the strain energy that has been momentarily stored in the rod and the hammer. The experimental data of this investigation permit calculation of the maximum amount of strain energy absorbed by the rod. This maximum strain energy can be expressed as a fraction of the total kinetic energy of impact. 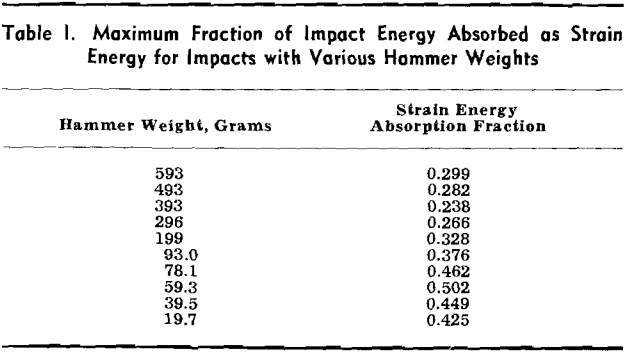
From the experimental results as summarized above a number of general conclusions may be made as to the application of the impact studies to comminution. The most obvious conclusion is that if kinetic energy is to be most efficiently utilized in an impact process for size reduction, the time of impact should be as short as possible, for all practical purposes, and the intensity of impact as large as possible. The former condition assures a substantial transfer of kinetic energy to strain energy and the latter condition assures the development of stress values sufficient to initiate and propagate fractures.

