Table of Contents
Gold occurs in nature chiefly as metal. It always contains more or less silver, and, in alluvial sands, may be associated with platinum and iridium. Gold is insoluble in hydrochloric or nitric acid, but is dissolved by aqua regia or by solutions of iodine, bromine, or chlorine. It is taken up by mercury, forming an amalgam, from which the mercury may be driven off by heat.
When gold occurs in particles of any size, it is readily detected by its appearance, but when finely disseminated through a large quantity of rock, it is separated and detected by the amalgamation assay—described below—or by a process of washing somewhat similar to vanning, or by the following test:—Powder and, if necessary, roast 50 to 100 grams of the ore, put on it three or four crystals of iodine and enough alcohol to cover it; allow to stand for half an hour; a piece of filter paper moistened with the liquid and burnt leaves an ash with a distinctly purple tint if any gold is present. It is better, however, to filter off the solution, evaporate, and ignite. Then, either take up with mercury, and ignite the amalgam so as to get a speck of the metallic gold; or treat with a few drops of aqua regia, and test the solution with stannous chloride : a purple coloration indicate gold.
AMALGAMATION ASSAY
This does not attempt to give the total produce of gold, but rather the quantity which can be extracted on a large scale; therefore it should imitate as closely as possible the process adopted in the mine or district for extracting the metal.
Take 2 lbs of the ore in powder and roast; make into a stiff paste with hot water and rub up for an hour or so with a little mercury. Wash off the sand carefully, and collect the amalgam. Drive off the mercury by heat, and weigh the residual gold. It is best to cupel it with lead before weighing.
In an experiment on a lot of ore which contained 0.189 of gold, 0.179 gram was obtained by the above process, equal to about 94½ per cent, recovered. With ores generally, the yield may be from 80 to 90 per cent, of the actual gold present.
DRY ASSAY
The dry assay of gold ores resembles in its main particulars the dry assay for silver by the crucible method; and for much that is of importance in its discussion the student is referred to what is written under Silver on pp. 90-113.
Size of Assay Charges
Gold ores rarely contain more than a few ounces, often only a few pennyweights of gold to the ton; consequently, the button of gold obtainable from such quantities of ore as may be conveniently worked by assaying methods is often so small as to require more than ordinary care in its manipulation. One milligram of gold forms a button of about the size of one of the full-stops on this page, and compared with a million similar particles of quartz (about four ounces), represents a produce of a quarter of an ounce to the ton : a proportion such as the assayer is frequently called on to determine. It is evident, therefore, that a charge of half an ounce or less of the ore, such as is usual with silver ores, would demand of the worker both skill and care in the handling of the minute quantity of gold to be obtained from it. Fortunately the work is simple and precise, so that in practised hands and with only a 5-gram charge the assay of a 5-dwt. ore is practicable; with so small a charge, however, the result is barely perceptible on a sensitive balance: the button of gold should be measured under a microscope. It follows, therefore, that larger charges of say 50, 100, or even 200 grams, have an advantage in that they lessen the strain on the worker’s attention, and, except in the case of the poorest mineral, bring the button of gold within the scope of the balance. On the other hand, the inconvenience of the larger charges lies in the amount of fluxes and consequent size of the crucibles required to flux them.
Sampling
A further consideration in favour of the larger charges is the matter of sampling. In preparing his ore, the student should ask himself what reasonable expectation he has that the portion he puts in the furnace will be of average richness. The larger charges are likely to be nearer than the smaller ones to the average of the parcel of ore from which they are taken. In explanation of this, let us suppose a large heap of 5-dwt. ore, in sand of the coarseness of full-stops, and containing all its gold in particles of 1 milligram, as uniformly distributed as care and labour in the mixing can accomplish. Such a heap could not possibly occur in practice, but it will serve for purposes of illustration. Now, one ton of the sand, however taken, would contain appreciably the same quantity of gold as any other ton. For a ton would contain about 8000 particles of gold; and even if two separate tons differed by as much as 100 particles (which they are just likely to do), this would mean only a difference of 1 or 2 grains to the ton. On the other hand, two portions of 14 lbs., which should contain on the average 50 particles of gold, are likely enough to differ by 10 particles, and this, calculated on a ton, means a difference of 1 dwt. It is easy to see that something like this should be true; for on calculating the 14-lb. lot up to a ton, the deviation from the average, whatever it may be, is multiplied by 160; whereas, if the ton were made up by adding 14-lb. lot to 14-lb. lot, up to the full tale, then a large proportion of the errors (some being in excess and some in defect) would neutralise each other. An average which is practically true when dealing with thousands, and perhaps sufficiently exact with hundreds, would be merely misleading when applied to tens and units. Reasonable safety in sampling, then, is dependent largely on the number of particles of gold in the charge taken, and the risk of an abnormal result is less, the larger the charge taken.
By doubling the charge, however, we merely double the number of particles. Powdering finely is much more effective; for, since the weight of a particle varies as the cube of the diameter, halving the diameter of the particles increases their number eight-fold. If, now, we modify our illustration by assuming the particles to have only one-sixth the diameter of a full-stop (which would represent a powder of a fineness not unusual in ores prepared for assaying), we should multiply the number of particles by 200 (6x6x6 = 216). We should then reasonably expect a 14-lb. parcel of the powder to give as safe a sample as a ton of the sand would give; and portions of a size fit for crucible work, say 50 or 100 grams, would be as safe as 10 or 20-lb. samples of the coarser stuff. For example, 60 grams of such powder would contain, for a 5-dwt. ore, about 100 particles; and in the majority of cases the error due to sampling would be less than 10 or 12 grains to the ton, and would only occasionally exceed a pennyweight. With richer ores the actual deviation stated as so much to the ton of ore might be greater, but it would represent a smaller proportion, stated in percentage of the gold actually present, and would ultimately fall within the limits of unavoidable error.
It will be seen that the size of the quartz particles has no direct bearing on the argument; and, in fact, the coarseness of the quartz only interferes by preventing the uniform mixing of the sand and by binding together several particles of gold; in this last case, particles so united must, of course, count as one larger particle. Now, there are some natural ores in which the gold particles are all very small; with these fine powdering and mixing yields a product from which a sample may be safely taken. Then, again, in “tailings,” before or after treatment with cyanide, we have a similar material, inasmuch as the coarser gold has been removed by previous amalgamation. With these, it is not unusual to take the portion for assay without any further powdering, since they are poor in gold, and have already been stamped and passed through a sieve of say thirty holes to the inch (linear).
But there are other ores, in lump showing no visible gold, which contain the gold in all possible degrees of fineness, from say prills of a milligram or so down to a most impalpable powder. The treatment of these cannot be so simple and straightforward. Suppose a parcel of 1000 grams (say 2 lbs.) of such ore in fine powder, containing on an average 1 particle of 1 milligram (the presence or absence of which makes a difference of .6 dwt. on the ton), 10 others of about .5 milligram (each representing .3 dwt.), and 100 others, which are too coarse to pass through an 80 sieve, and having an average weight of .1 milligram (each .06 dwt.), and that the rest of the gold, equivalent altogether to 2 ounces to the ton, is so finely divided that a charge of 50 grams may be taken without any considerable risk of its interfering with the sampling. Then in a 50-gram charge there would be one chance in twenty of getting the milligram particle, in which case the result would be 12.35 dwts. too high; on the other hand, if it were not present the result would on this account be .65 dwt. too low. Of the ten .5-milligram particles, it is as likely as not that one will be present, and its presence or absence would cause an error of 3.3 dwts., more or less. Of the 100 particles of .1 milligram, there would probably be from 3 to 7, instead of 5, the proper number; this would mean a variation of 2.6 dwts. from the true proportion. So that the probable result would range about 5 dwts. more or less than the 2½ ozs., which is the true produce, and there are possibilities of astounding results. It is true that the majority of the results would be well within these limits, and now and again the heart of the student would be gladdened by a beautiful concordance in duplicate assays; nevertheless, there can be no reasonable expectation of a good assay, and to work in this way, on a 50- gram charge, would be to court failure. The coarse gold must ruin the assay.
The difficulty may be met by concentrating the whole of the coarse gold in a small fraction of the ore, by sifting and making a separate assay of this fraction. A portion of the ore, of about 1000 grams, is ground to a very fine powder and passed through an 80 sieve, re-grinding when necessary, until only 20 or 30 grams is left of the coarser powder. This is mixed with fluxes and carried through as a separate assay. The sifted portion is thoroughly mixed, and a portion of it, say 30 or 50 grams, taken for assay. The weights of the two portions must be known, and care must be taken that nothing is lost in the powdering. The method of calculating the mean result from the two assays is shown on page 109. In this way of working there is no advantage in continuing the grinding until the coarser fraction is reduced to a gram or so—rather the contrary; and rubbing on until all the gold is sent through the sieve is to be distinctly avoided. The student must bear in mind that what he is aiming at is the exclusion of all coarse gold from the portion of ore of which he is going to take only a fraction.
The question of the smaller sampling of gold ores has been dwelt on at considerable length, as befits its importance, in order that the student may be impressed with a sense of its true meaning. Sampling is not a mystery, nor does the art lie in any subtle manner of division. It is, of course, absolutely necessary that the stuff to be sampled shall be well mixed, and the fractions taken, so that each part of the little heap shall contribute its share to the sample. Moreover, it must be remembered that tossing about is a poor sort of mixing, and that everything tending to separate the large from the small, the light from the heavy, or the soft from the hard (as happens in sifting), must be avoided, or, if unavoidable, must be remedied by subsequent mixing.
With a well-taken sample, we may rely on a great majority of our results falling within normal limits of error; but nothing can be more certain than that, in a moderately large experience we shall get, now and again, deviations much more considerable. These erratic assays can only be met by the method of working duplicates, which call attention to the fault by discordant results. Such faulty assays should be repeated in duplicate, so that we may rest the decision on three out of four determinations.
The likelihood of two very faulty assays being concordant is remote; but with very important work, as in selling parcels of ore, even this risk should be avoided, as concordance in these cases is demanded in the reports of two or more assayers. The following actual reports on a disputed assay will illustrate this: (a) 5 ozs. 1 dwt.; (b) 5 ozs. 10 dwts. 12 grains; (c) 5 ozs. 11 dwts.; (d) 5 ozs. 11 dwts. 12 grs. The mean result of several assays, unless there be some fault in the method, will be very fairly exact; and individual assays, with an uncertainty of 1 in 20, may, by repetition, have this reduced to 1 in 100 or less.
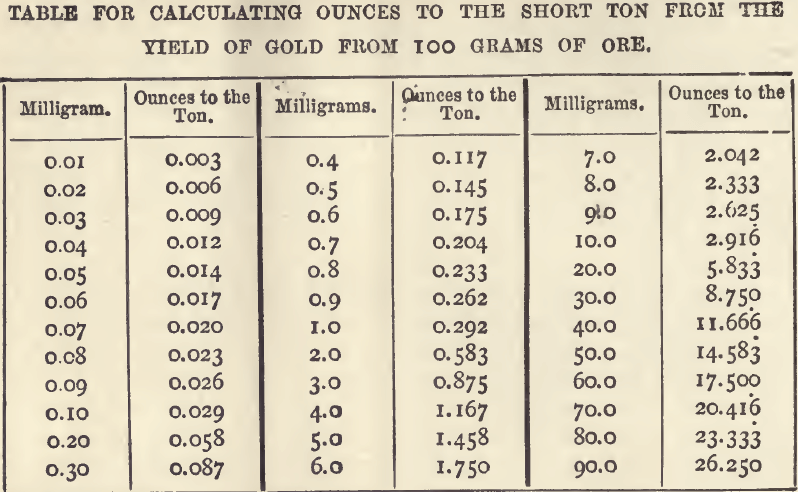
Assay Tons
Having decided on taking a larger or smaller portion, the exact quantity to be used will be either some round number of grams, such as 50 or 100, easily calculable into percentage; or it will be that known as the “ Assay Ton ” (see page 13) or some simple multiple or fraction of it, which is easily calculable into ounces. The reports, too, are at least as often made as ounces in the short ton of 2000 lbs., as on the more orthodox ton of 2240 lbs. How the short ton is equal to 29,166.6 troy ounces; and the corresponding “assay ton” is got from it by replacing ounces by milligrams. The advantage of its use is that if one assay ton of ore has been taken, the number of milligrams of gold obtained is also the number of ounces of gold in a ton of the ore, and there is absolutely no calculation. Even if half an assay ton has been taken the only calculation needed is multiplying the milligrams by two. On the other hand with a charge of two assay tons the milligrams need halving. Where weights of this kind (i.e., assay tons) are not at hand they may be easily extemporised out of buttons of tin or some suitable metal, and it is better to do this than to array out the grams and its fractions at each weighing. The sets of “assay tons,” however, are easily purchased. As stated on page 13, the assay ton for 2240 lbs. is 32.6667 grams ; and for the short ton, 29.1667 grams. If, however, the round number of grams be used and the result brought by calculation to the produce on 100 grams, the conversion to ounces to the ton may be quickly effected by the help of the table on page 107. As this table only deals with the ton of 2240 lbs., it is supplemented here by a shortened one dealing only with the produce of 100 grams and stating the result in ounces troy to the short ton of 2000 lbs.
Estimation of Small Quantities of Gold
By the Balance. In estimating minute quantities of gold there are one or two points, of importance to an assayer only in this assay, where they will often allow one to avoid the working of inconveniently large charges. One of these is known as “ weighing by the method of
vibrations.” Suppose a balance at rest in perfect equilibrium, with the pointer exactly over the middle point of the scale. Let the scale be a series of points at equal distances along a horizontal line ; then, if a small weight be placed on one pan, the pointer will deviate from its vertical position and come to rest opposite some definite part of the scale, which will depend upon the magnitude of the weight added. The law determining this position is a very simple one; the deviation as measured along the points of the scale varies directly as the weight added. For example, with an ordinarily sensitive balance, such as is used for general purposes, one milligram will move the pointer along, say, three divisions of the scale; then two milligrams will move it six divisions; half a milligram, one and a half divisions ; and so on. Of course, with a more sensitive balance the deviations will be greater. Now the point at which the needle comes to rest is also the middle point about which it vibrates when swinging. For example, if the needle swings from the third to the seventh division on the right then [ (7 + 3) ÷ 2] it will come to rest on the fifth. In working by this method the following conventions are useful: Always place the button to be weighed on the left pan of the balance, the weights on the right; count the divisions of the scale from the centre to right and left, marking the former + and the latter -; thus – 5 is the fifth division to the left. Then the position of rest is half the algebraic sum of two readings. For example, let the readings be 7 to the right and 3 to the left, then (+7 – 3) ÷ 2= + 2. The mean division is the second division to the right. If the student will place himself in front of a balance and repeat the following observations and replace the figures here given by his own, he will have no difficulty in grasping the method. First determine the bias of the balance; suppose the unloaded balance swings +1.25 and – 1; the bias then is (1.25 – 1) ÷ 2 = +.125 or one-eighth of a division to the right. Now having put on the button to be weighed let the readings be + 7.5 and +9.25, and (7.5 + 9.25) ÷ 2 =+8.375. Then the effect of the button has been to move the pointer from + .125 to + 8.375, or 8.25 divisions to the right; we should, therefore, add the weight equivalent of 8.25 divisions to the weights, whatever they may be on the right hand pan of the balance; if the divisions were to the left (- divisions) we should subtract. The value of 1 division is easily determined. Suppose the button in the example were a 1 milligram weight, then we should have found that 1 milligram = 8.25 divisions ∴ 1 division = .121 milligram. This method of working adds very considerably to the power of a balance in distinguishing small quantities.
Assay Operations
The actual work of the assay resolves itself into three operations:—(1) The fusion of the ore and concentration of the “ fine metal ” (i.e., gold and silver) in a button of lead; (2) The cupellation of the lead, whereby a button of fine metal is obtained; and (3) the “parting” of the gold which separates it from the accompanying silver. The following description takes the order as here given, but the student, in learning the method, should first practise cupellation if he has not already done so; next he should practise the separation of gold from silver, taking known weights of fine gold (p. 63), varying from .5 or .3 gram down to quite minute quantities, and not resting satisfied until a sensitive balance can barely distinguish between the weights of gold taken and found. It may be noted here that if he has not a flatting mill at his disposal, then for large buttons it is better to make an alloy with eight or nine parts of silver to one of gold, and attack it with acid without previous flattening, rather than accept the risk and labour of beating out a less easily attacked alloy to the necessary thinness with a hammer. It is only after a sense of security in gold parting has been acquired, that the attack of an ore can be profitably accomplished, and even then simple and easy ores should be first taken, passing on to others more difficult, either because of a more complex mineral composition or a difficulty in sampling.
Concentration of the fine Metal in Lead
The best flux for quartz, which makes up the earthy matter of most gold ores, is soda, and this is best added as carbonate or bicarbonate. By theory, 50 grams of quartz will require 88.5 grams of the carbonate, or 140 grams of the bicarbonate, to form sodium silicate, which is a glassy, easily-fusible substance, making a good slag. If the bicarbonate is used, and heat is applied gradually, steam and carbonic acid are given off at a comparatively low temperature, and the carbonate is loft; at a higher temperature (about 800° C., or a cherry-red heat) the carbonate fuses attacking the quartz, and giving off more carbonic acid; as the heat increases, and the attack on the quartz (which of itself is infusible) becomes complete, the whole mass settles down to a liquid sodium silicate, which is sufficiently fluid to allow the gold and lead to settle to the bottom. The fluid slag does to a certain extent dissolve some of the crucible, but not seriously. In a perfect working of this experiment, the first evolution of gases (steam and carbonic acid) should be gentle, so as to run no risk of its blowing the fine powder out of the crucible; and the heat at which the second evolution of carbonic acid is produced should be maintained until the reaction is completed, so that there may be little or no formation of gas in the fused mass to cause an effervescence which may force some of the charge over the edges of the crucible. Of course, in practice the ideal fusion is not attained, but there is no difficulty in approaching it closely enough to prevent the charge at any time rising above the level it reached at first in the crucible, and this should be accomplished. It is usual with quartzose ores to rely mainly on the action of carbonate of soda, but not entirely. Litharge is also used; it forms, on fusion with quartz, a silicate of lead, which is a yellow glass, easily fusible, and more fluid in the furnace than silicate of soda is. By theory, 50 grams of quartz would require 186 grams of litharge. The reaction takes place without evolution of gas, and in its working the only point is to so regulate the heat that the litharge shall not fuse and drain under the unattacked quartz, leaving it as a pasty mass on the surface. Now, if in making up a charge for 50 grams of ore, we took 100 grams of bicarbonate of soda (equivalent to about 63 grams of the carbonate), this being five-sevenths of 140 grams (which by itself would be sufficient), leaves two-sevenths of the quartz to be fluxed by other reagents: two-sevenths of 186 grams (say 52 grams) of litharge would serve for this purpose. But if we used 10 grams of borax, which has a fluxing action about equal to that of the litharge, then 40 grams of the latter, or (making an allowance for the quartz being not quite pure) say 35 grams, will suffice. The fluxes, then, for the 50 grams of ore would be: bicarbonate of soda 100 grams, litharge 35 grams, and borax 10 grams; we could decrease any of these, and proportionately increase either or both of the others, and still rely on getting a fusible slag, which is the whole of the function of a flux, considered simply as a flux. It should be remembered, however, that the slag is a bi-silicate or acid slag, and that its acid character is increased by increasing the proportion of borax.
But in addition to the fluxes there is required about 30 or 40 grams of lead to collect the silver and gold. This is best added as litharge (say 40 grams) and flour (4 grams), or charcoal powder (2 grams). See pages 93 and 94. The full charge, then, would be:

These should be mixed, placed in a suitable crucible (a G Battersea, round, will do), and heated, at first at a red heat, but finally much hotter, so as to get a fluid and clean slag. When the charge has been in tranquil fusion for some little time, take it out and pour it into an iron mould. When cold, detach the button of lead. The slag should be glassy, all through alike, and easily separable from the metal. With ordinary ores, this slag may be considered as free from gold. In an experiment in which 90 milligrams of gold were added, the full amount was obtained from the lead produced by the first fusion. But in certain cases, more especially where large amounts of metallic oxides are present, the slag is not so clean, and with these the slag should be powdered, mixed with 40 grams of litharge and 4 of flour, and melted again; it is an advantage to add a small prill of say 2 or 3 milligrams of silver to the charge, as it insures a visible product in the cupellation. Indeed, this last precaution is a good one to be taken wherever there is reason to expect very small buttons. It has the further advantage, that, if the quantity of silver necessary for inquartation is known, the right quantity may be added here, so as to save a subsequent operation.
Ores containing Oxides of Iron
Of the metallic oxides likely to be present in a slag, oxide of iron is the most important. Gold is occasionally found in a matrix of this substance, and in the assay of “concentrates” largely made up of pyrites, this oxide will be formed in the preliminary calcination. Now, the lower oxide of iron (ferrous oxide, FeO) is easy to deal with; fused borax will dissolve about its own weight of it, and a silicate of soda (such as makes up the bulk of a slag in a gold assay) will take up at least half as much. But the higher oxide (ferric oxide, Fe2O3) is more refractory; even 6 parts of borax yields a poor product, and slags with any considerable percentage of it are not satisfactory. A student attempting to recover gold from some haematite (in which there was about half an ounce of the metal), found in the slag nearly a gram of gold, although in the first fusion the slag appeared perfectly fluid. There is, however, no difficulty in getting good slags, even with large quantities of iron. For example, with 50 grams of ferric oxide, 10 of quartz, 30 of borax, 30 of soda, 50 of litharge, and 7 of flour, the result was quite satisfactory. So, too, was 25 of quartz, 50 of soda, 50 of litharge, and 7 of flour. It is well, however, in such cases to have an ample proportion of flux and to aim at a larger button of lead than usual by increasing the proportion of flour or charcoal (see also page 91). A charge used on the Randt for roasted “concentrates ” (which we may roughly speak of as quartz and ferric oxide), is one assay ton (about 30 grams) each of ore, soda, and borax, and one and a half assay ton of litharge and 2 grams of charcoal. Whilst, for the same material, from which most of the gold has been extracted by “ chloridising,” 2 5 tons each of ore, borax, and soda, 4 of litharge, and 4 grams of charcoal are needed. This quantity requires a large crucible (I Battersea, round). In this the proportion of silicate of soda and borax counted together is to the oxide of iron as 4 to 1, on the supposition that the quartz and oxide of iron of the ore are in about equal quantities; but, in the larger charge especially, much oxide of lead would also remain as a flux.
Ores containing Sulphides
In assaying ores containing a large proportion of pyrites or mispickel, or both, the best plan is to take a portion and calcine so as to convert it into a product of the kind just considered. The weighed portion of ore should be placed in a clean crucible and be heated to incipient redness: with pyrites the first effect is to drive off about half the sulphur as vapour which burns as flame over the ore. At this stage care should be taken that there is no great increase of temperature, otherwise there may be more or less fusion, which would spoil the operation. When the sulphur flame ceases the solid sulphide of iron burns with visible incandescence and the charge should now be stirred with a flattened iron rod so as to expose fresh portions to the air. The top of the furnace must be open, so that air may have free access to the crucible. When stirring is no longer followed by visible burning the heat may be raised to full redness. The crucible is then lifted out (the stirrer still resting in it) and if the charge gives off no odour of burning sulphur it is shaken out into an iron mortar and mixed with the fluxes, taking care to clean the stirrer in the mixture. The charge is then replaced in the crucible in which the roasting was done and fused in the furnace. The resulting button of lead is cupelled for fine metal. Ores rich in sulphides requiring this treatment are frequently “concentrates.” For their assay take 1 assay ton (30 grams), calcine and mix with an equal weight of soda and of borax (30 grams each), and half as much again of litharge (1.5 tons or 45 grams), and with 2 grams of charcoal or 5 grams of flour.
Where the sulphides are present in smaller proportion (10 per cent, or less), they may be taken as serving the purpose of flour or charcoal (see page 95); the sulphur and iron are oxidised at the expense of the litharge with a consequent separation of lead as metal. If the proportion of sulphides is not sufficient to give a large enough button of lead, some charcoal or flour should be added. On the other hand, if they are in small excess and give a button of lead somewhat sulphury, i.e., hard and brittle, it may be remedied by the judicious addition of nitre; this last reagent, however, should not be used in large quantity. A plan much used to prevent sulphury buttons is to insert an iron rod or a nail in the charge in the crucible; the iron takes the sulphur forming sulphide of iron which in moderate quantity does not form a separate layer of matte but dissolves in the slag. A slag formed of 50 grams of quartz, 100 soda, and some borax, may take up in this way some 10 or 12 grams of sulphide of iron. If, however, an ore gives a layer of matte or speise, it is best to repeat the assay by the method of calcining before fusion.
Cyanide Charges, etc.—In assaying the “ tailings ” which are to be treated in a cyaniding plant the following charge is used:

The sand is assayed without any further crushing and the assay is made in duplicate.
The residues after treatment with cyanide, differing from the tailings merely in being poorer in gold because of the extraction by the solution of cyanide, are run down with the same fluxes in the same relative proportions. But four charges of 2.5 assay tons (say 75 grams) are worked, and two of the resulting buttons are scorified together and then cupelled, etc., so as to give duplicate assays on charges of 5 assay tons. This is one of the cases in which it is desirable to add a small portion of silver before cupelling.
In assaying the “cyanide liquors ” for gold, 2 assay tons of the liquor are measured out (58.3 c.c. for the ton of 2000 lbs., 65.3 c for the other) and are evaporated to dryness in a lead dish weighing about 35 grams. Such a dish is easily extemporised out of a piece of lead foil, if the ordinary vessel is not at hand; but care must be taken that the lead is free from gold. The dish with the dried residue is then scorified and the resulting button of lead is cupelled.
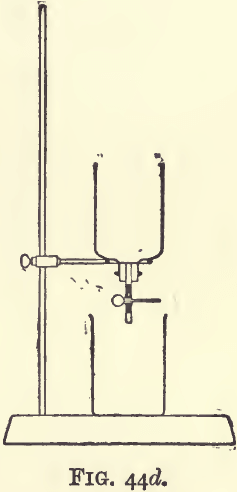
In some cases the fusion of the ore may be replaced by a treatment with solution of cyanide of potassium and the gold recovered from the solution in the way just described. For this purpose the ore should be in not too fine powder, otherwise there will be great difficulty in filtering; a sand which will pass a 30 sieve and having no large proportion of very fine stuff will do. Not less than 200 grams should be taken; and as an extraction apparatus a bell jar capable of holding half as much again may be used. Such a jar may be extemporised by cutting off the bottom of a bottle by leading a crack around it with a red hot poker; or a lamp chimney will serve the purpose. The smaller mouth of the jar is closed by a perforated cork provided with a clipped tube after the manner of a burette (see fig. 44d). In the jar, just over the cork, put a plug of loose asbestos or glass wool, or a piece of sponge to act as a filter; a layer of broken glass, coarse at the bottom and fine at the top, will serve the same purpose. On this, place the charge of ore to be extracted. Prepare a solution of cyanide of potassium in water, with 5 or 10 grams of the salt to the litre. It may be that the whole point of the assay depends on the solution being of a definite strength; as, for example, where the relative efficiency of solutions of different strengths is being determined, when it will be best to estimate the quantity of cyanide of potassium in the dilute solution by the method given at the end of this article (page 160). Pour the cyanide solution on to the ore, letting the first portions to come through run into the beaker, but as soon as the ore is thoroughly wetted close the clip and allow to stand for several hours. Then, opening the clip, run through more cyanide solution and then water, so as to wash the gold-carrying liquor thoroughly into the beaker. It is no matter if the liquor is a little bit turbid; transfer it to a lead dish, evaporate, scorify, and cupel in the usual fashion,
The assay of gold-zinc slimes, which is the precipitate formed by zinc acting on cyanide solutions of gold, may be made by wrapping 2 or 3 grams in 40 grams of sheet lead and scorifying, cupelling, &c. The amount of impurity in the stuff varies greatly; it is usually calcined and mixed thoroughly with soda 40 per cent., borax 30 per cent., and sand 10 per cent., and melted in graphite pots. The buttons of bullion obtained are afterwards remelted with borax and run into bars, the fineness of which varies from 600 to 830 thousandths. The bars are sampled by chipping off diagonally opposite corners: or better, by drilling, the drillings being freed from pieces of steel with the help of a magnet.
