Gasometric methods are not much used by assayers, and, therefore, those students who wish to study them more fully than the limits of this work will permit, are recommended to consult Winkler and Lunge’s text-book on the subject. The methods are without doubt capable of a more extended application. In measuring liquids, ordinary variations of temperature have but little effect, and variations of atmospheric pressure have none at all, whereas with gases it is different. Thus, 100 c.c. of an ordinary aqueous solution would, if heated from 10° C. to 20° C., expand to about 100.15 c. c. 100 c. c. of a gas similarly warmed would expand to about 103.5 c.c., and a fall of an inch in the barometer would have a very similar effect. And in measuring gases we have not only to take into account variations in volume due to changes in temperature and atmospheric pressure, but also that which is observed when a gas is measured wet and dry. Water gives off vapour at all temperatures, but the amount of vapour is larger as the temperature increases.
By ignoring these considerations, errors of 3 or 4 per cent, are easily made; but, fortunately, the corrections are simple, and it is easy to construct a piece of apparatus by means of which they may be reduced to a simple calculation by the rule of three.
The volume of a gas is, in practice, usually reduced to that which it would be at a temperature of o° C., when the column of mercury in the barometer is 760 mm. high. But, although convenient, this practice is not always necessary. The only thing required is some way of checking the variations in volume, and of calculating what the corrected volume would be under certain fixed conditions.
Suppose that at the time a series of standardisings is being made, 100 c.c. of air were confined in a graduated tube over moist mercury. These 100 c.c. would vary in volume from day to day, but it would always be true of them that they would measure 100 c.c. under the same conditions as those under which the standardisings were made. If, then, in making an actual assay, 35.4 c.c. of gas were obtained, and the air in the tube measured 105 c.c., we should be justified in saying, that if the conditions had been those of the standardising, the 105 c.c. would have measured 100 c.c., and the 35.4 c.c. would have been 33.7 ; for 105 : 100 :: 35.4 : 33.7. The rule for using such a piece of apparatus for correcting volumes is :—Multiply the c.c. of gas obtained by 100, and divide by the number of c.c. of air in the apparatus.
If it is desired to calculate the volumes under standard conditions (that is, the gas dry, at o° C. and 760 mm. barometric pressure) the calculations are easily performed, but the temperature and pressure must be known.
Correction for Moisture.—The “ vapour tension ” of water has been accurately determined for various temperatures, and it may be looked upon as counteracting the barometric pressure. For example, at 15° C. the vapour tension equals 12.7 millimetres of mercury; if the barometer stood at 750 mm., the correction for moisture would be made by subtracting 12.7 from 750, and taking 737.3 mm. to be the true barometric pressure.
The vapour tensions for temperatures from o° C. to 20° C. are as follows :—

The correction for pressure is:—Multiply the volume by the actual pressure and divide by 760.
The correction for temperature :—Multiply the volume by 273 and divide by the temperature (in degrees Centigrade) added to 273.
For all three corrections the following rules hold good. To reduce to 0° C. and 760 mm. dry.
Corrected Volume = Volume x 0.3592 x (Pressure – Tension)/Temperature + 273
To find the volume, which a given volume under standard conditions would assume, if those conditions are altered.
Resulting Volume = Volume x 2.784 x Temperature + 273/Pressure – Tension
As an example, we will suppose that it is desired to enclose in the apparatus referred to on p. 45, a volume of air, which, when dry (at o° C. and 760 mm.), shall measure 100 c.c., whilst the actual temperature is 15° C., and the pressure 750 mm.
The second formula is the one to be used, and we get 108.7 c.c.

Of this type of analysis only one example will for the present be given, as the subject will again be considered in Part III.—“The Analysis of Furnace Gases.”
Apparatus, Reagents.—The special piece of apparatus termed the nitro¬meter is shown in fig. 69, and consists of two vertical glass tubes a and b, connected at the foot by a length of stout-walled rubber tubing c, and attached by clamps to a suitable stand. The tube b is plain, but the tube a is graduated from the top downwards, usually in 50 c.cs. divided in tenths. The top of this tube is contracted and terminated in a tap (Greiner and Friedrich’s patent), surmounted by a funnel d and a capillary tube e. By this tap the tube may be connected to either the funnel or capillary, or may be disconnected from both.
Various forms of nitrometer are in use (see Sutton), but for the present the student may employ the form just described.
For analysis the student may take a sample of potassium nitrate and estimate the percentage of NO3 present. For this purpose quicksilver will be necessary for the measuring liquid, and in reading its volume the student may read the top of the meniscus.
Method, Reactions.—When strong H2SO4 is added to a solution of KNO3 the following reaction occurs,
KNO3 + H2SO4= HNO3 + KHSO4
the acid sulphate being formed, and in the presence of mercury the nitrogen is liberated as nitric oxide, NO.
2KNO3 + 3Hg2SO4 + 4H2SO4 = K2SO4 + 6HgSO4 + 2NO + 4H2O.
From the measured volume of NO the percentage of NO3 present may be calculated.
101 gms. KNO3 contain 30 gms. NO, or 1 gm. KNO3 contains 30/101 = .297 gm. NO.
But 1 litre NO at normal pressure and temperature weighs .0896 x 16 + 14/2 = 1.344 gms., therefore the volume of .297 gm. NO at normal temperature and pressure will be 1000 x .297/1.344 = .221 c.cs. That is, 1 gram of pure KNO3 will produce 221 c.cs. of NO at normal temperature and pressure. Then 1 c.c. of NO under these conditions will correspond to 1/21 = .00452 gm. KNO3 or .00452 x 62/101 = .00277 gm. NO3.
Measurement of Gases.—To obtain a correct reading of the volume of a gas, the following factors have to be taken into account:—
- The Temperature of the Gas.
- The Pressure of the Gas.
- The Aqueous Vapour present.
1. The Temperature of the Gas.—As the volume of a gas varies directly as the absolute temperature T (= centigrade temperature + 273) when the pressure is constant, then, if the temperature at which the volume of the gas is read is t° C., and V = the volume at t° C., then the volume V0 at 0° C. is obtained thus,—
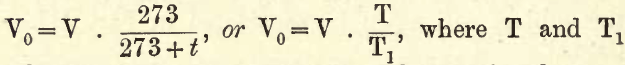
are the absolute temperatures at the centigrade temperatures 0° and t° respectively.

2. The Pressure of the Gas.—When the temperature of a gas is constant the volume varies inversely as the pressure. This pressure, being in the analysis considered as that due to the atmosphere, is taken as the height of the barometer in millimetres, the standard pressure being taken at 760 mm. Then if V0 be the volume at 760 mm. and V be the volume read in the analysis at a barometric pressure P1,
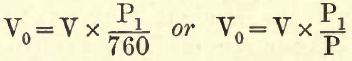
where P1 = pressure in analysis and P = standard pressure.
Combining 1. and 2. we get
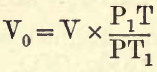
For example, find the volume at standard temperature and pressure of 20 c.cs. at 17° C. and 770 mm. barometric pressure.
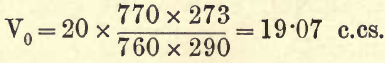
3. The Aqueous Vapour present.—If any aqueous vapour (moisture or humidity) be present in the gas measured it exerts a pressure against the pressure of the atmosphere (barometric pressure), therefore the volume of a gas is increased if aqueous vapour be present. For the student’s purpose he may take the pressure or tension of aqueous vapour from the following table; for very accurate work, however, he should refer to the tables given in physical text-books.

Thus, for example, if a gas contain aqueous vapour and be at a temperature of 18° C., this aqueous vapour will exert a pressure of 15.4 mm. against the barometric pressure; therefore, in making the necessary calculation, this quantity must be subtracted from the barometric reading, and the correction formula now becomes—

where P2= the pressure or tension of the aqueous vapour. Thus, in the example just given,

The Analysis.—Raise the tube b and into it pour quicksilver until it just reaches the glass tap in a and fills the bottom two inches of b. This condition is obtained by raising or lowering the tube b as may be required. Close the tap and clamp b. Weigh out .1 gm. KNO3. Transfer to the funnel. Add 2 to 4 c.cs. of water, and when dissolved open the tap, connecting the funnel to a, and gently unclamp and lower b till the liquid has passed into a. Rinse the funnel with about 1 c.c. of distilled water from a wash bottle with a fine jet. Again lower b till the wash passes into a. Then rinse the funnel with 3 c.cs. 36E. H2SO4, running it down a glass rod against the sides of the funnel. Again lower b till the acid passes into a. Quickly add another wash of 3 c.cs. 36E. H2SO4. Close the tap when the wash is transferred to a. If any air has been enclosed during these operations it should be removed by raising the tube b slightly and gently opening the tap, and when the air has escaped the tap is closed.
Unclamp a; incline it in both hands almost horizontally, and with a quick motion bring it back to the vertical. Repeat this process for two or three minutes, so that the mercury and the acid are well mixed. Now adjust the tubes in the clamps so that the mercury in a is approximately at the same level as that in b. Allow to stand till the temperature coincides with that of the room. Now carefully adjust the tube b so that the mercury in it is higher than that in a by 1 mm. for every 6.5 mm. of solution in a. This makes the necessary allowance for the short column of liquid in a. Read the volume of gas in a (call this V).
Open the tap. The level of the mercury should not alter. Raise b so that the liquid passes into funnel. Take the temperature of the liquid (call this t° C.) and read the height of the barometer (call this P1).
From the table obtain (by interpolation if necessary) the vapour pressure corresponding to the temperature t° C. Then by the formula—
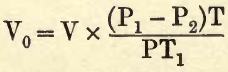
calculate the volume of the gas at normal temperature and pressure.
Multiply this volume by the value of 1 c.c. of NO in terms of NO3 (1 c.c. = .00277 gm. NO3) and the quantity of NO3 present is obtained. The percentage is calculated as usual.
Note.—When estimating the NO3 in KNO3 or NaNO3 it is more convenient to use the modified (Lunge’s) form of nitrometer of large capacity. Larger quantities of nitrate may then be taken for analysis.
Further information regarding the use of the capillary tube will be found in Sutton’s Volumetric Analysis.
In Part III. the Hempel burette will be described, and the student should note that with it, as the volumes read are relative and the conditions nearly uniform, it is not necessary for general work to make the temperature and other corrections just described. In the time taken for the analysis the fluctuations in these are, with care, but slight.
