Table of Contents
Selective beneficiation of fine particles depends heavily upon the flotation separation process. Conventional froth flotation for many ore systems is very effective for particles between 300 and 20 µm in size, but the flotation efficiency commonly drops off as the particle size decreases below 20 µm. Flotation kinetics has been used by Sutherland (1955) and subsequent researchers to explain this inefficiency. The rate of flotation of a particle by a bubble was expressed by Kelley (1982) as
K = Pc · Pa · Pf · Pr…………………………………………………………………………………(1)
i.e., as the product of the probability of collision (Pc) between the particle and bubble, the probability of attachment (Pa) between the bubble and particle, the probability of the bubble with particle attached entering the froth (Pf), and the probability of the bubble and particle remaining attached throughout the flotation process (Pr). For the most part, the probability of attachment depends upon the surface characteristics of the mineral and the degree of collector absorption on the mineral surface. Philippoff (1952) showed that the contact time or induction time for effective attachment of the hydrophobic particle to the bubble decreased as the particle size decreased. This did not account for the decline in flotation efficiency for fine-sized particles, so that attachment probability was not the explanation for the reduced flotation efficiency of fine particles. For the Pf and Pr factors, the small mass of fine particles tends to enhance their ability to rise to the froth with the attached bubble and remain attached throughout the flotation process.
The probability of collision depends upon the size of the particles and bubble and the hydrodynamics of the flotation pulp. This probability is directly related to the number of collisions per unit time and unit volume. Bischofberger and Schubert (1978) presented the following formula for the number of collisions in a flotation system:
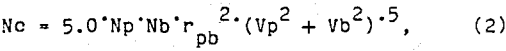
where Np is the number of particles,
Nb is the number of bubbles,
rpb is the sum of particle and bubble radii, and
Vp² and Vb² are the mean squares of the effective relative velocity between the particle and bubble.
Nonaka et al. (1982) proposed a turbulent diffusion collision model for particle behavior in flotation:
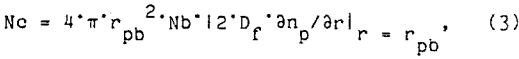
where Df, is the diffusion coefficient of the fluid and ∂n/∂r is the concentration of particles at the collision radius of rp + rb. Using Kolmogoroff’s theory of isotropic turbulence, the velocities of the bubbles and particles become a function of the dissipation energy within the flotation cell. For Bischofberger and Schubert’s equation,
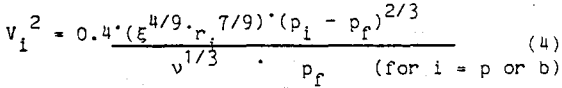
where ξ is the dissipation energy per unit mass and time,
v is the kinematic viscosity,
Pf is the fluid density, and
Pi is the density of the particle (p) or bubble (b).
The dissipation energy per unit mass and time is determined by the flotation cell design and the impeller speed. Substituting the bubble and particle velocities obtained from equation 4 into equation 2, the number of collisions can be calculated and the probability of collision can be determined.
For Nonaka et al., the relative diffusion coefficient of the bubble and particles was equated to the diffusion coefficient of the fluid. Using Kolmogoroff’s isotropic turbulence theory,
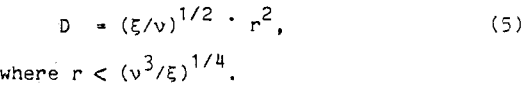
Substituting equation 5 into equation 3, the probability of collision can be reduced to
Pc = K·ξ-¼·Nb……………………………………………………………………………………(6)
where K is the proportionality constant determined by the properties of the flotation pulp.
From these equations, fine particles are shown to have a lower relative velocity and thus a lower collision probability, which helps to explain the flotation inefficiency of conventional fine-particle flotation. However, the equations also suggest ways to improve the collision probability. Small bubbles for flotation have been proposed by many researchers. While small bubbles have lower relative velocities, their numbers increase substantially at the same airflow rate, which brings an increase in the particle collision probability. Improved flotation of fine particles should be obtained with small bubbles. Another way to improve fine-particle flotation is to increase the turbulent dissipation energy within the flotation cell and thereby increase the collision probability of fine particles. While this should improve the collision probability, it may lower the probability of the particle remaining attached (Pr) by increasing the turbulence energy level of the fluid. As part of the Bureau of Mines research program to maximize the recovery of mineral values during the processing of mined ore, the Bureau conducted research on the importance of bubble-particle collisions to the flotation response of fine particles. Flotation studies were conducted on a chalcopyrite ore to compare the actual flotation response with the predicted response of the flotation models developed by other researchers. Conventional laboratory flotation was used along with several techniques for fine-bubble flotation.
Sample Description
An ore sample was obtained from the Cyprus Bagdad porphyry copper mine in Arizona. A partial chemical analysis of the ore sample is shown in table 1. The major sulfide mineral was chalcopyrite with smaller amounts of pyrite. The gangue was mostly plagioclase feldspar with small amounts of biotite and magnetite. The chalcopyrite was widely disseminated throughout the ore pieces, and the liberation size was around 210 µm.
Experimental Procedure and Equipment
For each flotation test, the ore sample was ground with clear saturated lime water for 1 h in a laboratory rod mill at 65 pct solids and screened at 38 µm size. The plus 38-µm fraction was reground for another hour. The ore sample was overground to obtain enough minus 20-µm particles for this research. The size distribution and analysis are shown in table 2.
The ground ore pulp was thickened to 50 pct solids, followed by flotation conditioning in a high-speed blender (1,700 r/min) to ensure complete coverage with the flotation collector. Clear saturated lime water was used to keep the pH at 12.4 to 12.5. Potassium amyl xanthate at a dosage of 0.025 g/kg was used for the chalcopyrite collector. After conditioning for 5 min, the sample was ready for flotation. The slurry was placed in a conventional 500-g Denver DR flotation cell. The pulp was diluted to 25 pct solids with clear saturated lime water, and Dowfroth 100 frother was added to raise the frother concentration to 25 ppm (0.075 g/kg). The sample was floated for 5 min at 1,000 r/min with 1.5 L/min of air. Saturated lime water was used to maintain the pH and the froth height. After the 5 min rougher flotation, the froth product was cleaned in a 250-g Denver DR flotation cell at 1,000 r/min and 1.5 L/min of air for 3 min. Regardless of the rougher flotation technique, all of the cleaner flotations were conducted by the same procedure. Only one cleaner float was used because after the first cleaner float the amount of concentrate was too small to allow additional meaningful cleaner floats at the laboratory scale. The final concentrate, cleaner tailings, and rougher tailings were dried and analyzed for copper. The above procedure was called “conventional” flotation and formed the baseline characteristics for comparison with the alternative flotation methods. The second type of flotation, defined as high-speed conventional flotation, used the same procedure as the conventional flotation method except the impeller speed was increased to 2,100 r/min for the rougher flotation stage.
Fine-bubble flotation was conducted in a modified 500-g MS flotation cell. A 6-cm-diam, 2-cm-thick disk was used to replace the flotation impeller. Sebba (1985) showed that at high rotation speed, the spinning disk sheared air in the pulp and formed fine-sized bubbles. The cell was tested at 2,800 r/min, 1,300 r/min, and 7,000 r/min. The laboratory procedure, reagent levels, and airflow rate were identical to those from the conventional flotation method. The spinning disk flotation cell was only used for the rougher flotation stage.
Tailings Analysis
Before drying, a portion of the flotation tailings was split out for size and chemical analysis. Sedimentation based upon Stoke’s Law was used to obtain sized samples for chemical analysis. The samples were diluted to about 3 pct solids with tap water. Tetrasodiun pyrophosphate (TSPP) was used to disperse the particles and allow free settling. Separations were made at 20, 10, 5, and 2 µm. The samples were settled and siphoned three times at each size fraction to ensure a clean and sharp size separation. After each size separation, the dispersed size fraction was flocculated and dried for chemical analysis. A Microtrac particle size analyzer was used to measure the size distribution of the tailings sample and to confirm the size range of each sedimentation fraction, acting as quality control over the sedimentation separation process.
Bubble Size Measurements
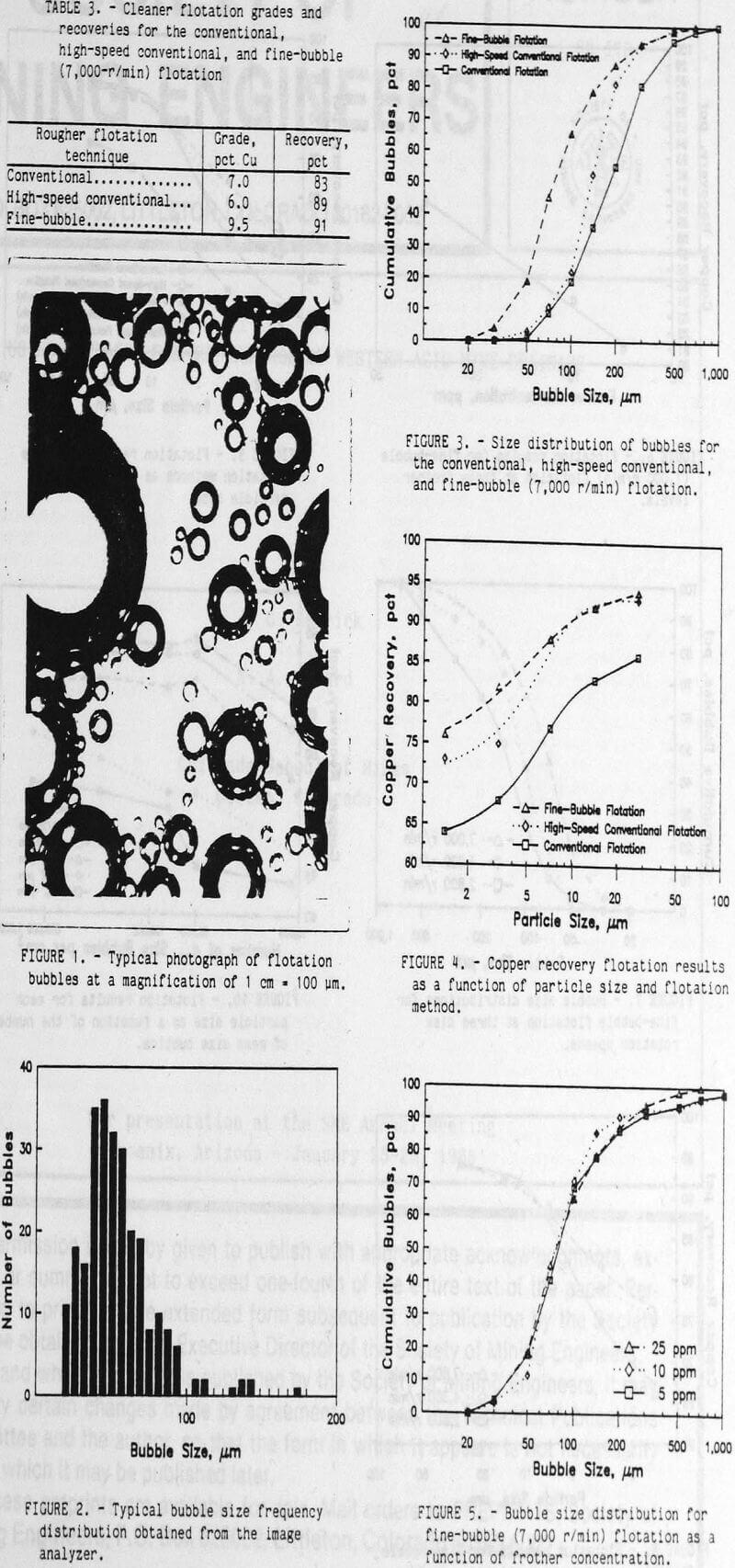
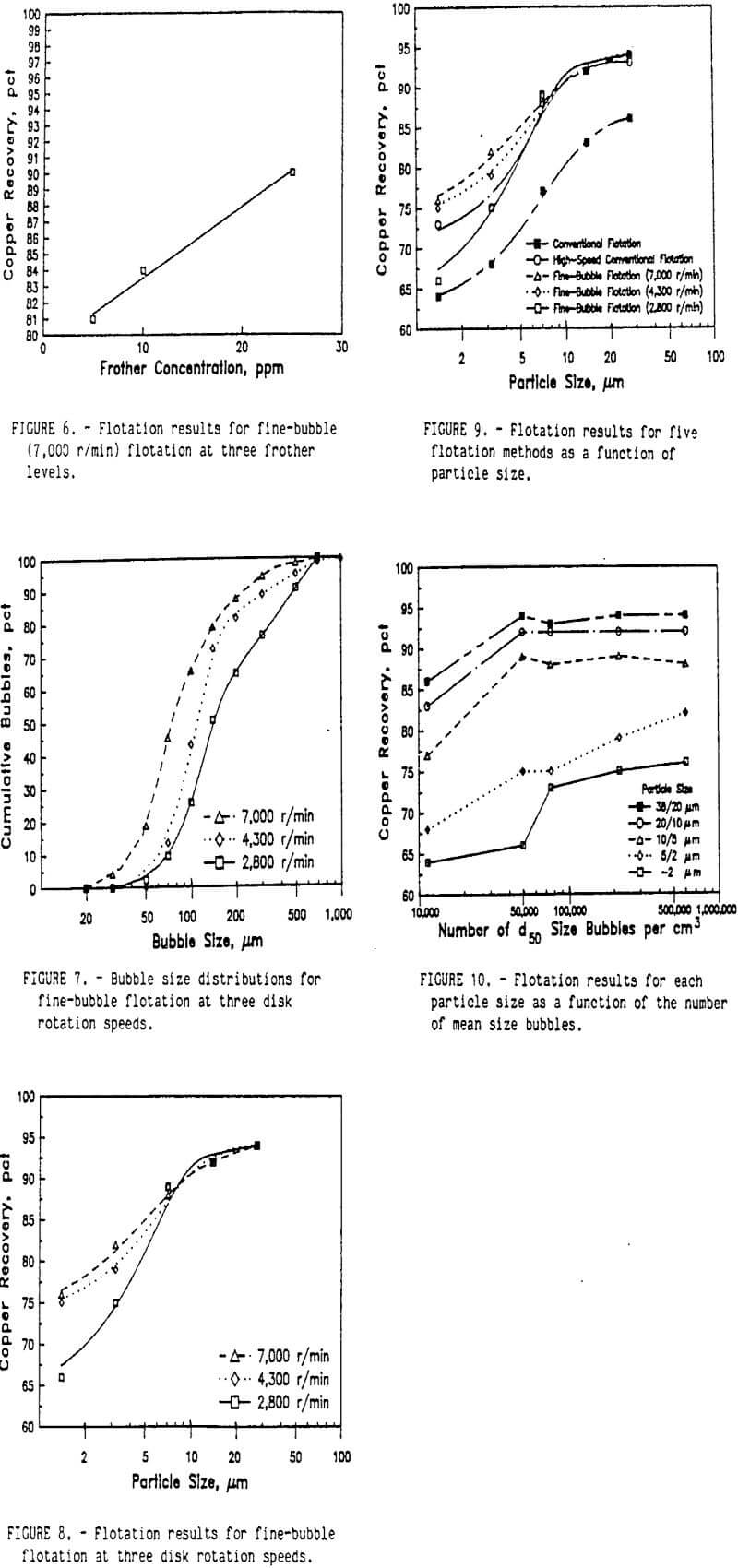
The size distribution of the flotation bubbles was obtained by the following method. A flotation test was conducted without the ore sample, but included the water, reagents, and air. A sample of the bubble slurry was continuously drawn through a small tube to an observation cell under a microscope. The observation cell was two microscope slides separated by 1 mm. The sides and ends of these slides were sealed to prevent leakage of the bubble slurry. A peristaltic pump was used to draw the bubble slurry through the microscope observation stage and return it to the flotation cell. Periodically the pump was stopped and a photograph of the bubble slurry was quickly made through the microscope. A typical photograph of the bubbles is shown in figure 1. These bubble photographs were evaluated with an image analyzer to determine the bubble sizes and the frequency distribution of each size bubble. A typical frequency distribution for several of these photographs is shown figure 2. During each test, the air content of the bubble slurry was measured by pumping the slurry to a graduated cylinder. After all the bubbles had burst, the volume of water was measured and the air content of the bubble slurry was calculated.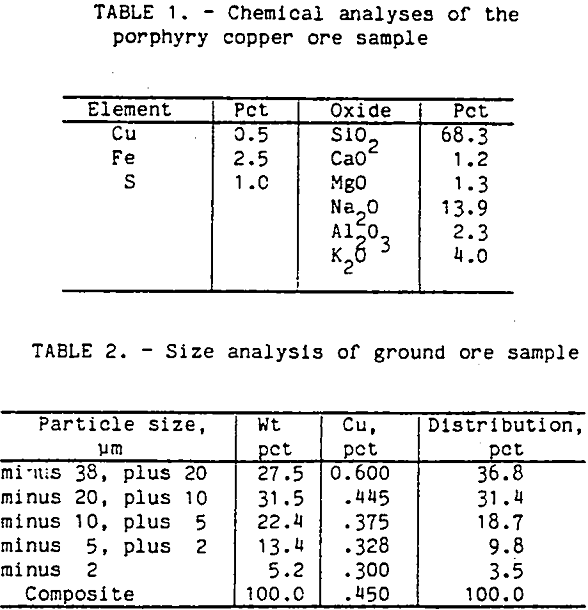
Factorial Experimental Design
The improved recovery of the fine chalcopyrite with fine bubbles can effectively be evaluated in a factorial experimental design, as reported by Davies (1956), to clearly sort out the experimental error from the effects of the alternative treatment methods. A two-factor factorial design was used for most of the research experiments. The treatment method was one factor, and the size fraction of the ore was the second factor. These two factors were blocked with two to four replications. From this design, analysis of variance for the experiments was performed, and the significance of each treatment method was rigorously determined at a 95-pct confidence level as shown by Scheffi (1959).
Results and Discussion
The measured bubble size distribution of conventional (1,000 r/min), high-speed (2,400 r/min) conventional, and fine-bubble (7,000 r/min) flotation is shown in figure 3. The conventional flotation method produced the largest bubbles and had a d50 of 128 µm. This was considerably smaller than the d50 bubble size of 300 to 600 µm for conventional flotation reported by Sutherland (1955) and Kelley (1982). However, this fine-size distribution of bubbles will be adequate for comparing the smaller size distributions of flotation bubbles generated by the high-speed conventional and fine-bubble flotation techniques. Both the high-speed (2,400 r/min) and the fine-bubble (7,000 r/min) flotation techniques produced smaller bubbles than the conventional method. The d50’s for the high-speed conventional and fine-bubble techniques were 97 and 51 µm, respectively. Even though the airflow remained constant, the fine-bubble (40 pct air by volume) and the high-speed conventional (29 pct air by volume) flotation techniques suspended more air throughout the pulp than the conventional flotation (10 pct air by volume) method. The increased air suspension was caused by the production of smaller bubbles that slowly rise out of the pulp and by the increased agitation in the pulp at the higher impeller speeds. This agitation kept the bubbles suspended and delayed their movement into the froth. According to Bennett (1962), the increased agitation with the high-speed conventional flotation was expected because the same impeller was used in both conventional and high-speed conventional flotation. However, the spinning disk impeller did not have the small baffles located on the peripheral of the conventional Denver flotation impeller. At 7,000 r/min the agitation from the spinning disk appeared to be higher than the conventional flotation agitation, but lower than the high-speed conventional agitation.
The rougher flotation results for the conventional, high-speed conventional, and fine-bubble flotation tests are shown in figure 4. Analysis of variance of the factorial block design experiment indicated that the effects of the flotation method and the size fraction were significant at a 95-pct confidence level. The recovery of fine chalcopyrite decreased as the particle size decreased. Both high-speed conventional and fine-bubble flotation recovered more chalcopyrite for each size fraction than conventional flotation. For chalcopyrite particles larger than 5 µm, both high-speed conventional and fine-bubble flotation recovered the same amount of chalcopyrite in each size fraction. However, below 5-µm particle size fine-bubble flotation recovered the most chalcopyrite.
Improved recovery at the expense of concentrate grade would not be desirable in most cases. Table 3 shows the grades of the single cleaner flotation. The fine-bubble flotation concentrate was higher grade than the conventional and high-speed conventional flotation concentrates. Due to the small amount of concentrate obtained, these cleaner flotation steps were conducted at low percent solids and may not be typical for a commercial operation. Additional flotation cleaning would be required to obtain a commercial-grade concentrate, but the small quantity of concentrate obtained in these laboratory-scale tests precluded any additional meaningful cleaner flotation tests. However, these results do indicate that the improved flotation recovery was obtained with fine-bubble flotation and without sacrificing flotation selectivity. Both flotation models predicted that the smaller bubble size at the same airflow would produce more bubbles and increase the rate of flotation. Also, increased agitation would increase the relative velocities of the particles and bubbles and increase the rate of flotation. Both high-speed conventional and fine-bubble flotation showed improved flotation rates for all sizes of chalcopyrite.
To separate the effects of small bubbles from the effects of increased agitation, fine-bubble flotation tests were conducted at the same disk rotation speed (7,000 r/min), but with different amounts of fine bubbles. As shown in figure 5, varying the frother concentration from 5 to 25 ppm had little effect upon the bubble size distribution. However, the air suspension percentage was 20, 30, and 40 pct for fine-bubble flotation with 5, 10, and 25 ppm frother. The flotation tests results at all three frother concentrations are shown in figure 6. Although size analyses were not obtained with these tests, the overall chalcopyrite recovery was almost linear with respect to the air suspension percentages. As the air suspension percentage increased, the number of bubbles increased proportionally and the flotation rate also increased. Both flotation models (equations 2 and 5) accurately predicted the increased flotation rate proportional to the increased number of bubbles.
To study the effects of agitation, fine-bubble flotation was conducted at 2,800, 4,300, and 7,000 r/min. The bubble size at each of the three disk rotation speeds is shown in figure 7. The d50’s were 99, 76, and 54 µm for the 2,300-, 4,300-, and 7,000-r/min disk speeds, respectively. Both the 4,300- and 7,000-r/min disk speeds suspended 40 pct air in the pulp, but the 2,800-r/min disk speed had only 20 pct air in the bubble slurry. Motor power measurements at each disk rotation speed increased from 0.3 to 0.5 kW as the rotation speed increased from 2,300 to 7,000 r/min.
The flotation results at the three disk rotation speeds are shown in figure 8. Analysis of variance of the results indicated that the effect of the disk speed was significant at a 95-pct confidence level. Only the minus 5-µm chalcopyrite flotation showed improved recovery with Increased disk rotation speed. As expected from the model, increased agitation and smaller bubbles increased the flotation rate for the minus 5-µm particles. The power measurements showed that increased dissipation energy also resulted in improved flotation of the minus 5-µm particles.
The flotation results for conventional, high-speed conventional, and the three disk speeds for the fine-bubble flotation are shown in figure 9. For the plus 2-µm size particles, the high-speed conventional and 2,800-r/min fine-bubble flotation results were nearly the same, but the high-speed conventional flotation gave better recovery of the minus 2-µm chalcopyrite particles. The d50’s for the high-speed conventional bubbles and 2,800-r/min fine-bubble flotation bubbles were also nearly the same at 97 and 99 µm, respectively. However, the high-speed conventional flotation suspended 29 pct air, and 2,800-r/min fine-bubble flotation suspended only 20 pct air. Again, the increased number of bubbles resulted in better recovery of fine-sized particles. Figure 10 shows the same flotation results plotted as a function of the number of d50 size bubbles per cubic centimeter. The number of d50 size bubbles is the product of the inverse 3 bubble volume and the fraction of air. For ail particle size ranges, the flotation recovery increased as the number of d size bubbles increased. For the plus 5-µm particles, there was no improved flotation above 50,000 bubbles per cubic centimeter. For these larger particle sizes, the probability of collision may have approached 100 pct. Increasing the number of bubbles beyond 50,000 per cubic centimeter would not improve the flotation rate for these size particles.
Conclusions
The extension of turbulent flotation models developed for coarse particles (plus 20-µm size) appears to predict the flotation response of fine particles (minus 20-µm size) also. As predicted by these models, improved flotation response for fine particles was obtained with fine-sized bubbles (d50 99 to 51 µm), a high number of bubbles (50,000 to 800,000 bubbles per cubic centimeter), and increased agitation of the pulp. Fine-bubble flotation recovered more copper than conventional flotation with a near equal or better concentrate grade. At constant airflow the smaller bubbles brought about an increase in the number of bubbles. More bubbles increased the bubble-particle collision probability and improved flotation recovery of the fine-sized particles. Increased agitation raised the bubble and particle relative velocities. This also increased the bubble-particle collision probability and improved the flotation recovery of the fine-size particles. Improved flotation recovery was most evident in the minus 5-µm size fractions. Conventional flotation recovery of the 5- by 2-µm size fraction was only 68 pct, whereas the fine-bubble flotation recovery of that size fraction was 82 pct. Similar results were obtained with the minus 2-µm size fraction.