Many investigators showed that mineral flotation can be described as a first-order process (Sutherland, 1948; Tomlison and Fleming, 1963). In this case, the rate of flotation can be represented by:
dN/dt = -kN……………………………………………………(1)
where N is the number of floatable (or hydrophobic) particles present in a flotation cell and k is the rate constant.
It has been shown that :
k = ¼SbP……………………………………………….(2)
where Sb is the superficial surface area rate of bubbles, which is defined as the bubble surface area moving out of the cell per unit time per unit cross-sectional area of the flotation cell under consideration, and P is the probability of the particles being collected by air bubbles. It can be readily shown that
Sb = 3Vg/R2……………………………………………..(3)
where Vg is the superficial aeration rate, which is defined as the volumetric aeration rate normalized by the cross- sectional area of the flotation column, and R2 is the radius of bubble.
The probability of collection (P) in Eq. 2 can be considered as a product of probabilities of three subprocesses (Sutherland, 1948):
P = PcPa(1 – Pd)…………………………………………(4)
in which Pc is the probability of bubble-particle collision, Pa, the probabilities of adhesion, and Pd is the probability of detachment.
For an air bubble rising under quiescent condition, Pc can be determined by a stream function of the fluid flowing past the bubble. Yoon and Luttrell (1989) derived an empirical stream function:
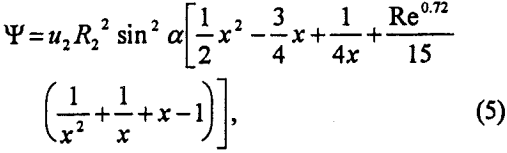
which is applicable for the range of bubble sizes used in flotation practice. In Eq. 5, u2 is the bubble rise velocity, x is the radial coordinate (r) normalized by R2, i.e., x=r/R2, and α is the angular coordinate. From Eq. 5, Yoon and Luttrell (1989) derived an expression for Pc as follows:
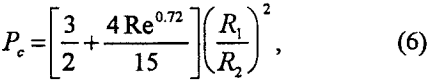
in which Rl is the radius of particle to be floated.
For the probability of bubble-particle adhesion (Pa), Luttrell and Yoon (1992) suggested the following expression:
Pa = exp[-El/Ek]…………………………………………………….(7)
in which El is the energy barrier for the bubble-particle adhesion, and Ek is the kinetic energy of collision. Eq. 7 is analogous to the theory of chemical reaction rate. The values of Ek can be calculated from the tangential velocities of the particles moving around a bubble. For bubble- particle interactions occurring under quiescent conditions, the tangential velocities can be obtained from the stream function (Eq. 5) (Yoon and Mao, 1996).
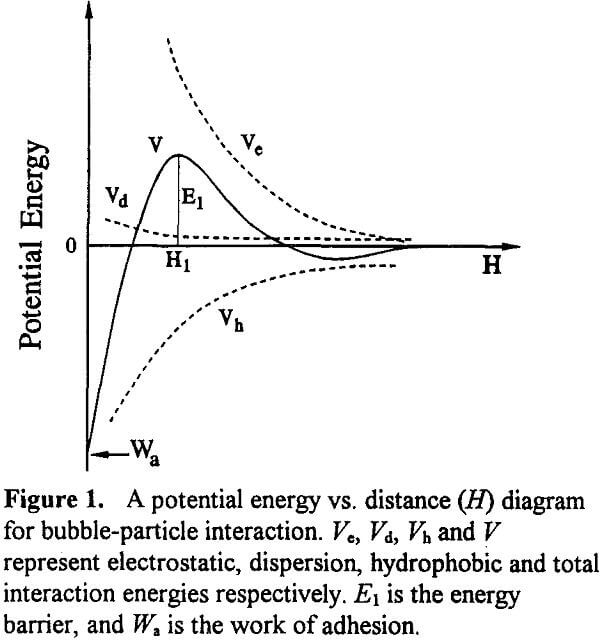
Figure 1 shows a typical potential energy vs. distance diagram for bubble-particle interaction. The overall interaction energy (V) is determined by the following relationship:
V = Vc + Vd + Vh………………………………………….(8)
where Vc, Vd, and Vh, represent the interaction energies due to electrostatic, dispersion and hydrophobic forces, respectively. As is well known, Vc is always repulsive for bubble-particle interactions. When Vc is repulsive, the hydrophobic force is the only driving force for the bubble- particle adhesion.
For bubble-particle interactions, Vc can be determined using the following expression (Hogg et al., 1965):
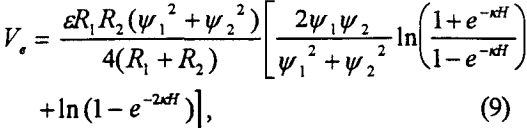
where Ψ1 and Ψ2 represent the Stem potentials of the particle and air bubble of radii R1 and R2, respectively, ε is the dielectric constant of the medium, and l/k is the Debye length.
Vd, on the other hand, can be given by the following relationship (Rabinovich and Churaev, 1979):
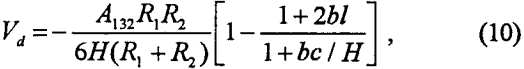
where A132 is the Hamaker constant for particle 1 interacting with air bubble 2 in medium 3 (water), while b, l and c are constants. Usually, A132 is negative; therefore, dispersion forces are repulsive for bubble-particle interactions.

