Table of Contents
The rare-earth metals can be fitted into Pauling’s electronegativity scale if it is modified to take highly ionic bonds into account. Good agreement between theory and experiment is obtained only for metals of groups Ia, Ila, and IIIa of the periodic table, but here it is good enough to permit estimation of unknown heats of formation. For compounds which are highly ionic, the results agree well with other estimates. For compounds that are mainly covalent, the results are lower than the best available estimates. This may be due to underestimation of the heat of assembling the molecules into crystals.
Electronegativities of the rare-earth elements were calculated from heats of formation. The values obtained from different compounds varied widely. The postulates of Pauling’s electronegativity theory were interpreted for bonds that are primarily ionic; the study showed that many compounds obey rules of the form expected. Revised electronegativity values are given for the more electropositive elements, including the rare-earth metals (which are near magnesium in electronegativity). Estimates of unknown heats of formation are made from electronegativities and are compared with other estimates.
Calculation of the electronegativities of the rare-earth elements is interesting to show how these metals stand relative to the other metals and to each other, and also possibly to systematize the thermochemical data on them.
Pauling has described his electronegativity scale in detail; briefly, it is constructed as follows:
- The usual 2-electron chemical bond is assumed to be the result of resonance between a completely covalent structure and a completely ionic structure. The energy of the bond is greater than that of either extreme because of the stabilizing effect of resonance.
- The heat of formation of a covalent single-bonded compound from covalent single-bonded elements is assumed to be zero. The energy of an actual bond thus arises from its partial ionic character and is termed the “extra ionic resonance energy.”
- The elements in their standard states are assumed to be covalent single-bonded except for oxygen and nitrogen;, for which corrections have been calculated.
- Electronegativities are assigned to the elements. The electronegativity differences are made approximately equal to the square roots of the heats of formation in electron volts per bond.
In assigning electronegativities to a number of the elements, actual bond energies were used rather than heats of formation.
Results
The electronegativities of the rare-earth elements were calculated using heats of formation from a recent review. The calculated electronegativities were not consistent; for example, lanthanum ranged from 0.9 to 1.6, depending upon the anion. Although the calculated electronegativities usually increased slightly with atomic number, those obtained from the oxides decreased. Other electropositive metals exhibited similar discrepancies.
An attempt was made to treat these metals more adequately within the framework of the electronegativity theory. Pauling estimated that 50 percent ionic character was reached at an electronegativity difference of about 1.7, and remarked that calculated bond energies are too large when electronegativity differences are greater than 1.5.
Since resonance energy is a maximum when the contributions of the resonating structures are equal, it should decrease as the electronegativity difference becomes very large, and the compound becomes primarily ionic. At the same time, the large contribution of the ionic bond shows that its energy is greater than that of the corresponding covalent bond. This greater energy will tend to offset the decreased resonance energy. Qualitatively the bond energy should increase less rapidly with electronegativity difference when the latter becomes large, and may even decrease when the difference is large enough. If these factors are taken into account, the assigned electronegativities must be changed.
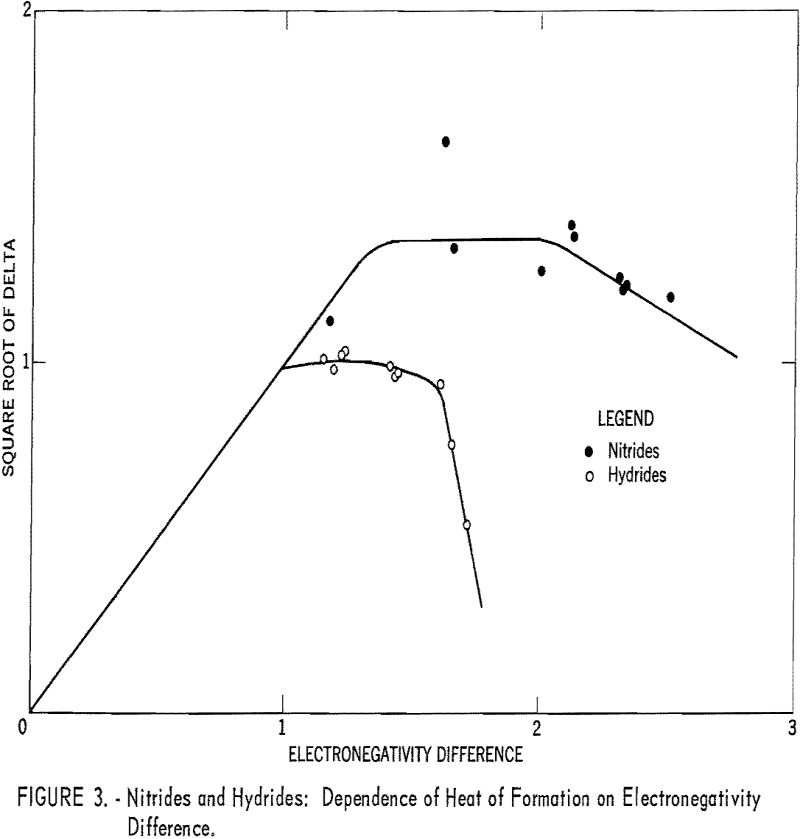
Plots of the square roots of heats of formation versus anion electronegativity were made. Then the origins of the graphs were shifted horizontally until the curves coincided. The regions of the curves where abscissa and ordinate were equal then allowed the electronegativities to be calculated.
The heats of formation of rare-earth and yttrium compounds were taken from a review, those of scandium compounds from Brewer and coworkers, that of aluminum chloride from Coughlin, and the others from Circular 500. The scandium values are expected to be too large. The heat of formation of anhydrous cerous fluoride, obtained by assuming its free energy of hydration to be zero, is -403 kcal./mole; that obtained from the Brewer and coworkers estimate of its heat of solution and the results of Spedding and Miller is -409.5 kcal./mole. The latter value was used.
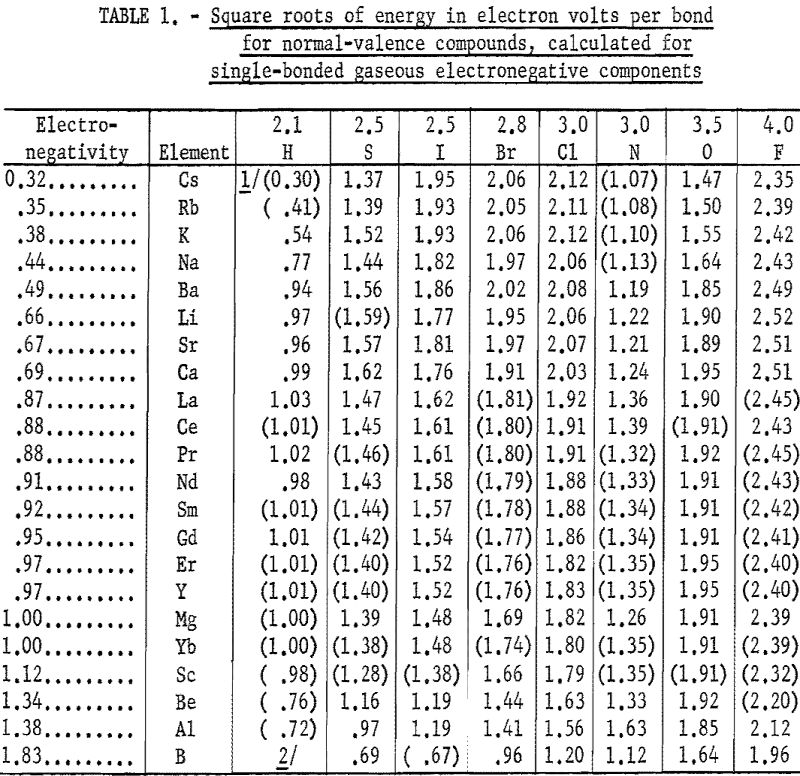
The heats of formation in table 1 and figures 2, and 3 were calculated in electron volts per bond (symbol Δ). Corrections to the covalent single-bonded state were taken from Pauling. To minimize effects due to differences in standard states, those for bromine, iodine, and sulfur were taken as Br2(g), I2(g) and S8(g). These standard states are used only for calculating Δ values; the Δ Hf° values refer to the conventional standard states. The conversion is made by:
![]()
where n is the number of atoms of each element in the compound and the summation of Δ is over all bonds in the molecule. The calculation of Δ for BaBr2 is, for example, from equation (1):

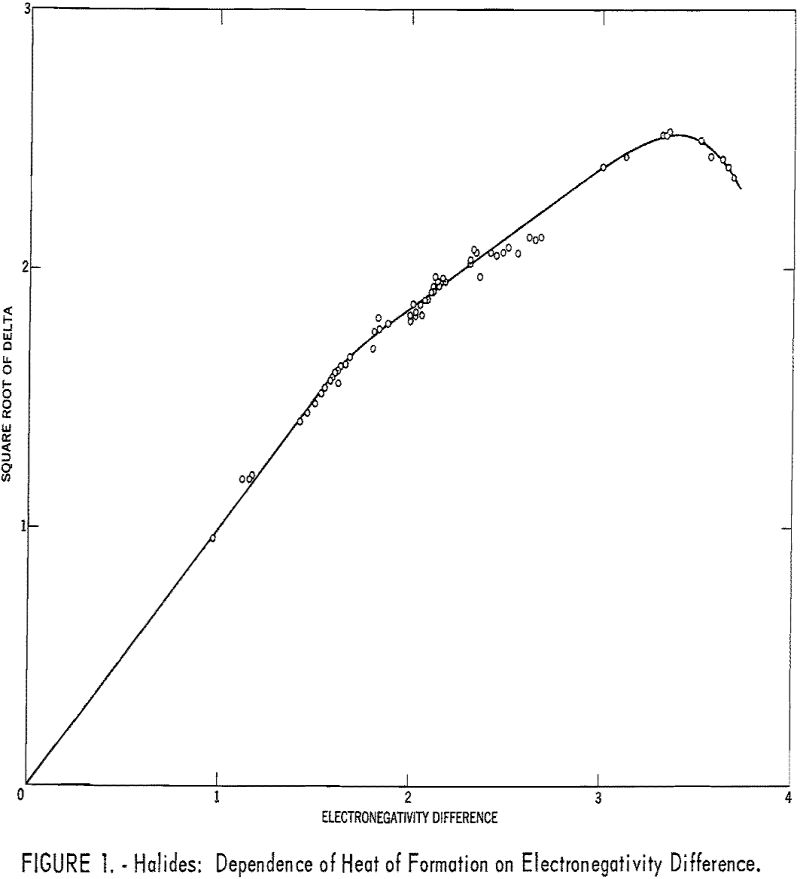
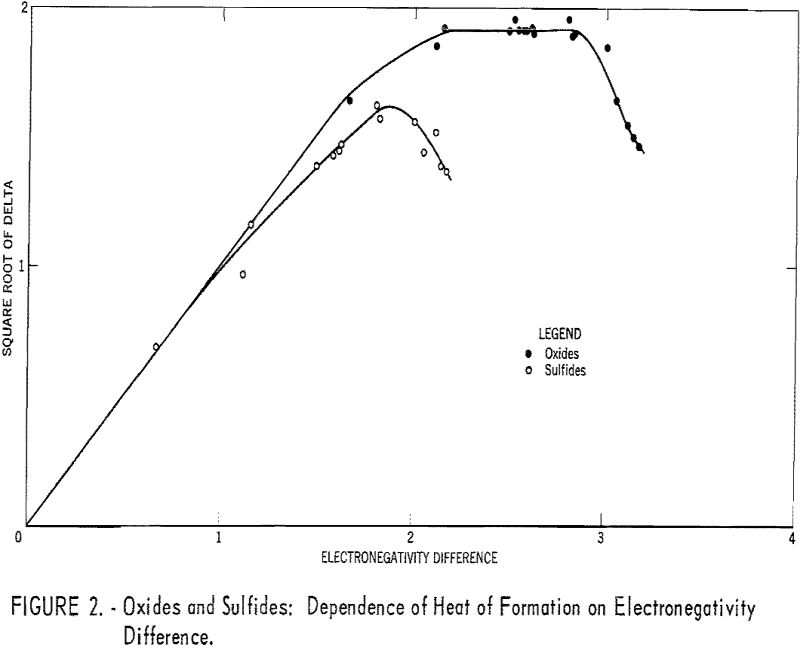
Table 1 gives the results obtained and plotted in figures 1, 2, and 3. Values in parentheses have been interpolated from the curves of the plotted figures.
Discussion
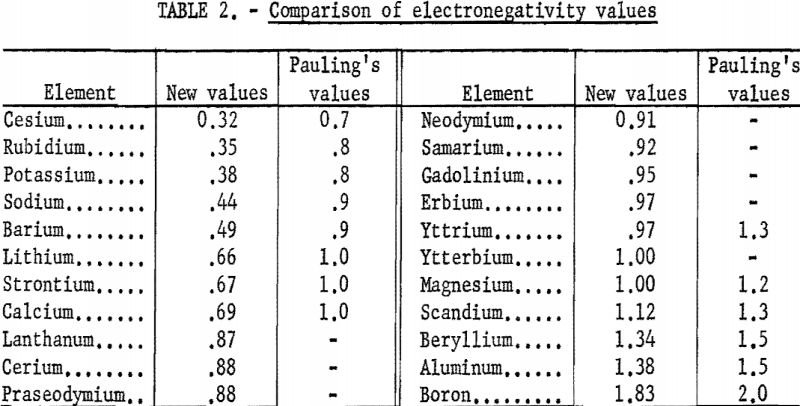
The new electronegativity values are compared with Pauling’s in table 2. The new values are smaller and show more difference between the metals. The rare-earth metals fall between calcium and magnesium, being closer to magnesium.
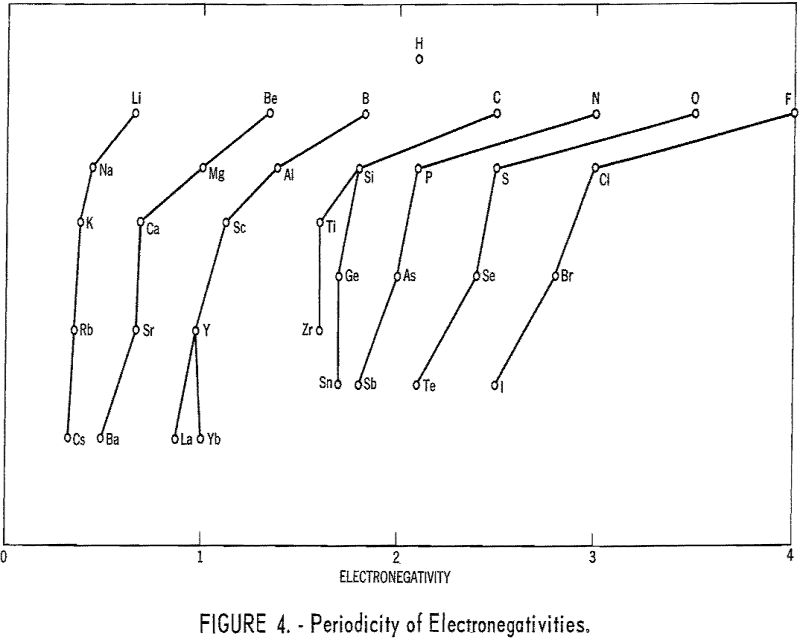
The method used here works very well for the 21 metals in tables 1 and 2. For the other metals, it does not appear to be applicable. The success in the case of the metals considered may be a result of the facts that they have only one important valence each and that their normal ions contain no d electrons in the outermost shells. Thus the situation is much simpler than in the case of most transition metals. Figure 4 shows the relationship between electronegativities and the periodic table.
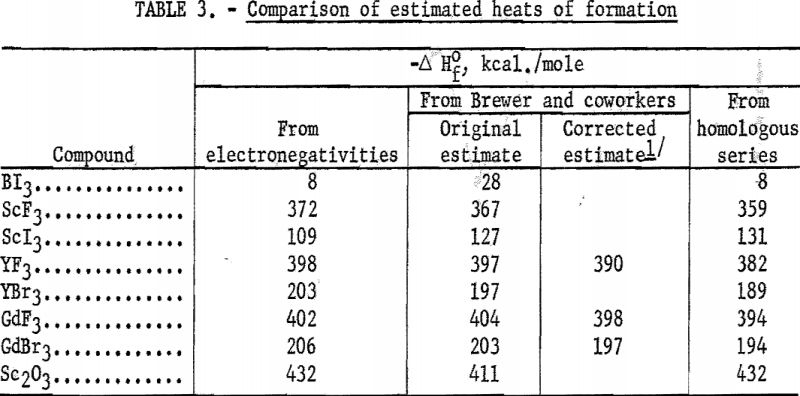
The average deviation of Δ from the curves is less than 0.03; thus these curves may be used to estimate heats of formation. Table 3 compares estimates of some heats of formation from electronegativities with the results of other estimation methods. The estimates of Brewer and coworkers for BI3 and YBr3 are probably the most reliable, since they estimated lattice energies rather than directly estimating heats of formation. In the other cases they used estimated heats of solution. However, some experimental data that they used for the rare-earth compounds are too high. The only serious discrepancies between the electronegativity estimates and those of Brewer and coworkers are for the iodides and scandium oxide.
The estimation of heats of formation from homologous series and from volume changes have been discussed by Kubaschewski and Evans.
In figure 5 the heats of formation of the halides and oxides of the group Ilia metals are plotted. For the halides, a method of plotting suggested by Yates has been used. The heats of formation were plotted against the atomic numbers of the metals, and the curves then were moved parallel to the atomic number axis, keeping the points for aluminum in a straight line. (Aluminum is the only group Ilia metal for which the heats of formation of all the halides are known.) The 3-dimensional representation thus obtained allows the
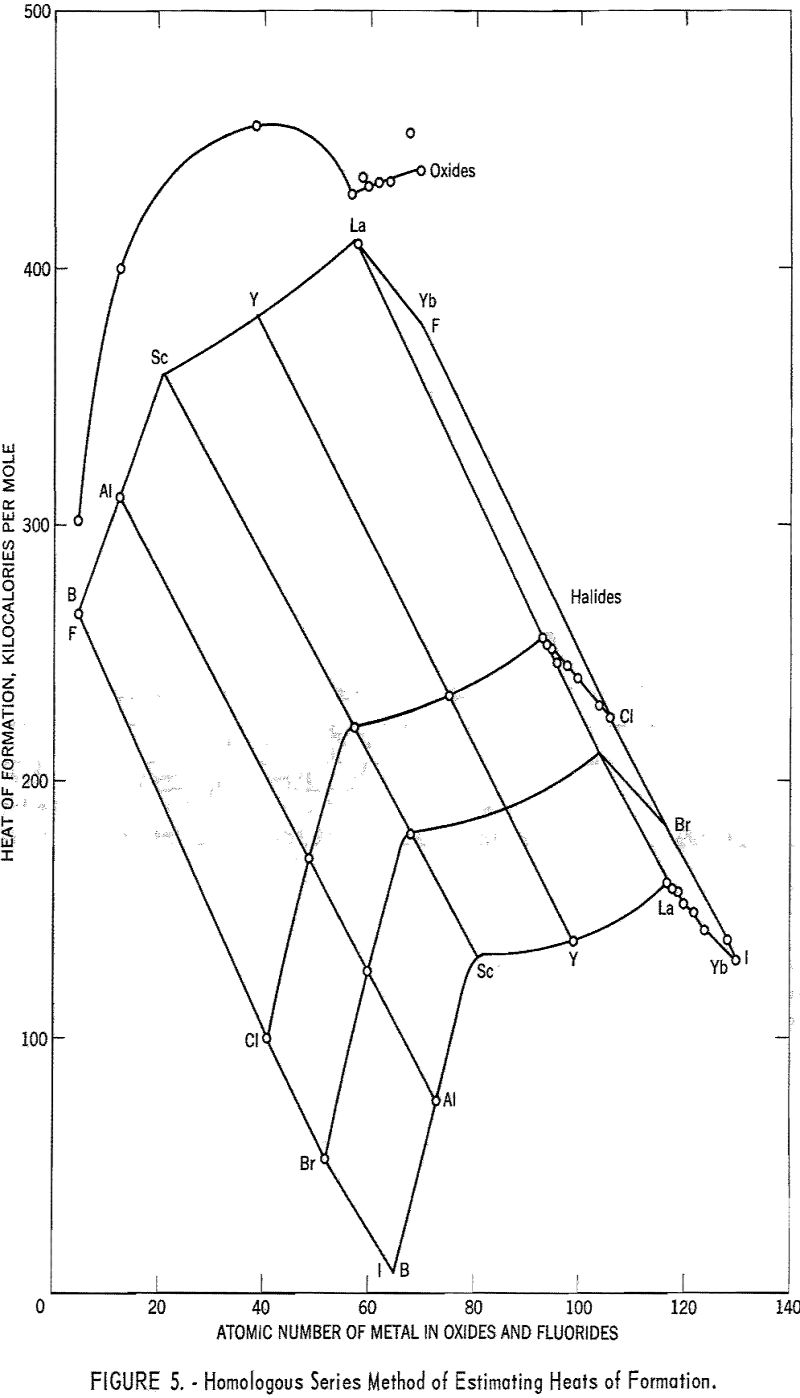
variations with anion and cation to be considered simultaneously when the missing heats of formation are interpolated.
In the volume change method of estimation the heats of formation are plotted against percent volume contraction in formation, all densities being those of the solid state in close-packed structures. For the metals, which often crystallize in close-packed or nearly close-packed structures, experimental data usually can be used. For the halogens, oxygen, nitrogen, etc., the densities must be estimated using approximate corrections for the variation of ionic radius with coordination number. Unless factors to correct the densities of the compounds to those of close-packed structures are known, a separate plot must be made for compounds of each structural type.
No adequate plots could be made for compounds in table 3 because of the small number of compounds of each structural type for which the necessary structural, density, and thermochemical information is available.
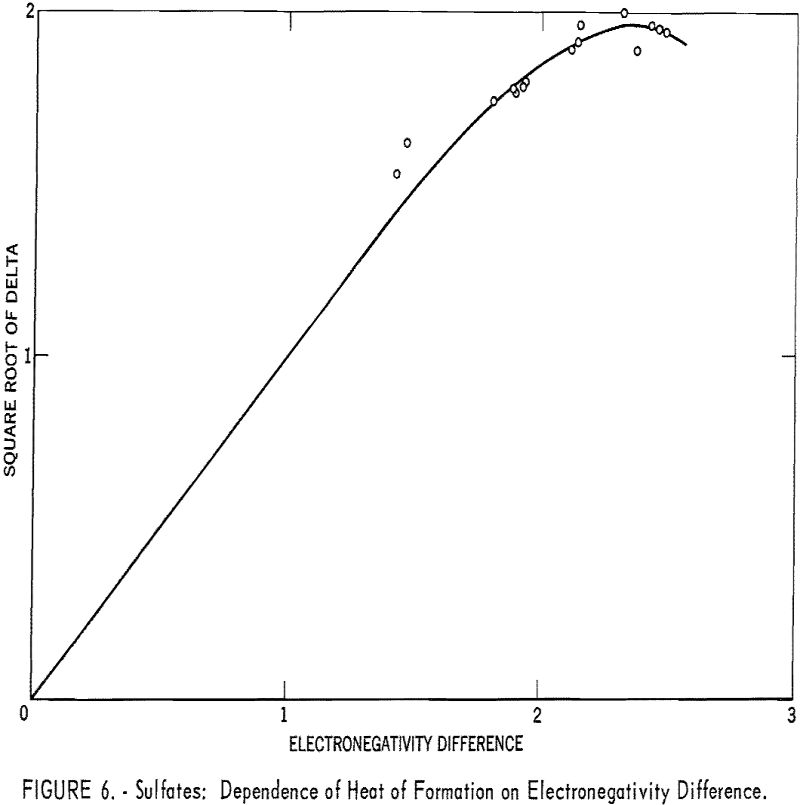
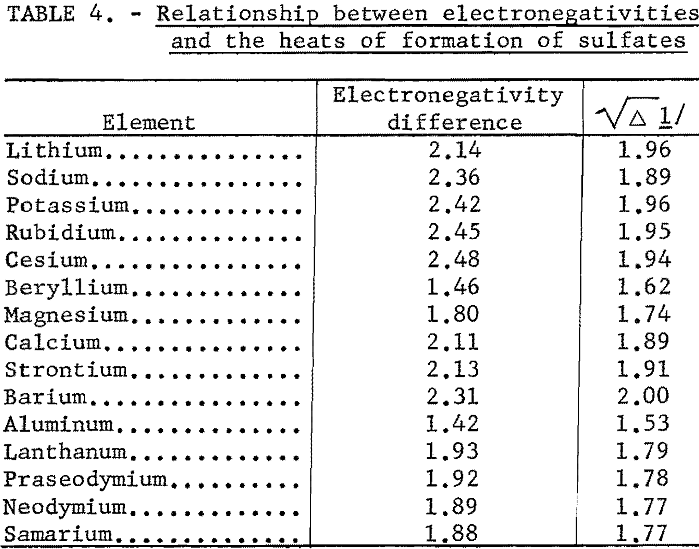
Even an ion such as sulfate can be treated by the electronegativity method. When the sulfate radical is assigned a hypothetical covalent single-bonded heat of formation, -165 kcal., and an electronegativity of 2.8, the correlation shown in table 4 and figure 6 is good.
Factors affecting the accuracy of the electronegativity treatment are:
(1) Errors in the fundamental postulates. These have been discussed by Pauling; (2) the change of heat of formation with temperature; the theory should apply at 0° K.; (3) neglect of the heat of vaporization of the compounds.
This appears to be the most likely source of the discrepancy with Brewer’s estimates. The heat of vaporization makes compounds more stable than would be calculated from their bond energies alone. This factor will be most important, percentagewise, in the case of the smallest heats of formation, such as those of the iodides. The empirical approach used in constructing the curves should partly cancel out the effect.
It should be emphasized that the correlation described in this paper is empirical and does not indicate that the postulates of the electronegativity theory are necessarily correct.