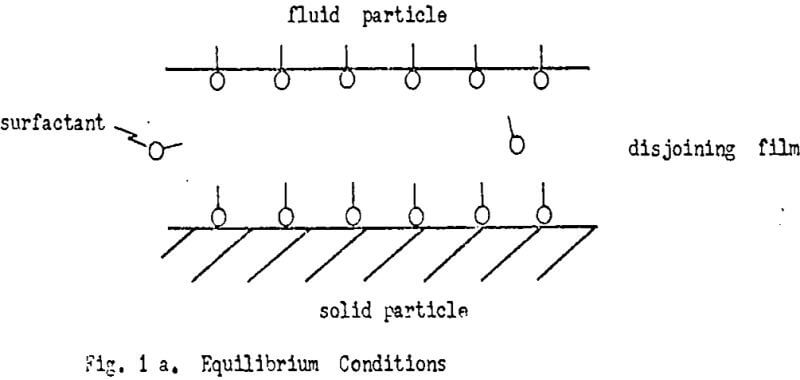
Rendering a solid hydrophobic and solid-fluid particle attachment in flotation are recognized is not necessarily related. The attachment is governed by forces of attraction and repulsion which need to be considered. The induction time required for attachment after solid and fluid particle are brought into proximity illustrates the point.
Thinning and Rupture of the Disjoining Film
The major recognized interacting forces result from the electrical double layer of the solid and fluid particle (πel) and the cohesive/adhesive forces of the solid/water/fluid system. The cohesive/adhesive forces can be summarised in the Van der Waals force(πvan).
Derjaguin introduced the concept of a disjoining pressure (π) which may be defined as the net force of attraction per unit area of film:
π = (1/A δw/δh)equilibrium
where A = film area
w = free energy of interaction of solid and fluid particle
h = film thickness
Given that πel, and πvan are complex functions of h, and assuming additivity
π = πel + πvan
Interfacial Tension Inequalities (Δγ)
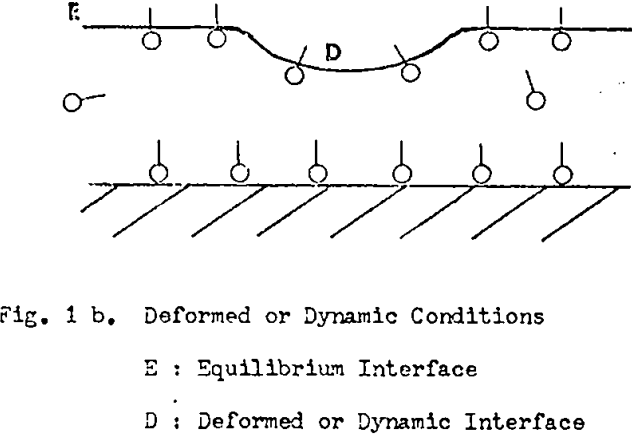
From inspection of Fig. lb the following can be written:
ΓD < Γ E
and γD > γE (with surfactant)
where Γ = interfacial surfactant adsorption density
γ = interfacial tension
E = equilibrium interface
D = deformed or dynamic interface
For convenience the interfacial adsorption density and interfacial tension inequalities will be considered separately. Firstly, the consequences of the interfacial tension inequalities will be examined.
The higher tension at the deformed interface will cause an elastic recoil (Gibbs elasticity). The interface is pulled towards the region of higher tension, thus tending to damp out the fluctuation. The lower interfacial energy region, in fact, spreads at the expense of the higher energy region in accordance with thermodynamic principles. This spreading creates a flow in the underlying film 28, (the Marangoni effect) which, therefore, opposes film drainage. Such a flow is considered responsible for interfacial turbulence and dimple formation in fluid-fluid coalescence.
The degree of film stabilization contributed by the condition γD > γE will increase with the magnitude of (γD – γE) = +Δγ and on the rapidity with which +Δy is eliminated by interface and bulk mass transfer tending to restore equilibrium.
For the interfacial tension inequality to promote film drainage, γD < γE. In the presence of surfactant this requires ΓD > ΓE.
The condition ΓD > ΓE or γD < γE can arise if mass transfer of the surfactant from the fluid particle to the water occurs. Due to the confines of the film surfactant concentration in the film tends to exceed that of the water bulk. Thus, upon deformation, the bulging interface encounters a higher surfactant concentration than the unperturbed interface.
When an interface is nearly flat any normal force will cause some deformation. Under conditions where the gas bubble is replaced by an oil droplet, γ will be reduced thus, relatively, F becomes larger. This might favour oil droplet flotation under conditions where gas bubble flotation fails. However, the need to account for mass transfer inside the oil droplet may render the above estimate of F in error for the oil droplet flotation system.
The bulk of flotation research is directed at understanding the properties of the solid-water interface. This recognizes that selective mineral flotation results from differences in mineral-water interfacial properties since the fluid particle-water interface is, presumably, common to all the minerals in the slurry.