Discrepancy Between Actual and Expected Recovery: Gold Metallurgy Accounting

Everyone connected with cyanide plants has at some time or another been confronted with a real or apparent shortage of bullion in the clean-up, that is, the bullion recovered has been less than the amount expected when calculated from the assays of head and tail and the tonnage treated.

Such a shortage will often occur at the end of the first months run of a mill and is easily accounted for. First, there may be an absorption of metal-bearing solution by the Dew woodwork and filtering medium; second, there may be mechanical losses by leakage, due to joints in wooden containers not yet having closed under the influence of the moisture, and also to run-overs which may easily happen during the process of getting a new plant and its shifter settled down to their working routine. If precipitation is done by zinc shavings, a large quantity of the precious metals first dissolved will be needed to coat the surface of the zinc in the boxes before a nonadherent deposit is formed which can be cleaned-up and melted.

Again, the relation between the amount of bullion found and the amount calculated as due for the first month is complicated by the difficulty of assigning to a given month its exact quota of ore and pregnant solution. For instance, take the case of a sand leaching plant where the treatment of a charge extends over 10 days; it will be obvious that if the collecting of a sand charge begins on the first of the month and one charge is collected every 24 hours, then by the end of the month, 31 charges of, say, 100 tons each, will have been collected, but only 21 of them will have been completely treated and discharged from the plant; the other 10 will be in various stages of advancement. No. 22 will perhaps be just finished and ready to go to the dump, 23 will be in the water wash stage, 24 in the weak solution wash stage, until when we reach No. 31 we find it has had no treatment at all and has as yet yielded up nothing of its valuable contents. It is thus evident that if the calculation for recovery is made on the tonnage of ore milled and collected during the first month, the bullion cleaned up will fall very far short of the amount called for.

Now suppose that to obviate this difficulty it is decided to calculate the amount of bullion due by taking account only of such charges as have already finished their treatment and been discharged from the plant. In this case the bullion cleaned up should be in excess of that calculated because the charge collected on the last of the month will not have finished its treatment till the 10th of the following month, consequently the first months clean-up will contain not only all the precious metal contents of its own thirty-one days, but all of that belonging to the charge of the first day of the following month, practically all of that of the second, most of that of the third and so on in diminishing amounts to the 10th day when the clean-up has taken place. Thus whatever method of computation be adopted it is almost impossible to ascertain the true quantity of bullion that ought to be expected as the result of the first months work. The same principle may be applied to slime treatment, whether continuous or intermittent.

It may be laid down then as a general principle that no importance whatever need be attached to the relation between calculated and actual recovery during the first months run of a mill.

These are 1910 dollars. Use https://www.usinflationcalculator.com/ to convert to today.

When a mill is well under way the high officials of the Company usually expect the bullion returns at the end of each month to check with the calculated amount due, but here again there are legitimate reasons why this may not always happen. One such reason lies in the computation of the tonnage treated. This is most often arrived at by weighing or estimating the amount of ore fed to the mill bins during the month. As there is nearly always a carry-over of ore from one month to another, this method involves an estimation of the amount remaining in the bins on the last of the month, which may or may not be correct. Another method of obtaining the tonnage is to determine it by specific gravity of slime pulp collected or discharged, or in the case of sand, by cubic capacity. Both these methods are open to small errors even when great care is exercised, but they get away from the necessity of guessing the amount of ore held over in the bins.

Again, the difficulty observed during the first month of milling is apparent in a less degree in the case of subsequent individual months, namely that of drawing a clear line between the tonnage, head assay, tail assay, and gold and silver precipitated, belonging to any two adjoining months. With ore of uniform assay value the resulting difference would be small but with ore whose contents are of a variable and patchy nature, it may be considerable.

If zinc shavings be used as the precipitant the quantity of bullion held over in the boxes may be a variable quantity, due to differences in the method and thoroughness of dressing them. If the quantity of zinc is allowed to become low toward the end of a month, there will be a greater recovery of bullion than would be the case if the boxes were well packed with new zinc a few days before the clean-up.

It will thus be seen that it may often legitimately happen that the bullion recovered at the end of a given month may be less than the amount called for by a calculation of tonnage and assays. If, however, there is nothing radically wrong with the methods of computation, such losses on individual months should be balanced by corresponding gains in other months, and at the end of a year or, say, six months, the total actual recovery should tally very closely with the calculated one. Should this not be the case, it will be obvious that all is not right, and that investigations are called for.

When such a discrepancy really exists there are six possible ways of accounting for it: (1) Theft, (2) carelessness, e.g., losses of solution by run-overs and losses of precipitate by careless handling in cleaning up and melting, (3) errors in tonnage computation, (4) errors in sampling of ore heads, (5) errors in sampling of residues, (6) errors in the assaying.

Of these various possibilities (1) is probably comparatively rare; (2) should be inconsiderable if proper supervision is exercised, though there must be always a small unavoidable loss in cleaning up and melting; (3) and (4) are in the writers experience the most fertile causes of serious discrepancy; (5) should not be a factor if ordinary care and intelligence are exercised; and (6) needs careful watching.

Plant Tonnage Measurement

In some mills every car or the belt conveyor if such be in use, passes over an automatic weighing and recording scale and this method comes nearest of any to giving a correct determination of the tonnage, but even here an error may creep in due to faulty correction for moisture. The percentage of moisture in the current ore is usually taken as a fixed quantity, and the amount is more often guessed at than ascertained. Even when an honest attempt is made to obtain a correct average figure for moisture, the determination is by no means easy. Ore from different parts of the mine is liable to vary over wide limits in its moisture content, and the season of year may make a difference in the ore from any given stope. And if there is an opening for discrepancies in tonnage under the weighing system, what is to be said of the more common practice of taking the buckets or cars at a fixed and arbitrary weight and multiplying by the number passed into the mill during each day?

Probably the best way to estimate average moisture in the ore fed to the mill is to weigh a whole bucket load at intervals and at once dry it on a flat-sheet supported on bricks, over a slow fire, weighing it again when dry. If two or three buckets are treated in this way every second day for a week or ten days a fairly good idea may be obtained of what correction ought to be made, and an average thus arrived at. Similar determinations should be made both in the dry and the wet seasons. If ore in different parts of the mine varies greatly in its water content, separate estimations of each kind of ore should be made and the number of cars of such ore during the day or month noted. If a sample of this dried ore be taken and tested for moisture after, being pulverized in the laboratory, a further reduction in weight may often be recorded amounting to 1 % or over.

Another method commonly made use of for arriving at the monthly tonnage is to estimate it from the ore pulp in the cyanide plant, the sand (if leaching is in use) being calculated from the cubic contents of each charge, and the slime by the specific gravity and measurement of the slime charges. If these operations are performed with proper precautions and due care, a close approximation to the correct tonnage may be obtained but it is very easy for serious errors to creep in. Regarding the sand charges the weight of a cubic foot of sand varies over wide limits according to the method of filling and the specific gravity of the ore The same ore may vary from 19 to 30 cubic feet per ton according to (1) whether the charge is measured in the tank in which it was collected or after being transferred to another tank, (2) (if measured after transferring) whether such transfer is made by shovelling or mechanical devices, (3) whether such measurement of transferred sand is made before or after applying solution, (4) (if measured in the collecting tank) whether it be collected by one or another of the various methods described, (5) whether the sand be charged dry or moist. Thus, in order to avoid error the weight per cubic foot should be carefully and frequently determined.

Another source of error may arise in the measurement of vertical depth of each charge owing to the fact that the surface is never level as a whole, nor is it free from small irregularities at the point of measurement making it difficult to decide within an inch or so at what point to begin measuring.

In the slime treatment it is difficult to estimate tonnage with the continuous system but in the charge system it may be done very closely, if the following precautions are observed:

1. The specific gravity of the dry slime must of course be accurately determined.
2. In ascertaining the ratio of liquid to solid in any given charge the sample taken must be representative. As a rule the thicker a pulp is, when in agitation, the more homogeneous it is. From a slime charge with a dilution ratio of 3 or 4 to 1 in an ordinary mechanical stirring tank, samples may be taken at different points which show widely differing ratios of liquid to solid.
3. Correct measurements of the cubic content of the charge must be made. This cannot be done while the charge is in motion. Moreover, allowance has to be made for permanent solid material occupying space in the tank, especially hard rings or cones of slime, sand, etc., and also (in the case of flat bottom tanks) a certain depth of treated pulp which it is impossible to remove each time the tank is emptied.

Tonnage of Pulp, as Ascertained by Density Determination

This method depends on the cubic capacity of the slime charge and its density as determined by specific gravity test. Specific gravity may be explained as the ratio between the weight of a given substance and the weight of the volume of distilled water at 4 degrees C. displaced by it. The first requisite is to find the specific gravity of the dry ore-pulp. For this purpose dry some of the powdered material over a water bath or at a temperature not exceeding 100 deg. C. (212 F.), and at once weigh up carefully 250 grams and place in a dry litre measuring flask which has been previously weighed and the weight recorded. Then add about 500 cc of distilled water and mix well. The dry ore nearly always contains a large quantity of air adhering to the particles which is very difficult to detach and therefore Clennell recommends immersing the flask in boiling water and keeping it at that temperature for from one to two hours in order to expel all the air. It is then cooled, and distilled water added up to the mark, after which the flask with contents is weighed and the weight of the empty flask deducted, the object being to ascertain the weight of the water which has been displaced by the ore.

To do this the weight of a similar volume of distilled water must be known. A litre flask contains nominally 1000 grams of water but it is better to empty the ore pulp out of the flask and after washing well to refill with distilled water at the same temperature as was the water used for mixing with the ore sample, and after drying the exterior of the flask to weigh carefully. This figure less the recorded weight of the dry flask is then compared with the weight of the same volume of the ore-and-water mixture previously found.

Let a = weight of dry ore taken
b = weight of water in the flask when filled to the mark with water alone
c = weight of mixture of ore and water at the same mark
d = weight of water in the mixture
w =  weight of water displaced by the dry ore
s = specific gravity of dry ore

Then c – a = d
and b – d = w
and s = a/w
or s = a/a+b-c

If great precision is required, the mixture of ore and water, and also the water alone, should be cooled to 4 deg. C. in the flask and weighed at that temperature, the level of course touching the mark in each case, but for ordinary purposes it is sufficient that the temperature at both weighings should be that of the atmosphere.

To determine the specific gravity of the wet pulp composing the slime charge it is more convenient to use a litre flask whose neck has been cut off about an inch above the mark, or better still to procure such a flask properly finished off by the manufacturer. This is weighed empty and then filled to the mark with the pulp to be tested. A representative sample should first be taken in a bucket and the ratio of water to ore should be low, that is, the pulp should be as thick as possible to ensure homogeneity. The sample is then thoroughly mixed and kept in agitation while portions are dipped out with a small beaker, and poured into the flask taking care that no settlement takes place in the beaker during the operation. This is continued until the level reaches the mark on the neck. The flask is then dried (if wet on the outside) and weighed, and the weight of the empty flask deducted from the figure found.

Then if W1 = Weight of pulp.
W2 = Weight of same volume of water.
W 1/W2 = Specific gravity of the pulp.

For calculating the quantity of ore in the charge from this figure, Clennell gives the following formula:

V¹ = 32 (S – 1)/S(P – 1) or V = 35.31(S – 1)/S(P – 1)

where V¹ = Number of cu. ft. of pulp to 1 short ton of dry slime.

V = Number of cu. ft. of pulp to 1 metric ton of dry slime.
S = Specific gravity of dry slime.
1 = Specific gravity of solution.
P = Specific gravity of pulp.

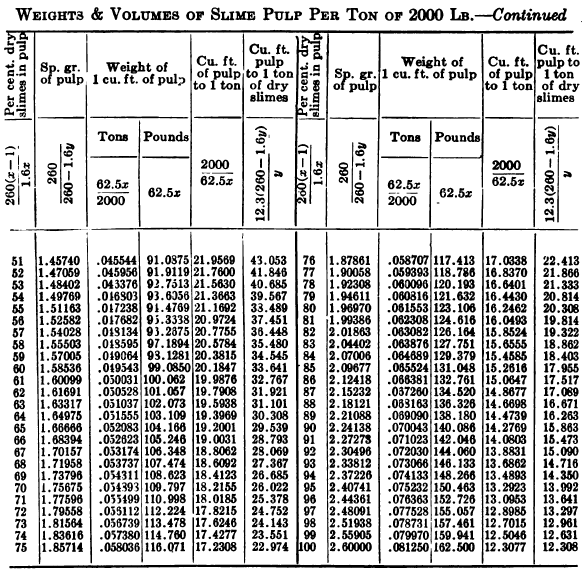
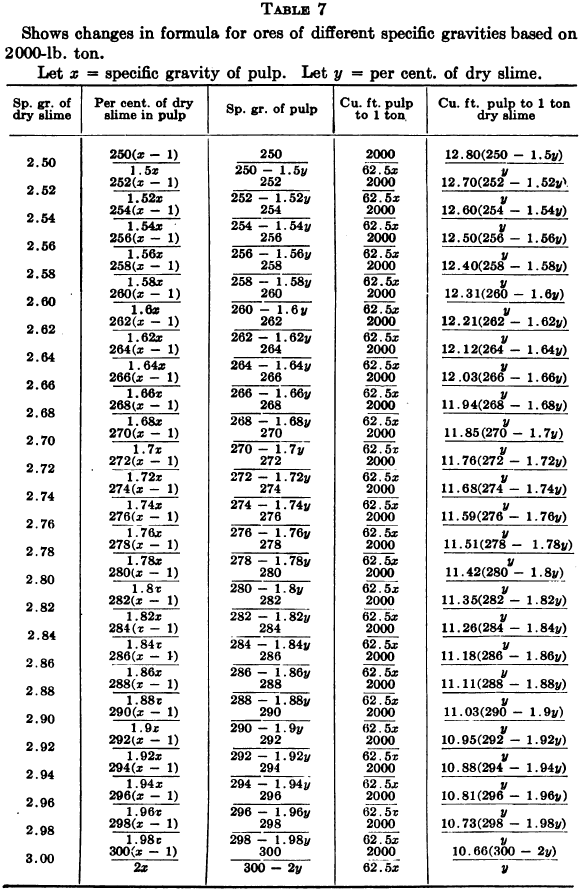
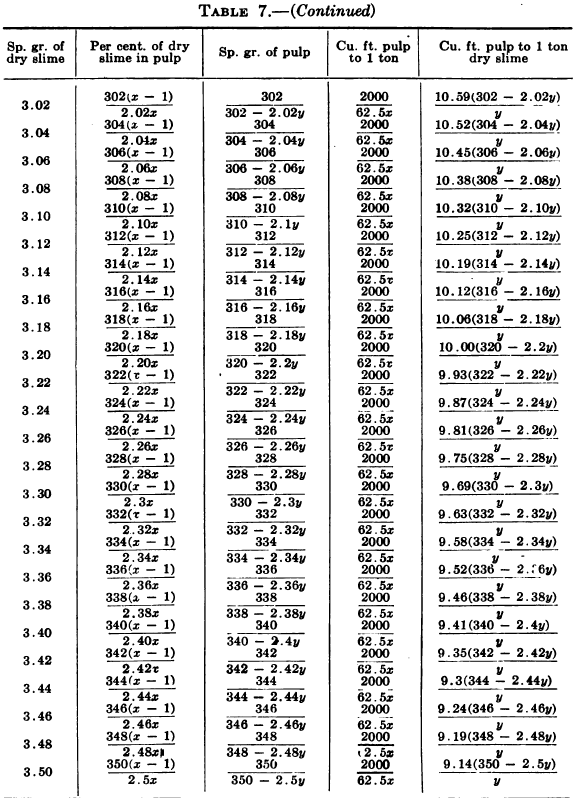
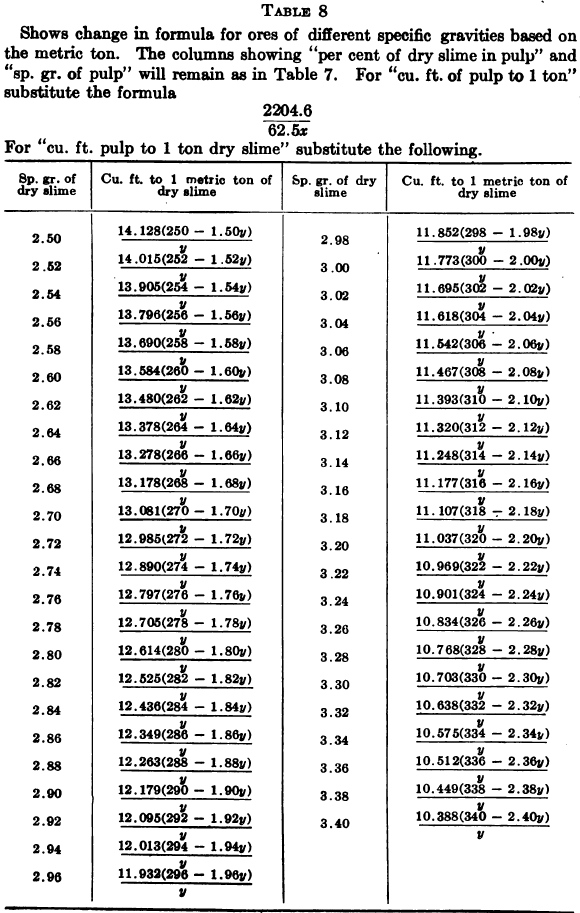
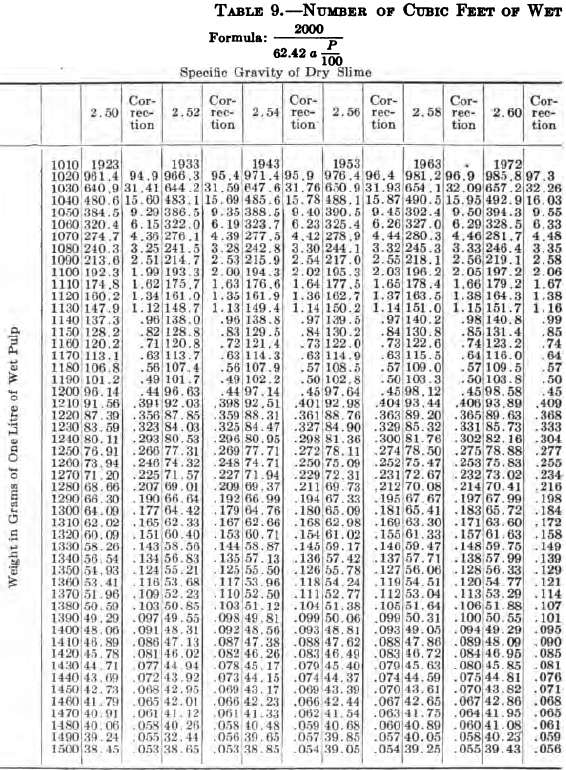
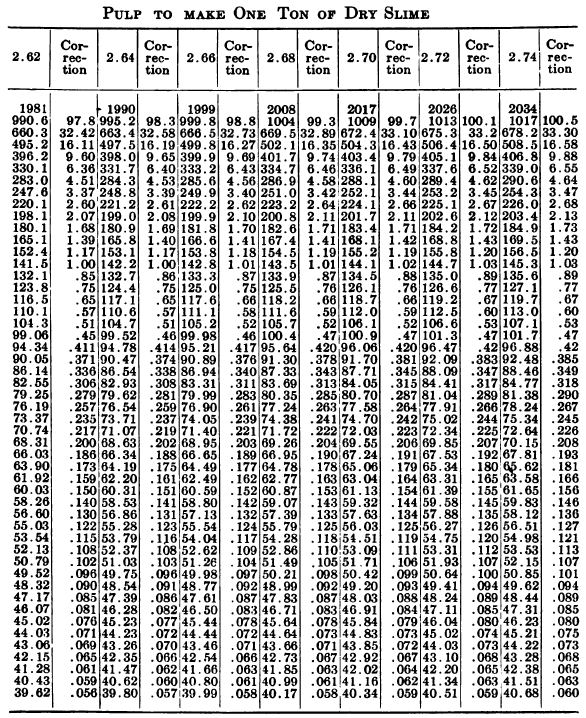
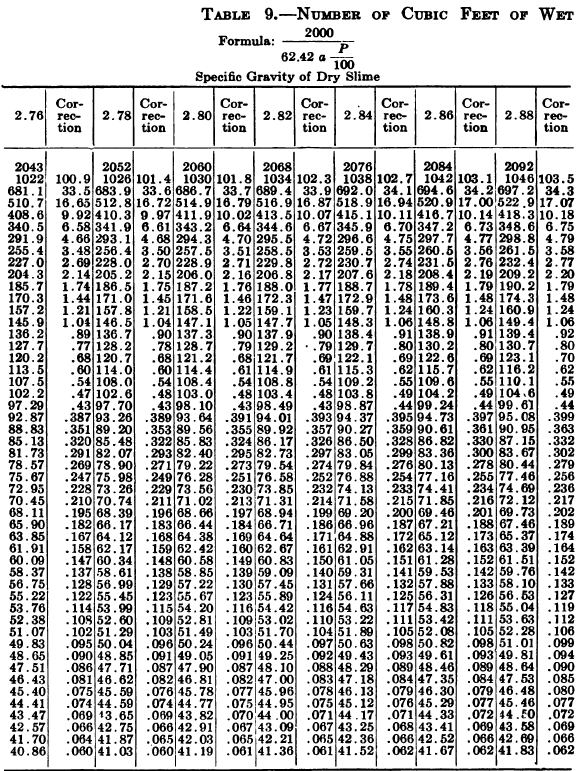
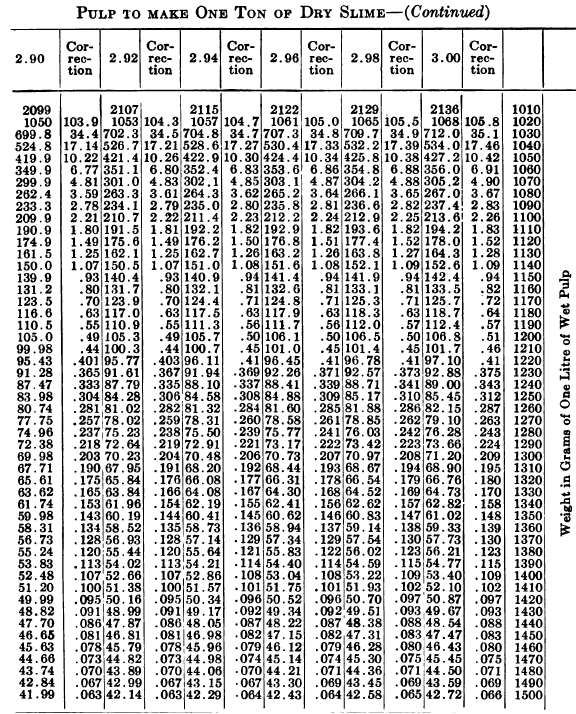
W. A. Caldecott’s pulp table with one or two slight changes in the formulas is here given in full, based on a specific gravity of 2.6 for the dry ore. A second table follows, showing the changes in the various formulas in the preceding table for specific gravities from 2.5 to 3.5, so that a complete table may be drawn up for each mill according to the specific gravity of its ore.

Possible Met Accounting Error Due to Density of Solution

A source of error that may in certain circumstances assume more than negligible proportions lies in the fact that, in most of the calculations of slime density, the specific gravity of the solution is taken to be 1, as it would be if it were pure water, but it is obvious that the various substances in solution, such as lime, cyanide, zinc, and soluble constituents derived from the ore, will raise the specific gravity above that of water. In the case of simple clean ores, which require only weak solutions of cyanide and lime, the error due to this cause may be neglected but when dealing with more complex ores and more concentrated solutions it may materially modify the monthly ore tonnage as determined by this method. An article by G. H. Clevenger, H. W. Young, and T. N. Turner, in the Engineering and Mining Journal of December 19, 1914, deals with this subject in considerable detail.

A list is there given of the specific gravities of the solution from a number of mills, showing a variation between 1.002 and 1.01, and two instances are cited to show the difference due to this cause.

“Taking the specific gravity of the dry slime as 2.66 and the weight of a litre of the wet pulp as 1260 grams (sp. gr. 1.26).

(а) If sp. gr. of solution = 1.0, then the percentage of dry slime = 33.07%.
(b) If sp. gr. of solution = 1.008, then the percentage of dry slime = 32.2.

Showing a percentage of difference of 2.63.
Again, taking sp. gr. of dry slime as 2.66 and the weight of one litre of the wet pulp as 1100 grams (sp. gr. 1.1).

(a) Taking the sp. gr. of the solution as 1, the percentage of dry slime = 14.56%.
(b) Taking the sp. gr. of the solution as 1.008, the percentage of dry slime = 13.47%.

The percentage of difference in this case would be 7.49.”

So, when the stock solution contains an unusually large quantity of soluble salts, thus raising its specific gravity considerably above that of water, the error due to this cause should not be over-looked. The above-named article gives the following table for ascertaining the correction to be made in each determination on account of the specific gravity of the solution in the pulp.

“Let the specific gravity of. the dry slime = 2.66; the weight of one litre of pulp = 1150 grams; the specific gravity of solution = 1.005. Required: The number of cubic feet of pulp to 1 ton of dry slime in the charge. In Table 9, at the intersection of the vertical column headed 2.66 and the horizontal column headed 1150, is found 133.3, the number of cubic feet of pulp to make one ton of dry slime when the specific gravity of the solution is 1. In the adjoining column opposite 133.3 is found 0.87, the number of cubic feet to be added to 133.3 for each increase of 0.001 in the specific gravity of the solution: 0.87 X 5 = 4.35 (total correction): 133.3 + 4.35 = 137.65 cu. ft. of the pulp specified necessary to make one ton of dry slime.”

Moisture Determination Preferred in Certain Cases

When a thick pulp is aerated by compressed air it often happens that the amount of air entrapped in the form of minute bubbles renders the Specific Gravity determination quite unreliable. By allowing the flask of pulp to stand for a few horns the level may fall from 1 to 2 inches, due to the escaping air, but a large proportion of the entrapped air will be held permanently thus increasing the volume to that extent. In such cases the only remedy seems to be to make a moisture determination by evaporation. It is not enough, however, to determine the relative weight of ore and moisture in a sample of given weight, because the contents of the tank are to be estimated by volume and that volume is occupied by a mixture of ore, moisture, and air, so the weight of pulp taken for the moisture sample should have its volume also determined in terms of cu. ft. in order that the weight of ore in a cubic foot may be accurately determined.

For instance:

1 Litre = 61.031 cu. inches or 0.03531 cu. ft.
1 Cu. ft. = 28.3174 litres
So if 1 litre of pulp be weighed and dried the weight of ore and water in a cu. ft. of capacity can be found.

Sampling Mill Feed Head and Plant Tailings

How to Sample Mill Feed Heads

This is the second of the more fertile causes of failure to check on bullion recovery. When milling in water the most reliable sample of ore heads is probably that taken from the pulp after it leaves the mortar boxes. This may be done by catching, a portion in a cup or other receptacle at regular intervals, and if care is taken that the whole depth and width of the stream issuing from the screens is included, that the cup is not allowed to overflow, and that the intervals are regularly timed and sufficiently frequent, the resulting sample is usually reliable.

A better way is to place an automatic sampler in the stream of pulp, thus eliminating the personal factor, but great care is necessary to see that the sampler used is correctly designed to cut a perfect section of the stream both in breadth and depth, because a stream of pulp flowing in a launder is not homogenous, and moreover the effect of a slight error in the product of a mechanical sampler is cumulative, that is, it is invariably in the same direction and is not subject to the correction which may automatically occur in other circumstances where errors in excess and defect may neutralize one another over a period and result in a representative average reading.

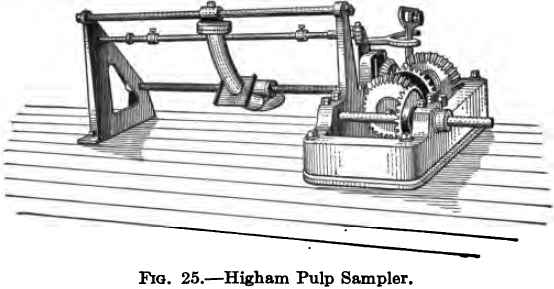
An automatic sampler that satisfactorily withstood very severe and searching tests on the Rand is that invented by James Higham and described by him in the Journal of the Chem., Metall. & Min. Soc. of S. A.

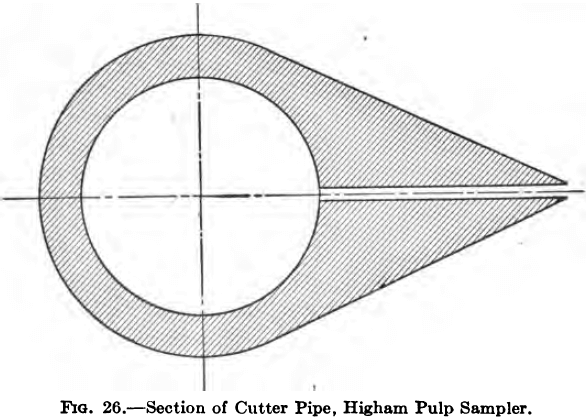
It will be seen from the illustration that it is essentially a short length of curved and slotted pipe that is made to pass across the stream of pulp by means of the screw mechanism which is power

driven, and the direction of travel automatically reversible. A break is made in the pulp launder and the stream in dropping from

the upper to the lower level encounters the slotted pipe which cuts out a section of it and delivers it to a suitable receptacle placed underneath. The normal size of sample taken is about 2000 lb. per day from a 100 stamp mill, or 1 ton from a daily tonnage of presumably about 1000 tons of ore.

The only objection raised to this sampler has been the unwieldy size of the resulting sample but this may be obviated by inserting a second sampler below the first to reduce the quantity taken to convenient dimensions, or by the use of the Higham Dividing Box, a trough fitted with a number of knife edged slots, at right angles to it, acting on the same principle as the Jones dry ore sampler. The trough is placed parallel with the direction of movement of the sampling pipe and as the outflowing pulp passes over the slots a definite proportion of the stream enters and is received in a second trough underneath, the remainder or reject flowing away to join the main stream. Any machine, however, will answer the purpose that is so designed as to cut a perfect section of the stream both horizontally and vertically without appreciable acceleration during any part of the stroke, and with a minimum of splash and diversion of the line of flow.

When milling in cyanide solution it is difficult to obtain a head assay from the pulp owing to part of the gold passing rapidly into solution. Methods have been suggested on the Rand and are said to have been carried out with a certain measure of success, whereby the true value of a pulp sample taken under these conditions is calculated by ascertaining the ratio of solution to ore in the sample, and the assay value of the solution before entering the mill and also as present in the pulp, and then adding on to the assay of the ore the equivalent of the gold dissolved during milling as shown by the solution assay. This method, while it seems theoretically capable of giving correct results, yet is open to so many possibilities of error and needs so much care and time expended on it that it hardly commends itself as a practicable everyday solution of the problem.

The only alternative is to sample the ore before it comes in contact with the solution, and if properly done, this method may be made to yield reliable working results. It is possible to set about it in two ways, first, to install a complete sampling plant in the mill, cutting out a section of the stream of broken ore going to the bin and subdividing it by machines interspersed with crushing devices for reducing the size of the particles after each quartering until a small but representative assay sample remains. This, while satisfactory, is costly, both to install and to run, and some important mills which adopted the system have since abandoned it as not yielding any adequate compensation for the expense involved.

The second method is to cut out small individual samples of the ore periodically at some point after it leaves the breakers. If means can be found to do this regularly and fairly, a good representative sample may be obtained. The most reliable system is of course an automatic sampler if it is practicable to insert one somewhere between the rock breaker and the intake of the mortar box, but hand samples faithfully and regularly taken are on the average dependable. An important point to be observed is that as long as the ore is coarsely broken, the aggregate sample for the day or shift must be a large one or it will be of no use. When cutting out, at regular intervals of half an hour, samples of a two-inch rockbreaker product in a mill crushing 100 tons a day, an aggregate sample of 1000 lb. for the twenty- four hours is not any too much, and 2000 lb. would be safer. This should then be all crushed to about ¼ inch size before being quartered down to a smaller bulk. The mixing and quartering may be done by hand shovelling or one of the various mechanical devices may be used. When the bulk is reduced to about 100 lb. this should then be crushed to pass 1/8 inch screen and quartering continued till the sample weighs about 20 lb. when it should be ground to pass 10 mesh; in this condition it may be reduced in bulk to one or two pounds and then sent to the assay office where the process is continued until the necessary assay sample of 80 or 100 mesh is obtained. This may seem an un-necessarily expensive and laborious process, but it cannot be shortened with safety if the resulting assays are expected to furnish a basis on which to figure bullion returns.

An unusually significant example of this contention, drawn from the writer’s own experience, is here given by way of illustration. The ore in question was a gold-silver ore in which the gold, more especially, occurred in a notoriously “spotted” manner. The assays given are combined gold and silver results. The sample for the twenty-four hours was taken by hand from the battery feeder, a portion being caught every hour in a specially shaped scoop as it fell off the edge of the disc. The total weight was about 200 lb. and maximum size of particles from one to one and a half inches. In the course of an investigation into a continued and serious shortage of bullion as compared with the amount expected from a consideration of head and tail assays, a special series of tests was made on the method of quartering down the daily ore head sample.
Each day’s sample for a number of days in succession was either mixed and quartered direct or the whole was crushed to pass ¼-in. mesh before mixing and quartering. Duplicate samples were made at the first coning-up and quartered down and assayed separately, forming checks on the method of quartering. The results are summarized below.

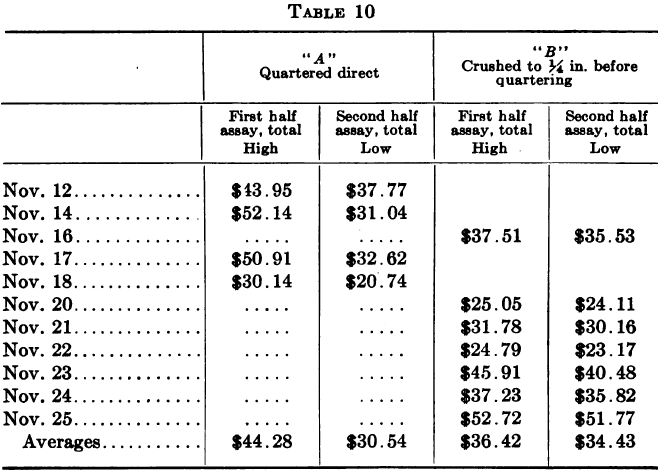
The above indicates a possible error of about $14 a ton when the original sample is not crushed fine before quartering, while in the other case the difference shown is only $2.00.

It may be asked, in regard to “A,” why the error shown should be supposed to account for a uniformly high result in the long run, instead of neutralizing itself over a long period of time, and it should be noted in reply that the source of the error is not likely to operate on the side of defect, or only to a slight extent, for this reason: since it is known that the ore is spotted in value and that a small stone may assay several hundreds of dollars right along¬side of quite low-grade rock, let us suppose that a certain battery sample is fairly uniform but contains one stone of “high-grade” value; if, in coning and quartering the sample, that stone happens to be in the rejected quarter, the sample taken for assay will be representative, whereas if it happens to fall in the quarter saved the assay sample will be thrown up to the high limit of error shown. Thus, it is not so much a question between excess and defect (neutralizing one another) as it is between excess and mean, yielding an average in excess, over a period.

It is obvious that the greater the number of pieces into which that stone of “high-grade” is broken before the sample is quartered, the better the chance of its being distributed equally between the portion rejected and the portion saved, but on the other hand assuming the sample to have been broken sufficiently fine for safety at this stage, in continuing to quarter down this same sample the original danger appears again and increases in proportion as the sample gets smaller so that it will soon become necessary to subdivide the particles still further in order to obtain an even distribution of the high-grade ore throughout the mass.

A. Harvey gives the following table as a guide to the margin of safety in size of ore pieces.

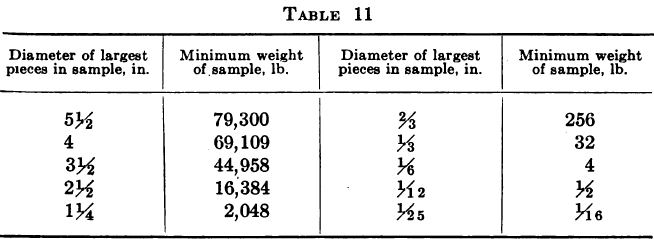
These methods of sampling the heads are necessarily expensive and as it is not always easy to point to any material gain in monthly profits resulting from their adoption, and as moreover, their use does not invariably result in the establishment of an accountant’s balance between the bullion debited and credited to the mill, many companies have asked themselves whether they were not wasting time and money in trying to ascertain the true value of their ore heads and have finally decided to be content with a nominal value for the ore, obtained by adding the amount of bullion actually recovered to the aggregate amount of gold going to the dump in residues and dividing the sum of these by the tonnage for the month. The degree of satisfaction to be derived from this solution of the difficulty is a matter of individual opinion, and while admitting that it is not possible to ascertain head and tail assay values and tonnage with sufficient accuracy to furnish a check on small losses through carelessness or petty pilfering, yet the present writer confesses to a preference for making the best attempt possible to ascertain the real figures in each case, so as to act as a check against serious losses and afford an indication of any radical defects in the operation of the plant.

How to Sample Plant Tailings Residues

This is comparatively easy as the pulp at this stage is finely comminuted and usually homogeneous, so that only ordinary care and common sense should be needed to obtain a reliable sample.

In the case of sand the charge may be bored from top to bottom in a number of places after having leached dry preparatory to discharging, or if the residue be discharged into trucks each load may be bored as it passes to the dump. In boring a tank charge care should be taken when using the ordinary split tube sampler not to take too much at a time, since if the rod be worked down from top to bottom without being withdrawn and emptied there is danger that the lower strata may escape sampling. It is better to drive down about 12 inches, then withdraw and empty the pipe, and then after carefully inserting in the hole without breaking down the sides, sample the next 12 inches and so on to the bottom. If on account of the method of filling or any other reason it seems probable that the charge is not homogeneous it is better to divide the area of the tank into concentric rings containing an equal tonnage and bore in each ring an equal number of holes so that the quantity of sand taken from each ring will be representative of the tonnage contained therein.

For slime residues the use of the automatic sampler is probably the most satisfactory method where the pulp is discharged in a homogeneous fluid condition.

The sample of filter cake is not so easy to obtain. One method is to cut a section Of the cake from a leaf of each charge or in the case of the rotary filters to take a grab sample from the scraper periodically. It sometimes happens, however, that a sample dipped out of the discharge launder as the watery cake is flowing to the dam does not give an assay check on the sample cut from the cake before discharging, the latter being usually lower. The reason for this is probably that, assuming the sample taken from the launder to be a correct average, there may be with almost any type of filter a loss of a small amount of valuable solution which passes out with the cake and in that case the sample taken from the leaf does not represent the whole of the lost metal going to the dams.

Sampling Pulp at Different Stages of the Gold Leaching Circuit

If this is to be of any value at all it is absolutely necessary that the action of the cyanide on the ore should be stopped immediately the sample is taken. This may be ensured in two ways:

1. A sample taken every hour, for instance, at a certain point in the treatment may be at once placed on a laboratory vacuum filter and filtered and water washed, the several cakes composing the twenty-four hour sample being dried, mixed, and quartered down for assay as one sample;
2. or a method devised by H. A. White may be used. The sample as soon as taken is placed in an enamelled bucket and enough saturated solution of potassium permanganate added to maintain a permanent pink coloration in the solution during the whole period of sampling. This destroys the free cyanide and stops further action on the ore.

At the end of the period of sampling, usually twenty-four hours, the contents of the bucket are well mixed, washed by decantation or filtration and sent for assay. The reaction between the permanganate and the cyanide takes place without precipitation of the gold but whether this is true of the silver content of the solution the writer has never determined as he has been accustomed to use the immediate filtration and washing method.

Discrepancy in Assay of Leach Circuit Tailings

In the case of gold ores there is a possible source of error in the assays which will tend to show a higher extraction than has actually taken place, and therefore an apparent shortage of gold in the clean-up. W. A. Caldecott has shown that when a sample of slime containing potassium auro-cyanide solution as moisture is dried for assay it is almost impossible in the subsequent fusion to collect in the lead button all the gold present in this form probably on account of its being deposited in such minute particles as to approach the molecular state, there being therefore not enough globules of reduced lead to come in contact with every molecule of gold. It was found that the finer the litharge in the flux was ground the higher was the resulting assay in gold, but that under the most favorable conditions the gold content found was lower than that obtained by washing the pulp thoroughly and assaying the ore and washings separately. Whether the above reason be the correct one or whether the loss of gold be due, as is maintained by some assayers, to a deposition of the gold bearing solution on the walls of the vessel used for drying the sample, the fact of the discrepancy has been well attested and it was probably in consequence of this investigation that the Rand practice was developed of “fixing” or precipitating the gold in the slime residues by the copper sulphate method used for solution assays before drying the pulp.

A. Whitby states that his practice is to add to the slime residue first a little cyanide solution and then small quantities of solutions of copper sulphate, sodium sulphite and sulphuric acid. After mixing thoroughly the pulp is turned out into an enamelled dish and dried, care being taken to avoid spitting. The sample is then passed through a 100-mesh screen and assayed. It is the custom on the Rand to take exceptionally large charges for the assay and for low-grade pulps it is a necessary precaution especially where a large mill tonnage will multiply an error of a few cents in the assay to a serious sum total of gold in the month’s tonnage. From five to ten assay tons of pulp are usually taken for an assay of residue, distributed over two or more crucibles. The flux used by Mr. Whitby for the Rand residues has the following proportions:

Ore………………………………………………………5 A.T.
Litharge……………………………………………….4 A.T.
Sodium carbonate…………………………………5 A.T.
Borax…………………………………………………..1 A.T.
Reducer, sufficient to give a button of about 45 grams.

That the error due to neglect of these precautions may be serious is shown by an experience of the writer with a high-grade gold-silver ore in Mexico. It had been the custom to estimate the assay of ore passing to the cyanide plant by assaying the pulp as thickened in the cyanide solution, prior to agitation, the argument being that as no part of the mill solution was withdrawn for precipitation the amount of gold and silver circulating in that medium might be taken as fairly constant and that therefore an assay of the thickened pulp with its normal burden of dissolved gold and silver would truly represent the value of the pulp leaving the mill, and this value plus that contained in the concentrate would represent the assay of the mill head ore. In practice, however, there was a persistent plus recovery of gold over that shown by assays.

On precipitating the pulp before drying for assay it was found that the gold value as shown by the usual method was much too low though the silver did not appear to be affected. A comparison run daily for 26 days with and without preliminary “ fixation” of the gold showed an average gain in the assay of $1.40 per ton due to “fixation,” the figures being $13.90 by the usual method and $15.31 by the preliminary “fixation.” Of course this is an extreme instance, but in the case of residues a persistent error in the assay of only 10 c. a ton on the low side would make a serious difference between actual and theoretical recovery.