The concentrator of Bonneville Ltd. at Wendover, Utah, processes a feed obtained by solar evaporation of a brine containing sodium and potassium chlorides with minor amounts of impurities. Salable potassium chloride concentrate is produced from this feed in two steps: flotation with amine reagents to concentrate the potassium chloride, and washing of the concentrate with fresh water to reach final grade. In the flotation step emphasis is placed on recovery, whereas the washing step has as its objective the production of salable grade (in excess of 60 percent K2O equivalent), with recovery being important but secondary.
If the process is arbitrarily divided into flotation and washing functions, there are a number of variables involved. Among those for flotation are:

while washing includes:

The over-all objective of this study was to utilize statistical techniques to achieve better understanding and control of the flotation operations. Only flotation recovery was considered. A separate study is being made on washing.
The data used in this study are from 276 consecutive shifts. The data were recorded once per shift and are assumed to be accurate; that is, no allowance for assay or other errors was made.
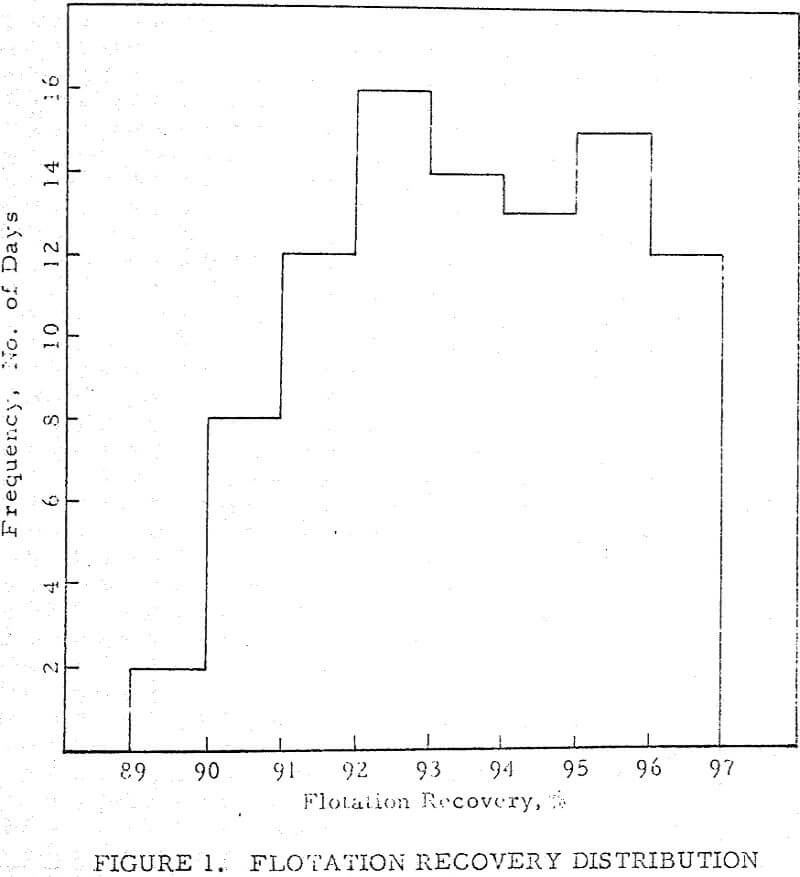
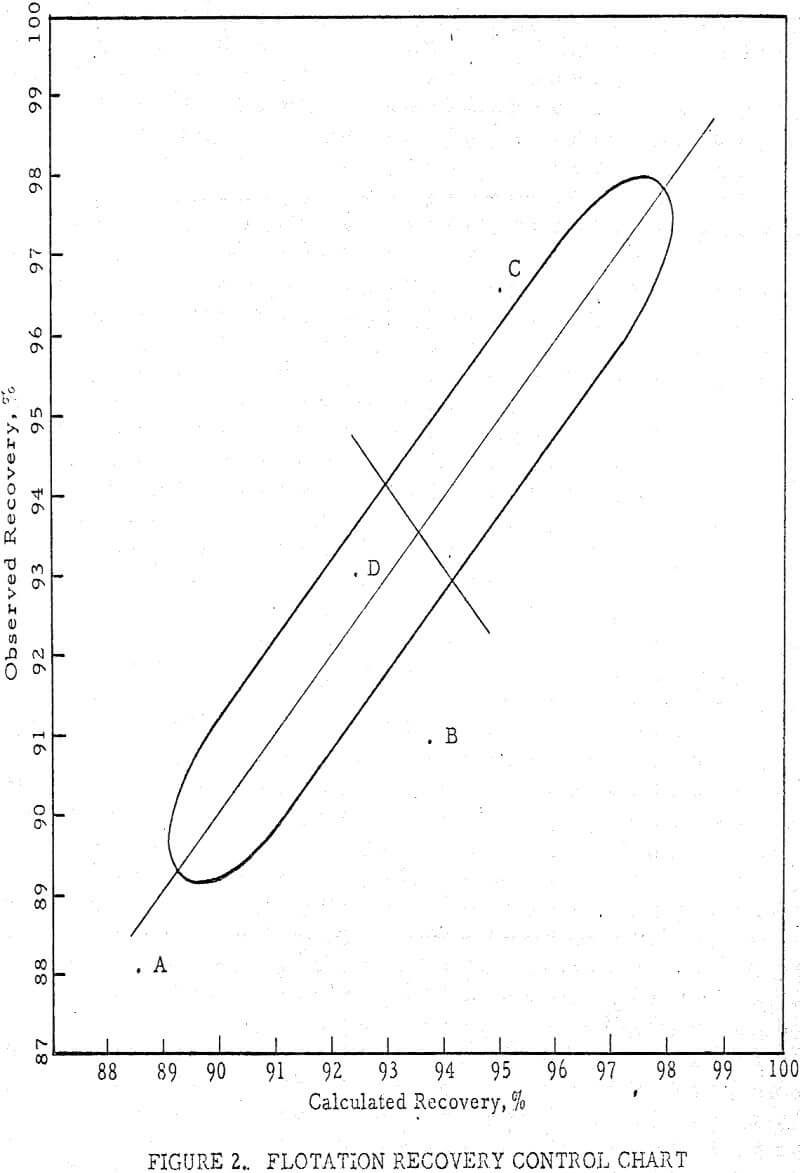
The sigma limits referred to are often useful as action limits, for they define a field of known probability within which observations should fall if chance causes alone are operative. At best, if the distribution is normal, it is 99.7 percent probable that an observation will fall within three sigma limits, and approximately 95 percent probable that it will fall within two sigma limits.
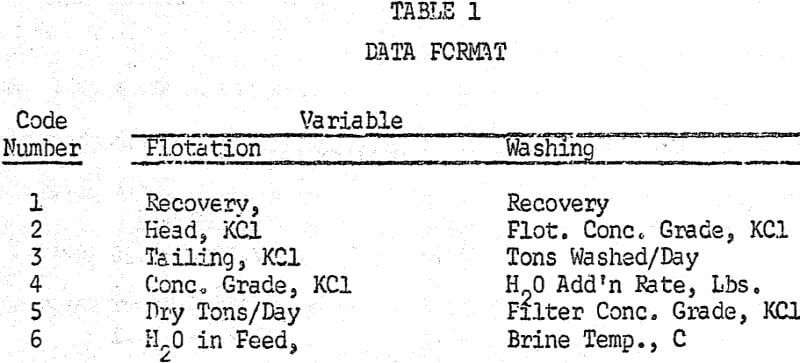
Table 2 lists the means and standard deviations of the variables.
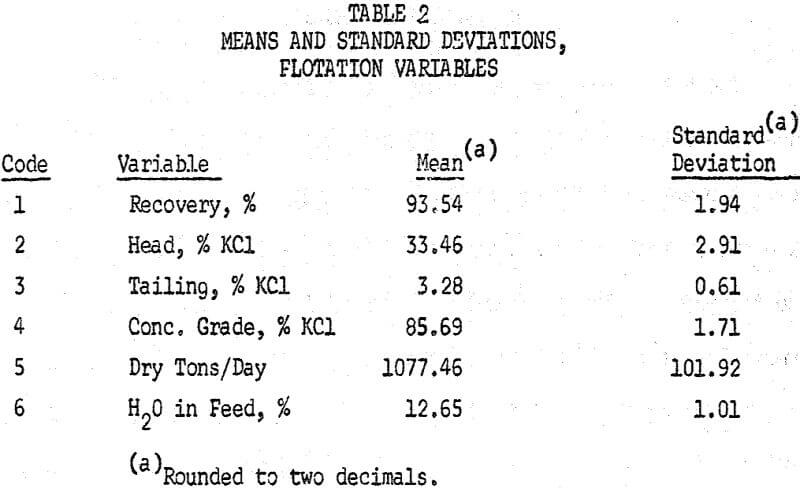
The significance of these numbers is best seen by listing the three sigma limits, or the limits within which a given value should fall 99.7 percent of the time, as in Table 3.
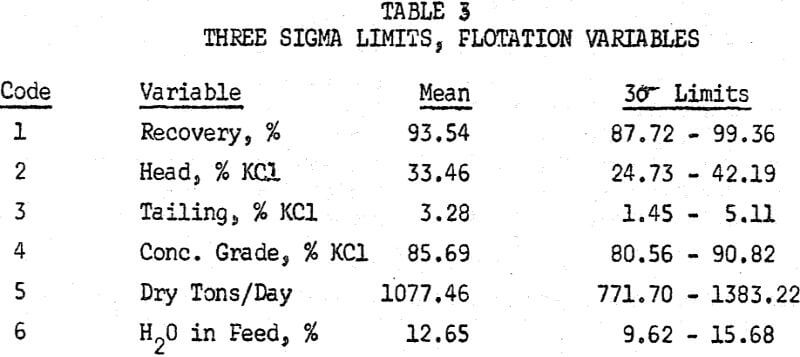
The ranges do not imply that readings will be obtained very often rear their outer limits, especially if some physical factor is functioning as a control. For example, it is quite unlikely that a recovery of 99.36 percent would ever be obtained, due to the physical limitations inherent in flotation. On the other hand, a recovery as low as 87.72 percent is easily attainable, but the improbability of its occurrence would indicate some failure in the process if recovery fell below this figure. .
The regression equation for recovery in terms of the other variables was found to be:
Y = 93.85 + 0.34817 X1 – 1.7976 X2 – 0.069036 X3 – 0.00039366 X4 + 0.022256 X5
Where: Y = recovery, %
X1 = head grade, % HCl
X2 = tail grade, % KCl
X3 = conc. grade, % KCl
X4 = dry tons/day
X5 = moisture, %
Since this equation contains terms for head grade, tail grade and concentrate grade, at least one of these variables is not strictly independent, because recovery can be calculated from knowledge of these three grades. Consequently, the high degree of correlation for equation (3) could be quite misleading.
To make this equation meaningful, at least one of the independent variables must be eliminated. The regression equation was redetermined with head grade, tailing grade, and concentrate grade eliminated in turn. Of the three new regression equations, the one with concentrate grade eliminated was especially interesting. The concentrate is a high-grade product and is difficult to assay by rapid instrumental methods. The possibility, therefore, of predicting recovery from rapid analyses of the low-grade products (head and tailing) which could facilitate mill control, is enhanced by elimination of concentrate grade as a variable.
The final equation is:
Y = 87.21 + 0.3588 X1 – 1.8547 X2 – 0.00024 X4 + 0.05299 X5…………………………(4)
The multiple correlation coefficient is 0.96995. The other multiple correlation coefficients with tailing grade eliminated and head grade eliminated are respectively 0.78383 and 0.82088.