Table of Contents
The stress distribution around single and multiple underground openings has been determined both from theory and from photoelastic laboratory model studies. These determinations require certain simplifying assumptions: The rock is elastic homogeneous, and isotropic; the opening or openings are in an infinite medium, are subjected to plane stress or strain, and are not affected by boundary conditions the stress field is symmetrical; and the opening can be represented by simple geometric shapes, such as circles, ovaloids, and ellipses.
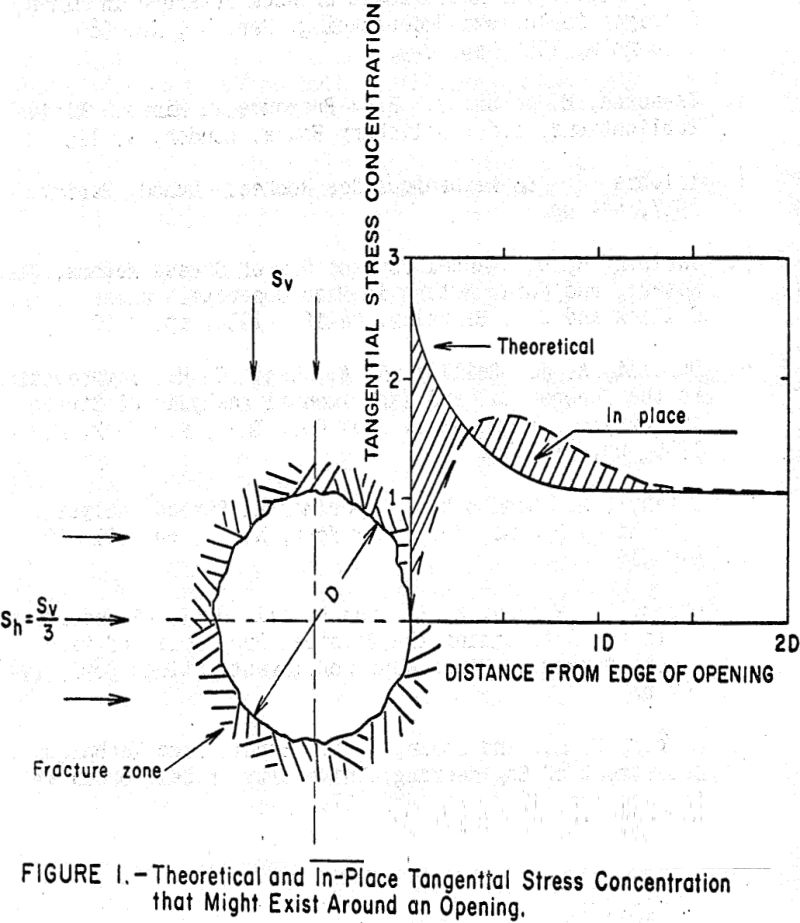
The question can be asked: Just how well do these assumed conditions fit the actual underground conditions in operating mines? For example, consider a circular opening when horizontal stress in a biaxial stress field is equal to one-third of the vertical stress. Theoretically, the maximum stress concentration is tangent to the skin of the opening. The sides of the opening (at the ends of the horizontal diameter) are subjected to a compressive stress concentration equal to 2.67 times the average stress in the undisturbed rock, and the tops and bottoms (at the ends of the vertical diameter) of the opening are under zero stress concentrations. Furthermore, the stress concentration decreases as the distance from the opening increases. For practical purposes, the stress concentration at a distance twice the diameter from the skin of the opening is equal to one; that is, the stress in the rock is the same as if the opening were not there. In this report, that distance is called the “limit of the zone of influence.”
Contrary to theory, underground measurements show that in many instances the maximum tangential stresses are not concentrated on the periphery of the opening but are some distance in from the edge. This concentration has been attributed to the blasting fractures in the skin of the rock, which part relieve the stress, or to the inelastic behavior of the rock. In either instance, this part “de-stressed zone” can have the effect of enlarging the “zone of influence” of the opening.
Figure 1 shows the tangential stress concentration around a circular opening as computed from theory and as might exist under in-place conditions in a mine.
It follows that when two openings are less than two diameters apart, the “zone of influence” around one opening affect the “zone of influence” around the other. For the type of stress field cited in the preceding example, the stress concentrations on the adjoining sides of two circular openings that are one diameter apart and on the same level would be increased from 2.67 to 3.2 times the average stress. The tangential stress concentration on the top and bottom of the openings is increased only slightly above the zero stress concentration that existed for one opening.
If the two openings are not on the same level but are one above the other, then the upper opening has the effect of shielding the lower opening from a part of the stresses resulting from the vertical load.
This effect, in turn, changes the stress concentrations owing to the lateral stresses. For example, consider that when all the vertical stress is removed from the lower opening, the opening is subjected to only the lateral stress. For the type of stress field as shown in figure 1 the sides of the opening would have a tensile stress concentration equal to one-third the average stress, and the top and bottom of the opening would be under compressive stresses equal to the average stress.
One of the primary results of the investigations briefly discussed in this report is the agreement between the foregoing theoretical considerations and the in-place measurements in operating mines. A block caving stope was believed to affect an adjacent mine opening in the manner described if the size of the opening were small in comparison with the size of the stope, if the void created by the undercut would shield the underlying drift from the vertical stress field and if the assumed and in-place original stress conditions were similar. Some of the Experimental procedures and results of these investigations are described, and their application to mining problems is discussed.
Experimental Procedure and Results
A series of experiments were planned to investigate the changes in stress around mine openings in operating block caving mines. Mines and test areas were selected to provide mine openings of different sizes and shapes, diverse mine layouts and mining sequences and rocks that ranged from hard to soft.
Changes in strain and of deformation in slusher drifts and grizzly drifts were measured to obtain estimates of the stress concentrations in the rock surrounding the drifts and in the concrete linings that normally are used for support. A brief description of some of the instruments, test procedures, and preliminary results of the tests follow.
Instruments
The changes in radial strains in the rock surrounding slusher drifts were measured with electrical wire resistance strain gages (Carlson strain meters). The principle of this gage is that the change in electrical resistance of an elastic steel wire is proportional to the change in tension of the wire and that the tension in the wire changes in proportion to changes in strain in the medium (rock), in which the gage is properly embedded. The minute resistance changes in the gage are measured with a modified wheatstone bridge circuit.
The changes in tangential strains on the surface of the concrete lining in the slusher drifts were measured with a mechanical strain gage (the Whittemore gage). This gage measured the displacements of measurement points attached to the concrete directly with a micrometer dial indicator.
The stress-strain properties of the rock and concrete were determined by standardized laboratory test methods. The values of these constants and the values of the measured strains were entered in standard equations to obtain estimates of the stress concentrations. The derivation of these equations is described in other publications.
The changes in the vertical dimensions of the slusher drifts (deformation) were measured with an extensometer designed and built by one of the mining companies cooperating with the Bureau of Mines in rock mechanics studies.
The extensometer is essentially a long mechanical scale that is used to measure the vertical distance between two measurement points, one of which is in the back and one in the floor of the drift.
Several hundred of these measurement points were installed in the drifts by the mining company, whose engineers take daily measurements.
Procedure
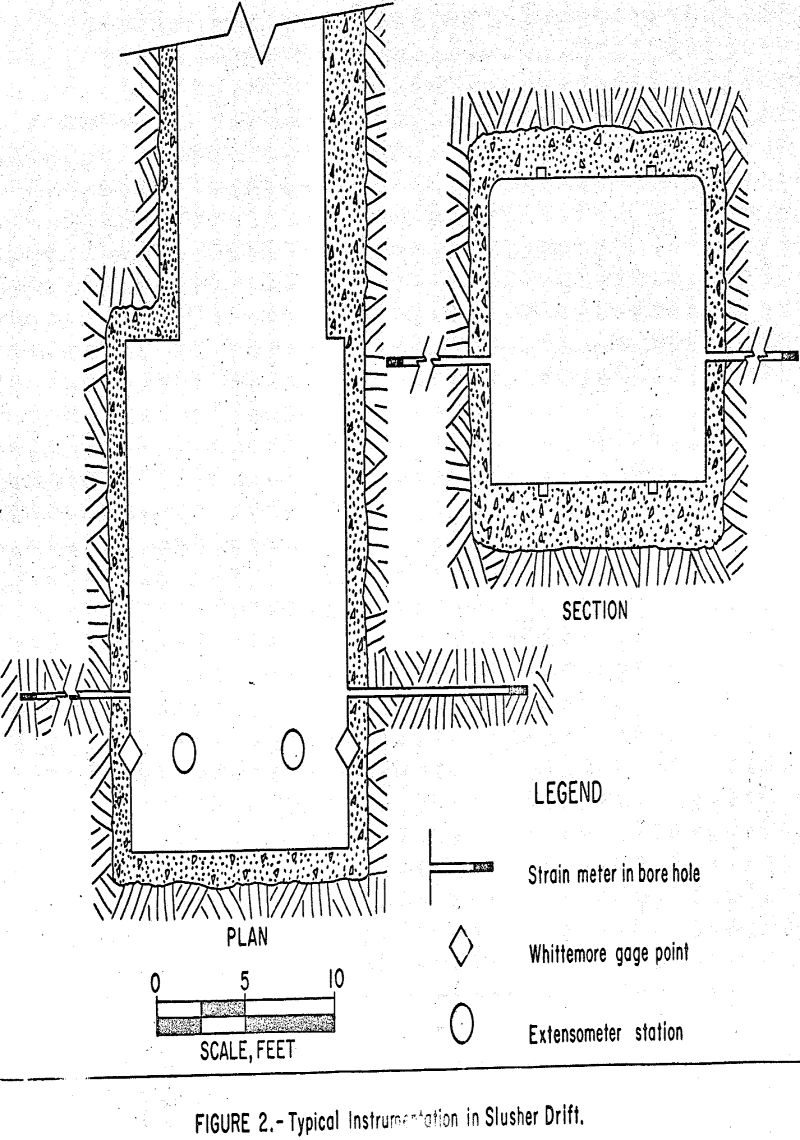
The strain meters were grouted in diamond-drill holes drilled in the sides of the drifts. The Whittemore measurement points were attached to the surface of the concrete lining in the drifts. The vertical extensometer measurement points were also installed near the surface of the concrete lining. Figure 2 shows a plan and section of a typical installation in a slusher drift.
Measurements were taken before, during, and after undercutting in the block caving stope above the slusher drifts. Cracking, spalling, and other visible signs of stress concentrations were also noted. A photograph of an engineer taking a measurement with the Whittemore gage is shewn in Figure 3. Figure 4 is a photograph of an engineer-taking a deformation measurement. A photograph of typical tension cracks is shown in Figure 5.
Test Results
The values of the measured strains and the average elastic constants of the rock or concrete were used in computations for estimating the changes in the stress concentrations.
Examples of test results from each of the three different types of measuring instruments follow. Similar results, not included in this report, were obtained from other instrument stations.
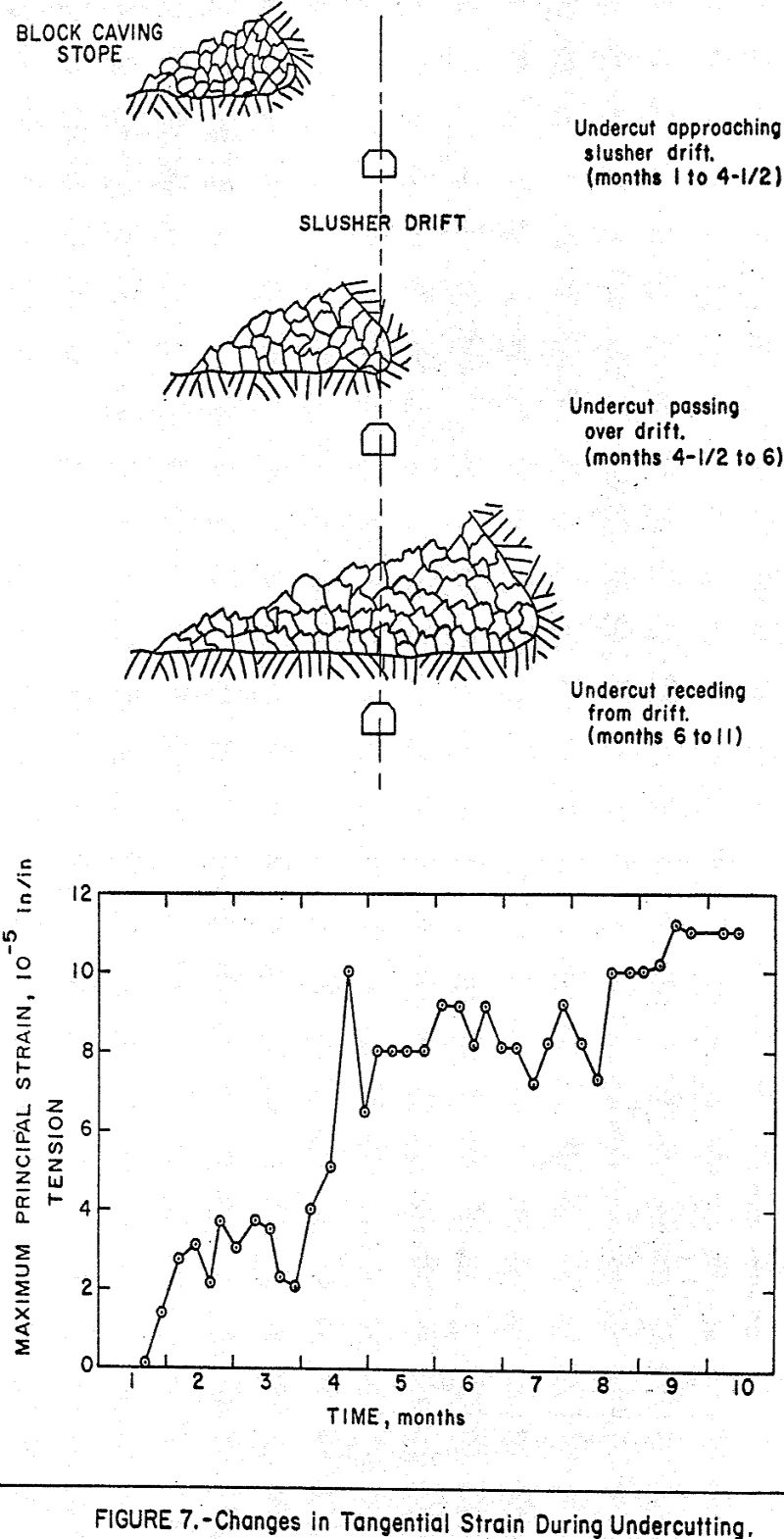
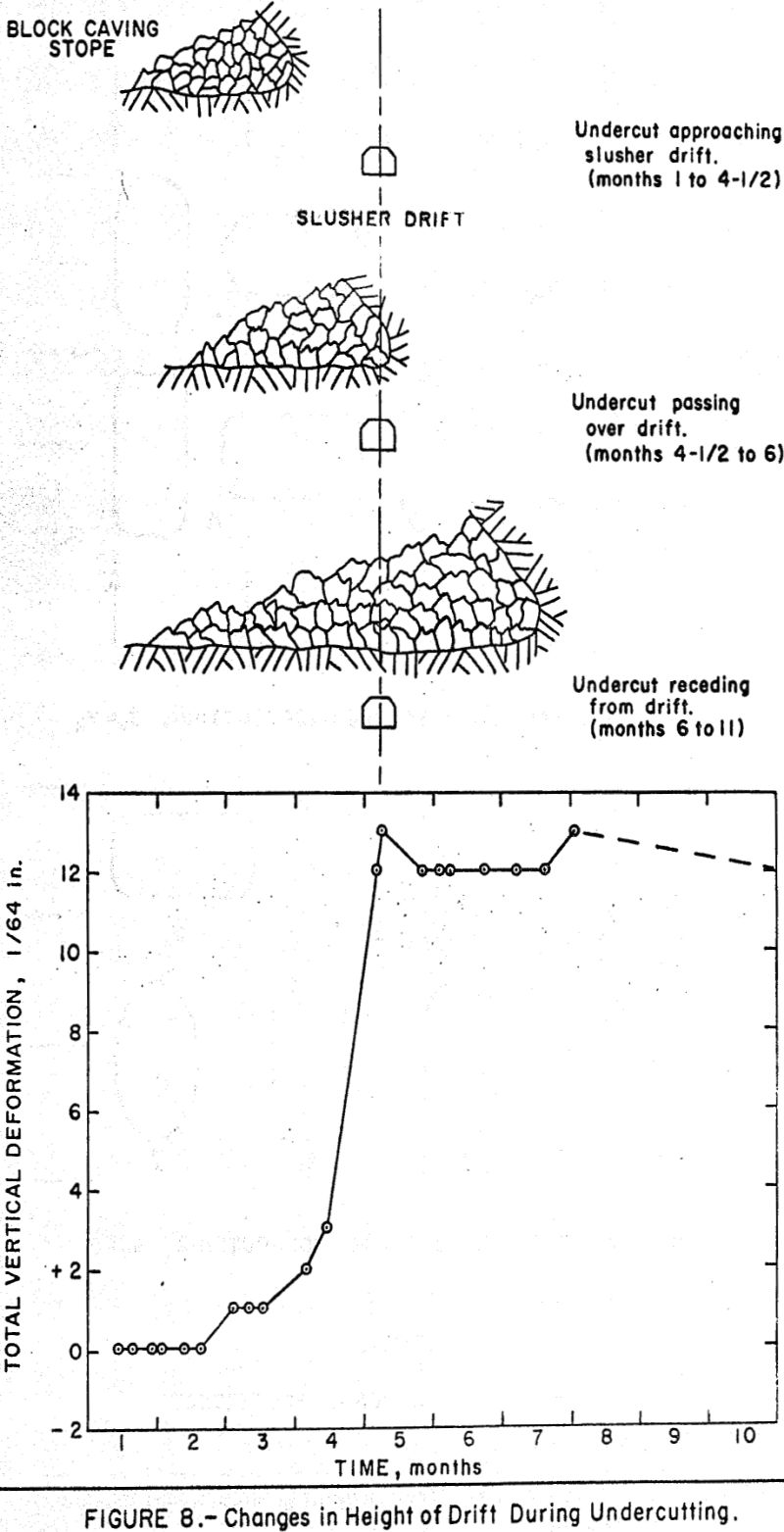
The results of a radial strain measurement are shown in Figure 6 where the changes in strain are plotted as a function of time. The positions of the undercut with respect to the slusher drift are also shown in a simplified cross section.
The radial compressive strain in the rock increased about 750 milllonths of an inch per inch (microinches per inch) as the undercut approached the slusher drift and decreased as the undercut passed over the drift. This increase in strain represents an estimated increase in stress of 2,500 p.s.i. Note also that the measured change in strain continued to decrease as the undercut progressed beyond the drift.
The decrease in strain leveled off 6 months later when the undercut had advanced 365 feet beyond the instrumented slusher drift. Because the magnitude of the stress in the rock before mining was unknown, the magnitude of the change in strain is plotted as recorded by the instrument. In the example of radial strain depicted in Figure 6, a portion of the decrease in compressive strain is recorded as tensile strain. However, since it can be assumed that the rock before mining was under both a horizontal stress and a vertical stress, the tensile strain is in reality a decrease in the original compressive stress.
The results of a tangential strain measurement are shown in Figure 7. The maximum principal strain increased about 80 micro-inches per inch in tension during the same period of undercutting. This represents an estimated increase in tensile stress of 250 p.s.i. Note that the maximum principal strain is a value computed from strains measured in three different directions. During the period of measurement, the direction of the maximum principal strain rotated about 90 degrees as the undercut passed over the station.
The results of a deformation measurement are shown in figure 8 where the changes in height (deformation) are plotted as a function of time. Note that the vertical dimension of the drift increased about 11/64 of an inch as the undercut passed directly over the measurement station.
Discussion
General agreement is noted between the measured changes in the tangential and radial stresses and the stresses computed from theory. As the undercut progressed over the drift, the maximum principal stresses on the sides of the drift increased in tension, and the horizontal radial stresses at a distance of about one diameter away from the edge of the drift decreased in compression. These changes indicate that the vertical compressive load on the drift was relieved by creating space (undercutting) above the drift.
When noting these agreements, it is important to recall the location of the instrumentation with respect to the mine opening. In the foregoing examples, the radial strain was measured at a distance of 3 radii from the center of the drift, that is, one diameter from the edge (see Figures 1 and 2). Theoretically, the radial stress concentration at that location is less than one-half the applied vertical stress (biaxial stress field in which the horizontal stress is one-third the vertical stress). Therefore, the stress concentration induced by the mine opening (before under-cutting) has the effect of only slightly increasing the radial stress existing in the undisturbed rock at that location. For practical purposes, then, the measured changes in strain at that point can be attributed mostly to the changes in the stress field induced by the undercut. The maximum tangential strain was computed from strain measurements on the surface of the mine opening. As shown in Figure 1, this location is at the point of suspected maximum stress concentration as theoretically computed. Hence, these measured changes in strain can be attributed to changes in the stress concentrations, which occur when the original vertical load on the opening is partly or wholly relieved by the undercut. Because divergence between the back and the floor of the drift was measured vertically at points about one-fourth the diameter in from each edge of the drift, any change in the vertical dimension of the opening would be caused by changes in the applied stress.
Therefore, it can be concluded from the in-place measurements that a decrease in radial compressive strain accompanied by an increased tangential strain and divergence of the opening could occur if the vertical stress were decreased. Furthermore, theoretical computations which treat the slusher drift as a circular opening in a plane biaxial stress field, show that when strains were created as recorded underground, the vertical component of the stress field was almost completely removed by the undercut. Future investigations are planned to obtain a more precise, numerical evaluation of the stress relieve by undercutting and of the agreement between assumed conditions and existing theory.
Because the different types of measurements generally agreed and because results obtained in test areas in different mines at different locations were similar, these data are believed to represents reasonably good estimate of the stress, changes that occur around mine openings beneath a block caving stope.
Application to Mining Problems
This question presents itself; How can the results of these preliminary investigations be applied to problems of rock pressure on mine workings beneath block caving stopes? Some of the several logical approaches are more promising (1) Reduce the stress concentrations by selecting the most favorable shape of opening; (2) increase the strength of the supporting structure by developing a design that takes into consideration the stresses to which the structure will be subjected; and (3) reduce the changes in stress by planning the mining sequence. The following examples illustrate some of the many approaches to the best solution of the specific problem in the mining industry.
The shaped opening that induces the lowest stress concentration will be the most favorable. In practice, the shape and the size of the slusher drift or grizzly drift will also be governed by plans for produced tonnage, the size of the broken ore from the stope, and the type of mining equipment to be used.
For minimum stress concentrations the design of the opening will depend upon the types of stress fields in the rock surrounding the opening.
Information concerning the stress field in the undisturbed rock, in the rock after the opening is driven, and in the rock after the undercut is mined can be obtained by measurements and to a lesser degree by visual observations and from theory.
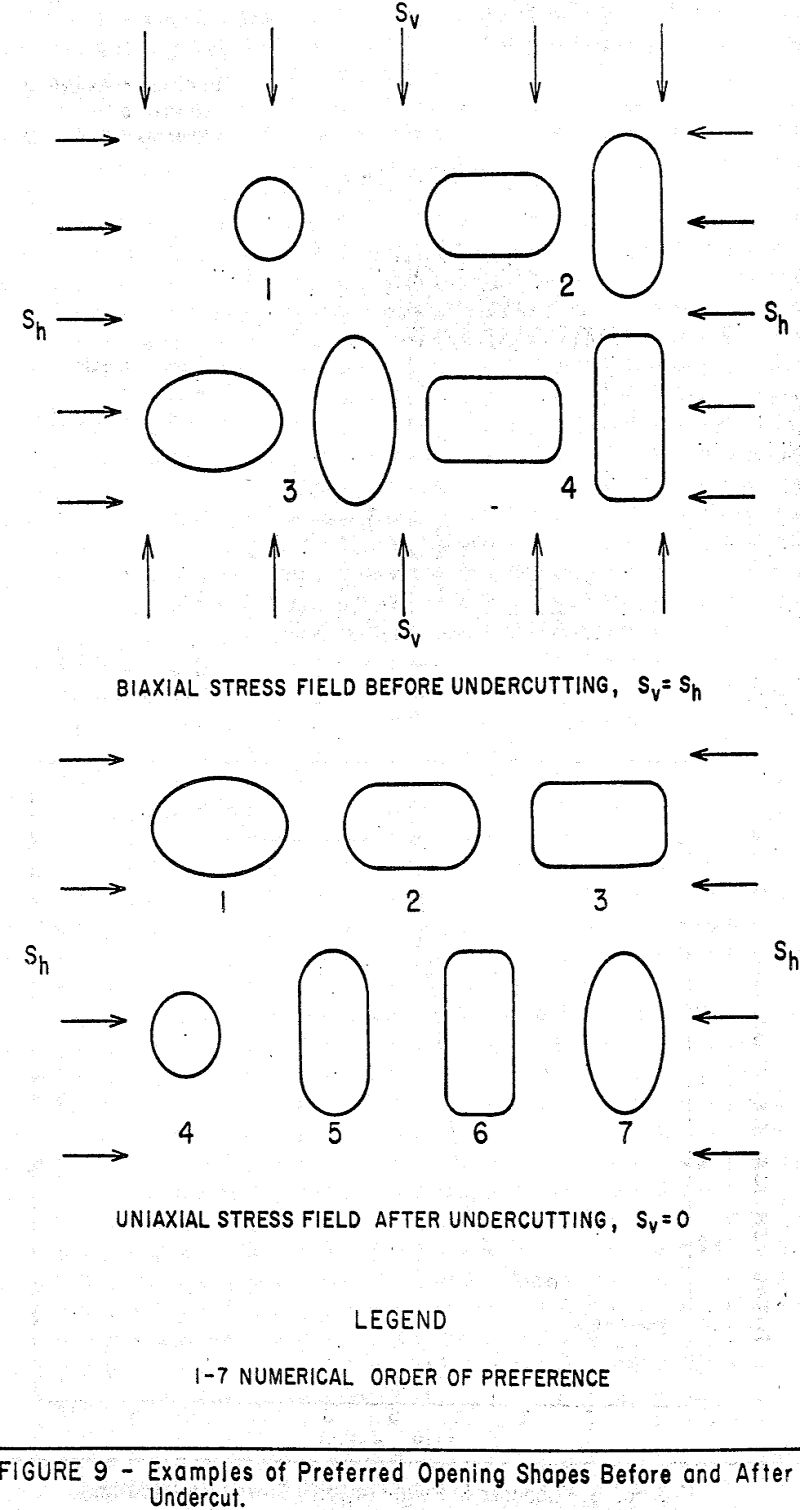
The approach to the most favorably shaped openings, for block caving mining, is illustrated by the following example selected: Consider a mine opening in a uniform, biaxial (hydrostatic) stress, field where the vertical and the horizontal stresses are equal. For simplicity, also consider only openings with regular, geometric shapes such as circles, ovaloids, ellipses, and rectangles with rounded corners. Which shape of opening would be the most favorable?
Before undercutting, the opening would be subject to a hydrostatic stress field. Hence, a circular shape would be the most favorable. Because immediately after undercutting, the opening would be in a uniaxial stress field, an elliptical opening with a height-to-width ratio of 0.5 would be more favorable. The second preference both before and after undercutting is an ovaloidal opening. Apparently under the described conditions the best compromise would be an ovaloidal opening. The types of openings are discussed and their numerical order of preference before and after undercutting are shown in Figure 9. The preferred opening sizes and shapes in the specific example presented were based on assumptions concerning the stress field and the rock properties that may or may not be applicable for a specific mine.
Logical, approaches to the design of the supporting structure should also be based upon knowledge of the stresses to which it will be subjected. Consider, for example, the installation of concrete supports before the undercutting operation. The tensile strength of concrete is low. Yet the structure will be loaded in both tension and compression during the different stages of mining. Hence, methods of civil engineering design for structures stressed in tension should be investigated. These include, among others, high strength concretes, prestressed concrete designs, reinforced concrete, and expansion joints that allow the structure to adjust to tensile stresses.
Another approach would be to install temporary supports such as roof bolts, timber sets, or steel supports, during the first development and undercutting operations. Later, after the major stress changes had occurred, permanent concrete linings could be placed.
From stress changes as predicted from theory and as measured underground, possible remedial measures are also suggested for reducing tensile stresses by driving the opening in “de-stressed rock” after undercutting. Although this procedure could increase the initial cost of development and might influence caving the ore, cases are possible when such an approach would be practical. Other approaches would be to change the size of the stope or the sequence of undercutting.
To summarize, the purpose of this presentation is to outline some aspects of the theory concerning the influence of block caving upon adjacent openings, show how this theory is supported by in-place measurements, and suggest logical approaches in designing mine workings and mine sequences to best suit the specific problems of the mining industry.