Because of the nature of the breakage in the Barmac vertical spindle impactor, the 80% reduction ratio is very small, so that when the energy efficiency is calculated by Bond’s method, it appears to be very low. However, the product size distribution contains a high proportion of fines. It is argued that the production of these fines accounts for the high energy consumption, and Bond’s method is modified to account for this, by considering the crusher to be, effectively, a number of smaller crushers in parallel, each having a different reduction ratio.
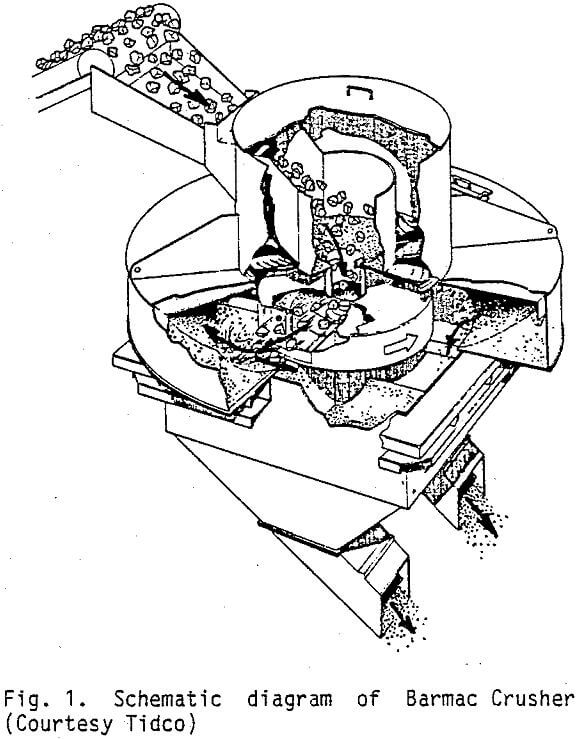
Because of the complex material flows in the crushing chamber, particle breakage is also complex. The wide range of particle sizes existing in the crushing chamber means that there are a wide range of energy intensities (energy/unit mass) for fracture. In turn this implies that the fracture mode will range from attrition, through cleavage, to shatter. Substantial breakage of daughter fragments must also occur.
Bond’s equation can be expressed as
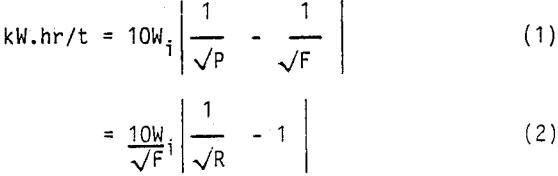
where P and F are the 80% passing sizes in the product and feed respectively, and R is the (80% passing) reduction ratio.
The procedure is to consider the product size distribution to be made up of a series of product size distributions that have the same shape as the total feed size distribution. This series of product size distributions can then be considered as arising from passage through a series of smaller crushers, operating in parallel, with differing reduction ratios.
From the top size fraction, it is possible to determine the split S1 which actually by-passes the crusher: it is given by
f1 x S1 = p1
where f1 and p1 are the mass fractions in the top size fractions of the feed and product size distributions, respectively.
Power consumptions were measured during the tests, and this data was used to generate regression correlations between feed rate and power draft. At 2220 rpm the relationship was
kW = 21.8 + 1.55(tonnes/hr)
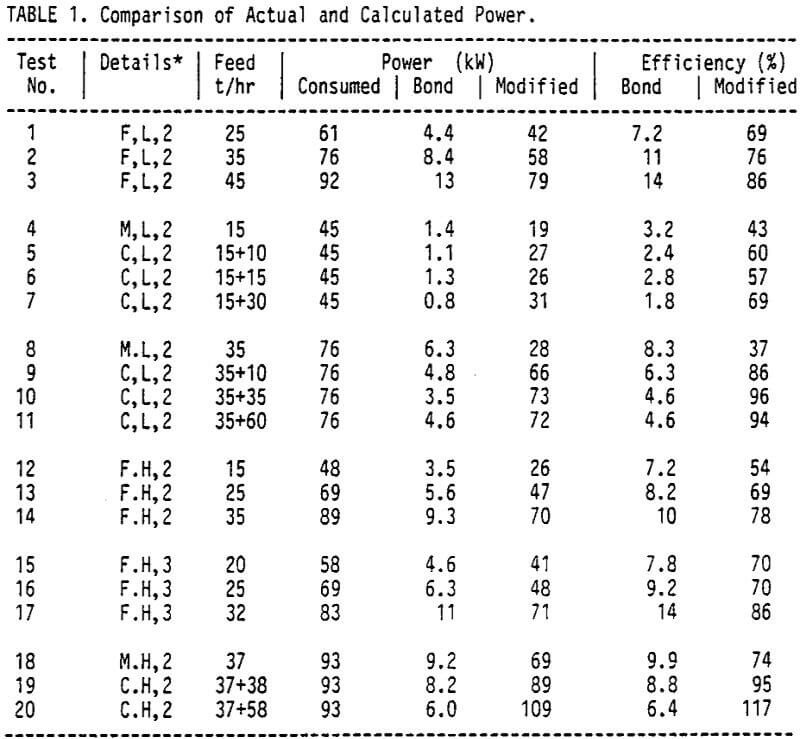
It can be seen that in terms of the conventional Bond calculation, the crusher appears very inefficient; typically less than 10%. In terms of the modified calculation, however, it can be quite efficient. In reality, the true efficiency will not be quite as high as this modified calculation implies. The reason for this is that all crushers, to some extent, have product size distributions that are wider than the feed distribution.
These modified efficiencies also indicate that, for a given feed rate, a higher rotor speed increases the efficiency, even although the power consumption is also increased.
In fact, in terms of the modified calculation, it is possible to achieve efficiencies of over 100%. It must however be noted that, in terms of the conventional Bond calculation, the efficiency generally decreases as the cascade feed increases.