Table of Contents
A numerical model is being developed to assess the enhancement of permeability by improved fracture connectivity by micro-hydrofracturing. A generic two-dimensional percolation model has been developed to test the impact of various field conditions on permeability. Field data from Cyprus Minerals’ Mineral Park Mine has been used to establish statistical properties of the observed fracture systems.
Collection of Fracture Data
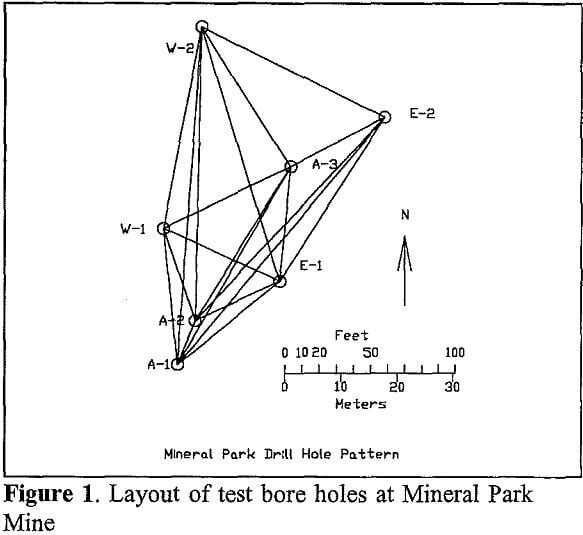
The primary source of fracture data was the borehole records obtained from seven rotary holes drilled at Mineral Park Mine. Bore hole geophysical logging was carried out by the USGS and included gamma, spontaneous potential, long and short normal resistivity, single point resistance, lateral resistivity, temperature, fluid resistivity, caliper, acoustic televiewer, and electrical induction. Identification of fractures intersecting the bore holes were made by using the acoustic televiewer images.
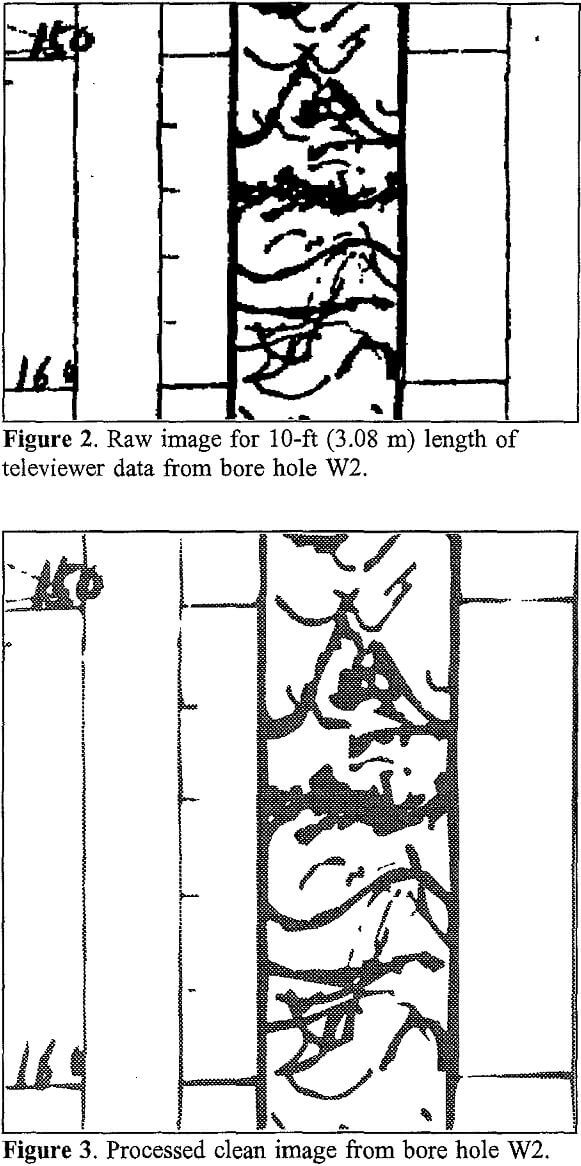
These image files were manually examined to identify and mark the fractures which intersect the logged section of the bore holes. After identifying all the fractures the following information has been obtained:
- Number of fractures as observed in each 10-ft section (3.048 m), of all bore holes. This provides a measure of fracture density as a function of depth and location.
- Fracture spacing as measured on a vertical line marked by the left edge of the televiewer images (the North wall of each bore hole).
- Probability of observing a fracture on a unit surface area. This is estimated by the ratio of the number of grid squares occupied by fractures to all grid squares within a 10-ft (3.048 m) section.
- Dip and azimuth of dip of each identifiable fracture.
Analysis of Fracture Data
Identifiable fractures were counted and recorded in each 10-ft (3.048 m) section of all seven bore holes. In total, 294 fractures were identified in 98 sections. Statistical analysis of the number of fractures per 10-ft (3.048 m) section indicates that this phenomenon can be represented by the Poisson distribution with mean m = 3.255.

This corresponds to 1.06 fractures per meter. This finding is also confirmed by the subsequent statistical analysis of fracture spacing.
Since there is a direct analytical link between Poisson and exponential distributions, it is natural that one would expect the fracture spacing be exponentially distributed such that if the corresponding Poisson distribution has m number of fractures per unit length, then the distance between any two fractures would be exponentially distributed with a mean equal to l/m units.
f(x) = m e -mx…………………………………………………………………………………(2)
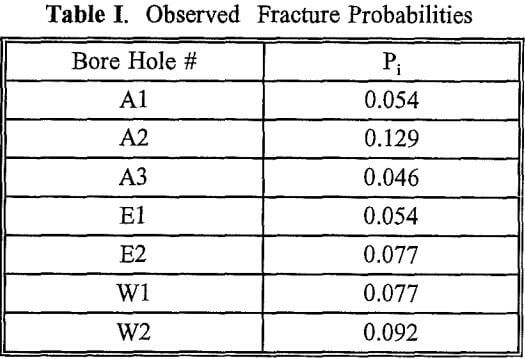
Probability of observing a fracture at any point in the rock mass (P) is a fundamental input needed in percolation modeling.
Percolation Modeling of Connectivity
A fundamental question in in situ leaching is that given a rock mass containing clusters of natural fractures, would there be a fracture cluster large enough to become a conduit between two bore holes separated by a given distance. The answer to this question is not trivially obtained without actually conducting physical tests. If any given two bore holes are not connected by any fracture cluster, then the fundamental question would be what kind of artificially generated fractures would establish a connection between these two bore holes.
The fundamental idea in percolation modeling is to consider a lattice (square, triangular, hexagonal, etc.,) to represent the medium to be modeled in a discrete fashion. The elements in the system can be the bonds between these lattice members (bond percolation) or the lattice members (site percolation) themselves. Each member (site or bond) would be considered occupied according to some predetermined probability p or not occupied (probability 1-p) . Two sites or bonds are considered connected if they share a common bond which is occupied. In either case, if p is small we have only small clusters of occupied sites, and there is no cluster which traverses the entire system. In order to accomplish this one needs to have at least one cluster of infinite length.
The percolation model presented above has only one parameter, p. In this case all sites are independently occupied . This generates a purely random structure with no directional anisotropics. In most cases, the fracture systems or joints in rock would present certain directional properties that have to be incorporated into the model. For example, data from Mineral Park Mine indicated that there are two main orientations around which the fractures seem to be aligned. In order to introduce directional properties into the system, the site occupation probability is modified conditionally.

