
For many years gravitational classification has been employed as a basic tool in beneficiation of minerals and coal. While improvements have been made to increase efficiency and fields of application, the basic flow pattern has remained relatively unchanged in most gravitational classifiers. Feed slurry is introduced into a settling pool wherein the coarser solids settle against either an upward or horizontal fluid current, or a combination of both, and are withdrawn in a concentrated underflow stream. The finer solids below the classification point possess too low a settling velocity and thus are primarily swept out through a weir overflow by the bulk of the fluid. Because of its simplicity, efficiency, and low power and maintenance costs, gravitational classification finds a wide acceptance for separations in the range of 20 to 325 mesh.
To test the applicability of the free vortex to gravitational classification, a 30-in. diameter open-top cyclone was constructed at Northwestern University. The cylindrical section was 30 in. high and the conical section included an angle of 60°. The feed nozzle was a standard 4-in. pipe entering tangentially, with centerline 17½ in. below the top of the cyclone. The conical section was flanged near
the apex to permit insertion of different 60° underflow cones with outlet diameters ranging from 5/8 to 1¾ in.
All runs were made on slurries containing ground agricultural dolomite of 2.83 sp gr. All particles were uniform in shape and specific gravity, and less than 1 pct were coarser than 20 mesh. The solids were charged to a 250-gal open tank equipped with a high speed mixer and water added to obtain correct solid concentration. A slurry pump fed the pulp to the open-top cyclone through a hand-operated throttling gate valve for control of flow rate. The overflow, underflow, and weir discharge returned to the slurry tank through launders or sheet metal conduits. Before any analyses or rate samples were taken, the system was allowed to pump for several minutes to attain equilibrium.
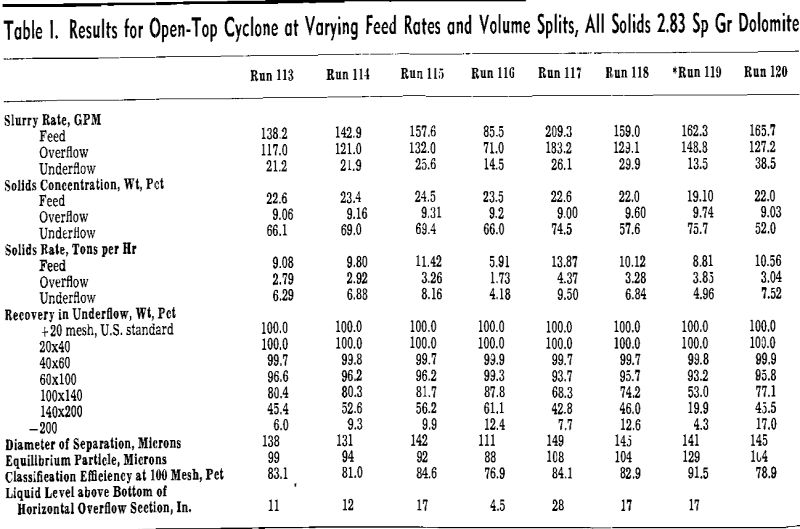
Effect of Overflow Rate and Volume Split: After many exploratory and test runs, it was established that the sharpest and finest classifications were obtained with a streamlined horizontal overflow section, and only one overflow discharge originating at the cyclone centerline. Several runs, therefore, were made at varying feed rates and volume splits to the underflow with constant feed solid concentration.
Two particle dimensions were calculated from the data: 1—diameter of separation, the diameter in microns at which 1½ pct by weight of the overflow solids would be coarser; and 2—equilibrium particle, the diameter of the particle in microns which is in equilibrium with the fluid currents at the critical separation point within the open-top cyclone. Theoretically, it is the particle size whose settling velocity is exactly equal to and opposite that of the radial velocity of the fluid at the radius separating the inner and outer spirals of the free vortex within the cyclone under the conditions of operation.
Therefore, the recovery per cent in the underflow for the equilibrium particle will be:
X = 100 – Y/2 + Y = 50 + Y/2…………………………………………….[1]
Where X = weight per cent recovery of the equilibrium particle size in the underflow
Y = per cent of feedwater reporting to the underflow.
Accordingly, from the underflow recovery curve for each run, the equilibrium particle size would be determined at the above per cent.
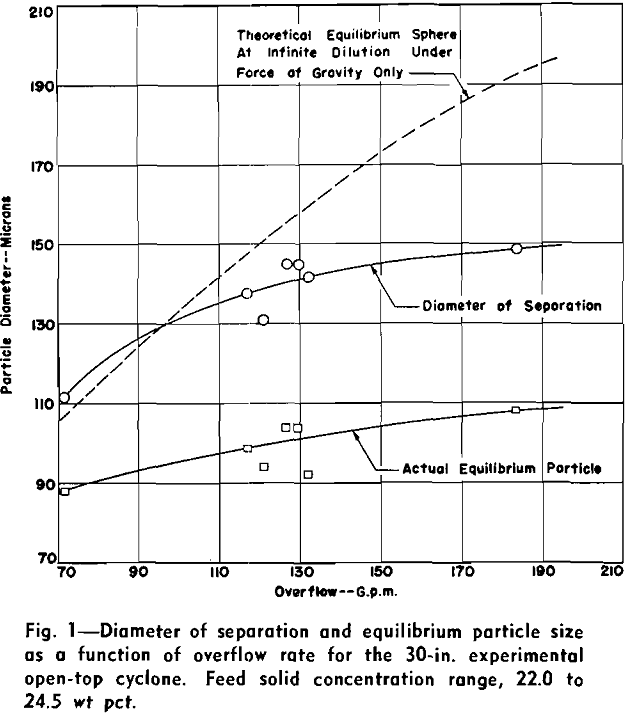
It should be pointed out that the equilibrium particle for conventional gravitational classifiers is generally felt to be best expressed by diameter of separation. All particles coarser than this size will be given a greater settling velocity, by the constant force of gravity, than that of the opposing fluid currents. However, this is not true for a free vortex, as neither the centrifugal force nor radial velocity is constant across any normal plane to the centerline. Accordingly, equilibrium separation occurs at the division between the inner spiral, directed toward the overflow, and the outer spiral, directed toward the underflow.
Sharpness of classification is indicated by efficiency of separation calculated from a formula by Taggart. Efficiencies ranged from 76.9 to 84.6 pct, which is generally considered high compared with efficiencies for gravitational classifiers.
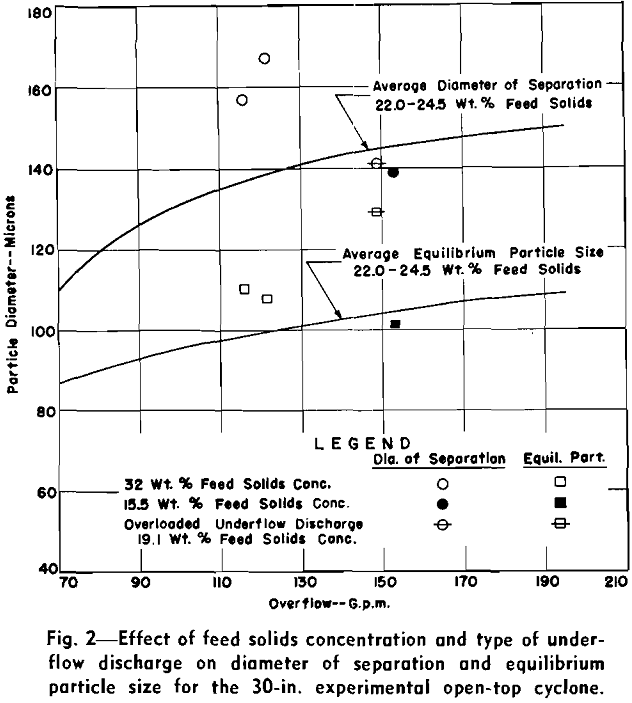
Effect of Feed Solids Concentration and Type of Underflow Discharge: Three runs, reported in Table III, were made at feed solids concentrations ranging from 15.5 to 32.1 pct.
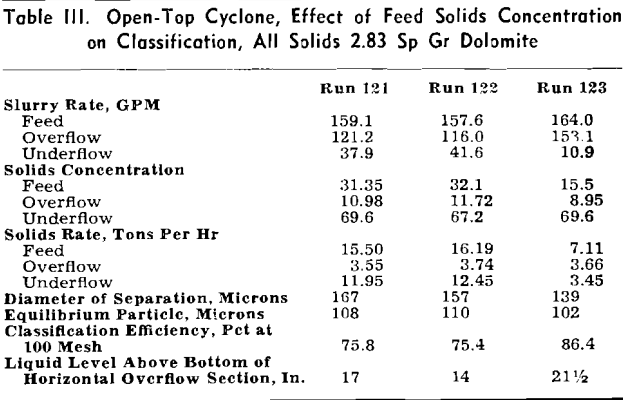
The results of Run 123 at only 15.5 pct feed solids concentration are slightly lower than the average conditions of 22.0 to 24.5 pct feed solids concentration. However, as only one run was made, this could be a statistical deviation. From previous conventional cyclone work, increase in equilibrium particle size on this material would be expected to begin at about 20 pet feed solids concentration.
During the exploratory runs overloaded underflow discharges were obtained in a few cases, but it was observed that overflow solids did not appear to increase in top size. This is contrary to experience with conventional cyclones with overloaded discharges wherein solid recovery in the underflow is very severely decreased and most of the particles are lost to the overflow.
The flow pattern was obviously more turbulent with the non-streamlined overflow, indicating that more of the initial fluid energy was not available for the centrifugal force. Accordingly the above results are to be expected. Consequently every effort should be made to present as little obstruction to the free vortex flow pattern with the open-top cyclone. This necessitates not only streamlined overflows but also smooth wall construction and continuous taper of the conical section.
The peripheral weir receives fluid from the outer radius of the free vortex. This radius possesses the lowest centrifugal force of the outer spiral wherein all separation must be achieved. Consequently, the higher diameter of separation is not surprising. However, the free vortex pattern is also distorted by such a weir discharge.
A line of slope 0.5, which would be anticipated by fluid mechanics theory, fit the data with sufficient accuracy. The equation for this straight line is:
gpm = 115√F………………………………………………[2]
where gpm = overflow rate, gal per min
F = height of slurry above bottom of horizontal overflow section, in feet of overflow slurry.
In a previous paper, the expression gpm/√F has been termed the capacity ratio. For a conventional cyclone, it was found equal to the following:
gpm/√F = K (eb)0.9……………………………………….[3]
where e = overflow diam, in.
b = inlet diam, in.
K = capacity ratio proportionality constant.

Using this equation with appropriate diameters of feed and overflow for the open-top cyclone, the capacity ratio proportionality constant would be 9.38. Conventional cyclones will normally exhibit values of this constant from 5.5 to 6.5.
It is not intended to imply that the open-top cyclone is entirely superior to other gravitational classifiers. Naturally each application will designate the type of classifier to be used. Rather, the comparisons will be made with respect to what is believed to be the specific advantage of the open-top cyclone: higher capacity per square foot at a relatively stable mesh of separation, with possibly sharper classifications.
