Table of Contents
A research program was conducted to improve processing technology for extracting alumina from nonbauxitic. The success of this program had provided the technology necessary for producing an adequate supply of high-grade alumina from domestic sources, thus meeting national economic and strategic needs relative to aluminum production. The hydrochloric acid process for recovering alumina from low-grade ores is one of the processes being investigated in the research program.
One phase of this process uses the effect of chloride-ion concentration on the solubility of aluminum ion in solution. At 25° C, the solubility of AlCl3 in pure water is approximately 31 pct by weight, and decreases with increasing concentration of hydrochloric acid (HCl), becoming 0.1 pct when the HCl concentration is increased to 37 pct. This behavior has been the subject of numerous investigations, processes, and patents. Thus it is possible to leach a nonbauxitic ore with HCl, decant and filter the liquor, and add gaseous HCl to precipitate out AlCl3·6H2O. The remaining acid solution can then be used for leaching additional ore and the precipitated AlCl3·6H2O can be calcined to obtain Al2O3 . An extensive discussion and evaluation of this process is presented by Peters, Johnson, and Kirby. Thermodynamic data, such as the ionic activities and the solubilities, required for complete analysis, interpretation, and improvement of this process are scarce, and the existing solubility data are limited to a narrow range of temperature. Therefore, the aims of this investigation were (1) to determine the solubility of AlCl3, in a temperature range of 25° to 85° C with HCl concentration from 0.0 to 37.2 pct; (2) to calculate the activities of AlCl3 and of H2O in solutions containing various electrolytes , and the equilibrium constant for the dissolution of AlCl3·6H2O; and (3) to suggest areas of research for generating useful data.
Apparatus
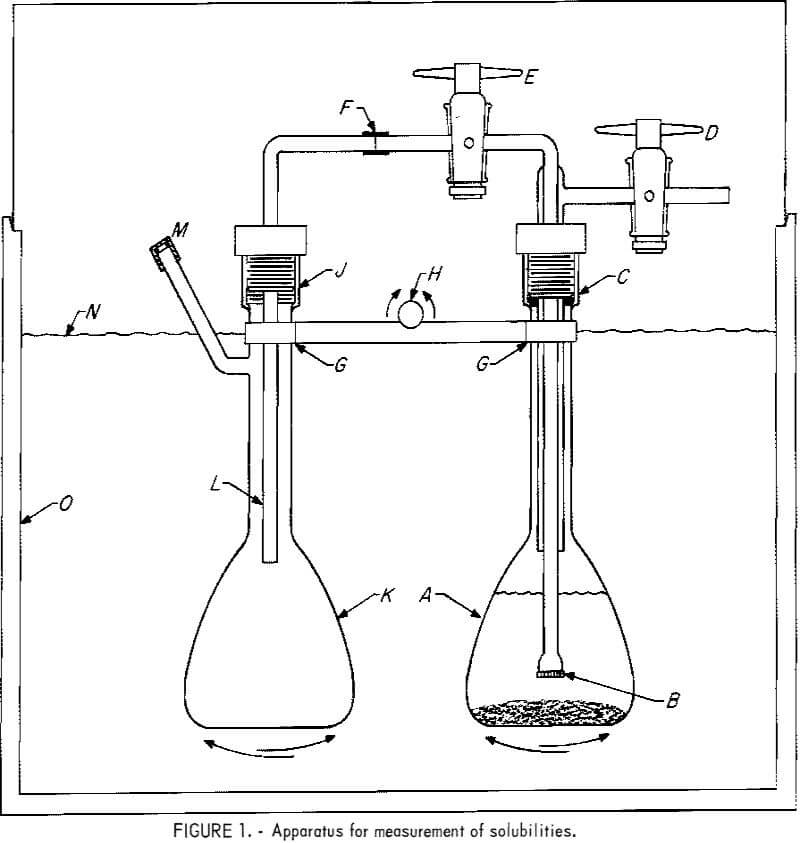
The apparatus used for measurements of solubilities is shown in figure 1. A 100-ml flask, A, contains a solution of electrolytes and some excess salt. A fritted glass filter, B, fused on a 6-mm-OD Pyrex tube is joined to an outer tube attached to two Teflon stopcocks, D and E. The top assembly is attached to A at C by a threaded nylon compression fitting with a neoprene 0-ring. A 6-mm-OD polyethylene tube, F-L, delivers a sample of solution filtered at B into the second flask, K, when A is pressurized through stopcock D, and E is opened. The fitting at J is similar to that at C. The flasks are clamped on a bar, G, which is attached to a rocking mechanism, with H as the axis of rocking for shaking the flasks, A and K, alternately up and down. A covered thermostat, 0, is controlled to within ±0.2° C. A closer temperature control is unnecessary since the solubility is a very weak function of temperature.
Experimental Procedure
Measurements of solubilities at 25°, 45°, 65°, and 85° C were made under conditions of phase equilibrium with analytical reagent-grade materials. Appropriate amounts of AlCl3·6H2O, 37-pct HCl solution, and distilled water were placed in flask A to form approximately 90 ml of solution with a small amount of excess salt crystals (hereafter “salt” refers to aluminum chloride hexahydrate). The amounts of materials were estimated from the existing solubility data on the ternary system AlCl3·6H2O-HCl-H2O. After the solution was formed in flask A and the apparatus was assembled, it was immersed in the water to level N, and the thermostat was set to the desired temperature. A continuous mechanical agitation of the flasks was used during each run lasting 2 to 3 days. Periodically, vigorous manual agitation was also used to assure
equilibrium, particularly if the salt could form a complex solid salt with HCl. At the end of the equilibration period, the flasks were allowed to remain motionless in an upright position for 1 hour to insure settling of solid particles. Stopcocks D and E were then opened to transfer approximately half of the solution into the sampling flask, K. The level of B below the liquid in A usually determined the amount of solution transferred into K. The weight of the solution in K was determined by weighing the flask before assembling and after admitting the solution and disassembling. A known amount of distilled water was injected into the flask through L to dilute the sample and dissolve any vapor in the gas phase. The partial pressure of HCl in pure water exceeds 1 torr at 25° C at molalities in excess of 8 m (m after a number in a sentence denotes molal); therefore, at concentrations less than 8 m it is doubtful that any loss of HCl could occur during sampling. For this reason, some of the runs at 25° C, containing less than 4 m HCl, were made with a single stoppered flask, and, after equilibration, a portion of the solution was carefully decanted and filtered for sampling.
Analysis
The solutions were analyzed after appropriate dilutions for total chloride-ion and aluminum-ion concentrations. The total chloride-ion concentration was determined by potentiometric titration with Ag+. The Al+++ concentration was determined by first complexing with an excess of ethylenediamine-tetraacetic acid (EDTA) and then back titration of the excess EDTA with Cu++ at a pH of 3.8.
The AlCl3 content was calculated from the Al+++ analysis. Subtraction of the chloride-ion in the calculated amount of AlCl3 from the total chloride- ion concentration allowed calculation of the HCl concentration in the saturated solutions.
This method of calculation was used for all analyses except those in which the HCl concentration was known to be zero, that is, when AlCl3 was the only electrolyte in pure water. For these analyses, the AlCl3 concentration was simply calculated from the chloride-ion analysis, which was the more accurate of the two analyses, although both Al+++ and Cl- analyses were still completed for these samples.
The difference in Cl- analysis computed from the total Cl- analysis and Cl- from Al+++ analysis for experiments without added HCl was ±0.2 wt-pct Cl-. This indicates that, on the average, the analysis of Al++ was subject to +0.05 wt-pct error, since the Cl analysis was known to be considerably more accurate than the Al+++ analysis. In solutions containing HCl, an error of ±0.05 percent in Al+++ content was reflected as ±0.20 pct in HCl content; this was because, while the total Cl content was very accurate, the Cl contributed by added HCl and, hence the molality of HCl, was computed by difference as mentioned earlier.
Results
The results are summarized in table 1 and shown in figure 2. The maximum HCl concentration for the data given in table 1 for 85° C is approximately 30 wt-pct. Measurements were stopped at this concentration because of the excessive equilibrium pressures in the system at higher concentrations. It should also be noted that fewer determinations were carried out at 65° and 85° C than at 25° and 45° C. Replicates were run at the two lower temperatures to give an indication of satisfactory repeatability of results. Figure 2 shows that the solubility of aluminum salt decreases drastically with increasing HCl concentration. Therefore, leaching nonbauxitic ores with HCl solution and precipitating out the pure salt for extraction of aluminum by adding HCl is a feasible process; such a process has been the subject of several patents. The results show that the solubility does not greatly change with temperature, and for a temperature increase of 60° C (25° to 85° C), the solubility of pure salt alone in water increases only 2.2 pct relative to solubility at 25° C.

Comp arison With Other Data
arison With Other Data
The solubility of pure salt in water at 25° C was found to agree exactly with the data of Palitzch and with Ehret and Frere. Results given by Malquori are about 10 pct higher. The solubility obtained by Tanaka is about 3.3 pct higher than in the present investigation at 45° and at 65° C.
The effect of HCl in water on the solubility of salt has been investigated by Seidel and Fisher at 0° C and by Malquori at 25° C. The results of the former investigators at 0° C agree very closely with the data in table 1, extrapolated to 0° C, whereas those of the latter investigator at 25° C scatter somewhat and disagree roughly by 3 pet at low HCl concentrations; however, the agreement in the range of 5 to 30 wt-pct HCl is within 1 pct.
Thermodynamic Treatment
Solubility Product and Activities in AlCl3·6H2O-H2O System
The ionic activity coefficient Y12 of AlCl3 in water has been measured up to 1.8 m by Mason, and recalculated values are given by Robinson and Stokes. Since the activity coefficient from 1.8 m to the saturation value of 3.3835 m is expected to increase more than fivefold, the saturation value is used for calculation by the method described in detail in a previous report (1 m = 1 mole in 1 kg of solvent). The method, with its appropriate novel application, is briefly summarized in this report. The mean ionic activity of AlCl3, designated as a12, is expressed by the following power series in terms of molality m:

The corresponding equation for the activity of water aw, is obtained by the application of the Gibbs-Duhem relation; the result is
![]()
Note that the exponents of m with the same coefficients of C, D, etc., are 1 higher in equation 2 than in equation 1, and the coefficient of m in equation 2 originates from the Debye-Huckel theory as discussed by Gokcen.
The reaction for dissolution of the salt is
AlCl3·6H2O (S) = Al+++ + 3Cl- + 6H2O (l),………………………….(3)
where (s) means solid and (l) liquid.
The corresponding equilibrium constant is
![]()
where the denominator, the activity of solid, is taken as unity since its composition remains unchanged when other electrolytes are added in solution. We substitute for a12 in 1n Kp directly from equation 1 and for aw from equation 2 after multiplying equation 2 by 0.108093 to make the coefficient of 1n aw equal to 6. Since Kp is composition independent, it is evident that
![]()
After the required substitutions from equations 1 and 2 and then the substitution of the average value m = 3.3835 from the first two runs in table 1, one equation is obtained for solving the six unknown coefficients in equation 1, and the remaining five equations are obtained by substituting each of the five experimental values of the mean ionic activity coefficient of AlCl3 , y12 in table 2, into
![]()
and then substituting each result in equation 1. Six simultaneous equations obtained in this manner are then solved by computer. The results are as follows:
C = -57.5723,
D = +142.0288,
E = -202.5581,
F = +161.1919,
G = -67.7831,
and H = +11,6880.
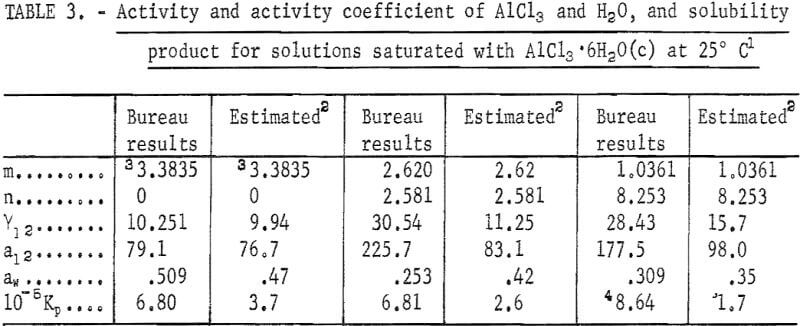
Substitution of these values in equations 1, 2, and 4 yields the values of Y12, aw, and Kp. The results are listed in table 3 under the heading “Bureau results:” It should be noted that the activity of water can now be calculated from equation 2, and the vapor pressure of water over the solution, P, from
aw = P/P°,……………………………….(7)
where P° is the vapor pressure of pure water at the same temperature. Note that the vapor pressure of water over the saturated solution is a little more than half of that over pure water since aw = 0.509. The foregoing results constitute the first set of data on activities based on the solubility of the salt.

Note.-In this table, m refers to the molality of AlCl3, n refers to the molality of HCl, and molality is moles in 1 kg of water.
Note.-In this table, m refers to the molality of AlCl3, n refers to the molality of HCl, and molality is moles in 1 kg of water.
Estimation of Activities in AlCl3·6H2O-H2O System
Two existing reliable methods of estimation are used to obtain the activities in AlCl3·6H2O-H2O system beyond the existing direct experimental data at m = 1.8. The first method, as described by Kusik and Meissner, gives an estimated value of γ12 = 9.94 at 3.3835 m. This estimated value is in close agreement with 10.251, the value obtained in the present investigation. The corresponding estimated value of the activity of water, aw, is 0.47, again in close agreement with the value of 0.509 found in the present investigation. The equilibrium constant Kp calculated from these values is not far from 6.8 x 10 5, considering the fact that the fourth power of a12 and the sixth power of aw are multiplied to obtain Kp.
The second method of estimation due to Bromley yields 10.42 for γ12, a value closer than that obtained by the preceding method. The activity coefficient of water has been obtained by the present authors, by integrating the Gibbs-Duhem equation in which the values of a12 estimated by the Bromley method were used. The result is aw = 0.540. The average of both methods is 0.505, which is in very good agreement with the Bureau’s value of 0.509. The Bromley method, however, does not contain a convenient method for determination of aw included in the Kusik-Meissner method.
The agreement of the estimated values with the values from the solubility data is not always as good as shown here for every electrolyte at every composition. For example, even for AlCl3 at 1 m, the two estimates of γ12 differ by only 13 percent from each other.
Solubility product and activities in AlCl3·6H2O-HCl-H2O system
The effect of increasing concentration of HCl on the solubility of the salt is largely due to the increasing concentration of the chloride ions. The equilibrium constant in this case with the activities a1 and a2 of individual ions is
![]()
where γ12 = γ1γ2 by definition of γ12 from the individual ionic activities γ1 (for Al+++) and γ2 (for Cl-), and n is the molality of HCl. The value of Kp is the same as that for equation 4 but the right side in equation 8 is dif¬ferent from that in equation 4. It may be noted that as n increases, m, the concentration of Al+++, must decrease, provided that γ12 and aw do not decrease greatly; therefore, the salt precipitates out, which is known as the salting out effect.
The calculation of the activities in the ternary solution requires an equation similar to equation 1 for HCl. Since the data for HCl are known accurately over a wide range of concentration, it is possible to take an equation with as many variables as desired. The following equation gives an accurate representation of the data for the activity coefficient of HCl, γ32 where the subscript 3 is for H+ and 2 for Cl-:
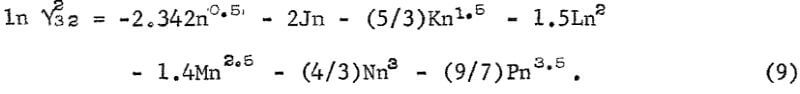
The data selected for this purpose from Haase, Naas, and Thutnm are listed on the third and fourth rows of table 2. The values of the coefficients calculated from these data are as follows:
J = -1.88416,
K = +2.24342,
L = -1.98545,
M = +1.00091,
N = -0.25934,
and P = +0.02634.
The equations for the activities of AlCl3 and of H2O contain these coefficients as well as the coefficients of the cross products (m h/2)(n k/2), where h and k are integers, and these equations are as follows:

The five additional coefficients in these equations are determined by adding equation 10 and 6 1n aw from equation 11 to obtain 1n Kp and by using the following selected solubility data from table 1:
m: 2.620, 2.016, 1.333, 0.953, and 0.535.
n: 2.581, 4.460, 6.780, 8.397, and 10,063.
The resulting calculations yield the following values of the coefficients in equations 10 and 11:
Q = +23,27027,
S = -22.47064,
U = +4.29102,
V = -9.76081,
and W = +4,60246.
The results for γ12, a12, aw, and Kp calculated from the preceding equations are listed in table 3. The values of γ12 from equation 9 are in agreement with those by Harned and Gary at very low concentrations of HCl and AlCl3.
The partial pressure of HCl(g), P32, over a solution can be calculated from the following equation (4):
Kp (HCl) = 4.94 x 10 -7 = P32/a²32………………………….(12)
where Kp(HCl) is the equilibrium constant at 25° C for H+ + Cl- = HCl(g), and a32 is the mean ionic activity of HCl in solution. For this purpose, it is necessary to write an equation for a32, similar to equation 10, by using the parameters in equation 11, as shown elsewhere in detail.
The effect of temperature on the solubility of the salt is small, as shown in table 1. The effect on the ionic activities is therefore expected to be small since all the parameters in equation 11 could have been obtained from the solubility data if the experimental error were smaller than ±0.01 wt-pct for aluminum analysis. In general, for a range of temperature up to approximately 80° C, each parameter is a linear function of temperature, and this dependence can be determined if equation 11 were known at another temperature at least 50° C higher than 25° C.
Estimation of Activities in AlCl3·6H2O-HCl-H2O System
The values of activities, activity coefficient, and the solubility product estimated in the present report according to the method devised by Kusik and Meissner, are listed in table 3. The activity coefficient γ12 for AlCl3 is roughly twice as high as the estimated value for the selected solutions containing HCl. The activity of water, aw, however, agrees well with the estimated values except for m = 2.620. It is evident that the calculations would have been considerably more reliable if the vapor pressure of water, aw, were measured because aw enters in Kp as aw, so that small errors in aw cause large errors in γ12 and Kp . For this purpose, a limited number of vapor pressure measurements are recommended to test the accuracy of the present calculations and the methods of estimation.
The temperature dependence of the thermodynamic properties listed in table 3 can be estimated as described by Kusik and Meissner. However, the estimate is likely to yield a higher degree of temperature dependence than that indicated by the weak temperature dependence of the solubility. No attempt could be made to calculate the effect of temperature by the Bureau’s method because (1) a12 at low concentrations of AlCl3 is not known at various temperatures, (2) the solubility of AlCl3 could not be determined with an accuracy approaching 0.01 pct in Al+++, and (3) the range of concentration of HCl at 65° and 85° C is too small for selecting a sufficient number of widely differing solubility data for AlCl3 to determine accurately the parameters in equations 10 and 11.
 AlCl3-FeCl3-KCl-NaCl-HCl-H2O System
AlCl3-FeCl3-KCl-NaCl-HCl-H2O System
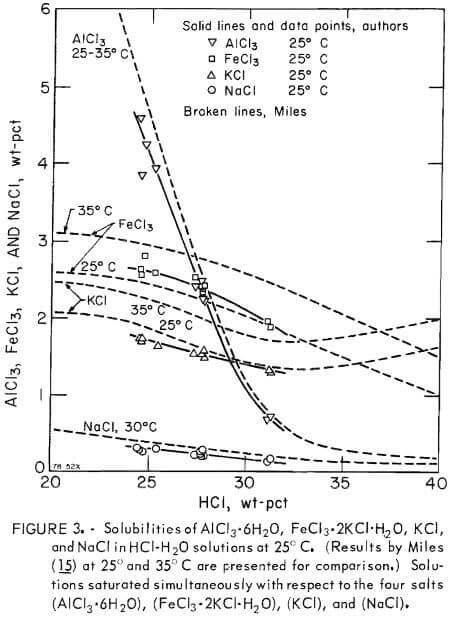
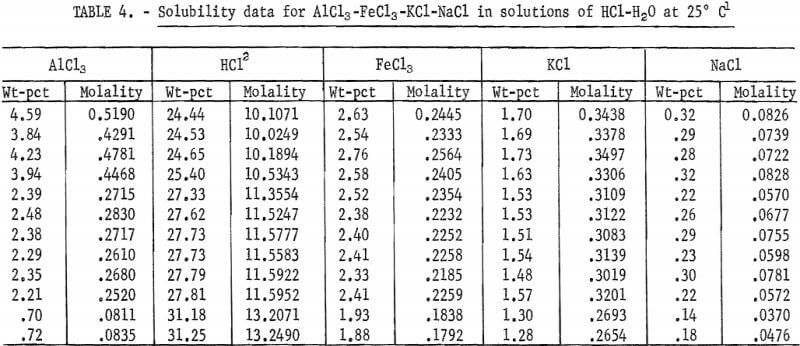
Preliminary data on solubilities of AlCl3, FeCl3 , KCl, and NaCl in aqueous solutions containing 24 to 31 wt-pct HCl at 25° C were obtained to assess contamination of AlCl3·6H2O extractable from nonbauxitic ores. For this purpose, 2 liters of a solution containing known amounts of salts were prepared, 90 ml of this solution were placed in a flask for each run and then a known amount of gaseous HCl was admitted to attain 24 to 31 wt-pct of dissolved HCl. In this range of HCl in solution, colorless anisotropic crystals of AlCl3·6H2O, bright anisotropic crystals of FeCl3·2KCl·H2O, and cubic isotropic transparent crystals of KCl and NaCl were precipitated and identified by microscopic examination. The procedure and analyses for aluminum-ion and chloride-ion concentrations were the same as those used for the AlCl3·6H2O-HCl-H2O system presented earlier in this report. In addition, the ferric-ion concentration was determined by standard K2Cr2O7 titration, the sodium-ion concentration was determined by atomic absorption techniques, and the potassium-ion concentration was determined by subtraction of the sodium-ion concentration from a determination of the combined potassium-ion plus sodium-ion concentrations after separation by ion-exchange. The results are listed in table 4 and plotted in figure 3. Similar results by Miles are also plotted in figure 3 to show that the agreement is excellent. Published data for related simpler systems containing fewer components have been compiled by Linke.
In the evaporative or HCl gas sparging crystallization processes for producing pure aluminum chloride hexahydrate, contamination by other metallic chlorides becomes a problem as impurity levels build up in leaching solutions. Figure 3 shows the concentration levels that impurities such as NaCl, KCl, and FeCl2·2KCl·H2O will also crystallize from solution as distinct separate phases, thus causing contamination of the AlCl3·6H2O crystals. For example, at less than 2.4 wt-pct FeCl3 in the presence of 1.6 wt-pct KCl at 25° C, the concentration of HCl must be less than 28 wt-pct to avoid contamination of AlCl3·6H2O by the double salt, FeCl3·2KCl·H2O. Figure 3 is also useful in redissolving the precipitate fractional recrystallization to purify the aluminum salt. In addition, some of the transition element salts, such as FeCl3, can be minimized by partial electrolysis to plate out a sufficient amount of iron prior to acidification with HCl.
A thermodynamic treatment of the system with the usual error of ±0.05 wt-pct in chloride-ion concentration is not feasible, particularly in the absence of vapor pressure data for H2O(g) and HCl(g). However, rough estimates of the activities can be made by the Kusik-Meissner method. It is anticipated that such estimates could give only rough values of the activities for the hydrated and complex salts and for the water.
Areas Recommended for Research
The measurements of activities are useful in interpreting thermodynamics and kinetics of leaching, precipitating, and purifying desired components of various ores. There are two reasons that the activities can be determined accurately from the measurements of vapor pressure of water: (1) The vapor pressure can be measured with a high degree of precision by differential pressure transducers to obtain aw by equation 7 and then to calculate the values of the parameters in equation 11 so that all the related properties can be computed as discussed previously in detail (2) The solubility product and the activities can both be determined accurately for multivalent salts that contain large numbers of water molecules in their hydrated crystals. The second reason arises from the fact that the exponent of the activity of water in equation 4 is equal to the moles of water in the hydrated crystal.
Aluminum Chloride in Aqueous Hydrochloric Acid Solutions
Another interesting type of experiment for the ternary system discussed here is the measurement of the partial pressure of HCl(g) over various solutions containing sufficiently large amounts of dissolved HCl. The experimental procedure for this purpose is described elsewhere. Group IIA, IIIA, and transition metal salts are excellent candidates for these types of investigations since electrolytes with higher valences than 1:1 usually form hydrated salts.
The solubility and the activity of aluminum chloride hexahydrate, AlCl3·6H2O, in aqueous solutions were determined as a part of the Bureau of Mines, U.S. Department of the Interior, research to improve mineral processing technology for recovering alumina from low-grade domestic resources. The solubility of AlCl3 in pure water was found to be 31.09 and 31.77 wt-pct at 25° and 85° C, respectively, and decreased drastically to 10 and 0.1 wt-pct when the respective amounts of 20.3 and 37 wt-pct hydrochloric acid (HCl) were added in solution. The equilibrium constant for the solubility of hexahydrate, activities, and activity coefficients of AlCl3 and H2O were calculated and compared with the results from the available methods of estimation. The results were shown to be useful in leaching nonbauxitic ores for extraction of alumina by changing the solubilities of component salts upon addition of HCl.
Simultaneous solubilities of AlCl3 , FeCl3, KCl, and NaCl in solutions of HCl-H2O were also determined and their effects on the purity of AlCl3·6H2O crystallized from mixed salt solutions are briefly discussed.
