Table of Contents
Surface-Energy of Liquids and Surface-Tension
The attractive forces mutually exerted between the interior molecules of a liquid produce at its surface the energy effects known as its “ surface-tension Within the mass of the liquid, each molecule attracts and is attracted by its neighbours with a force as intense as it is limited in range ; these internal attractions, which constitute cohesion, are mutually balanced, since, although the molecules in a liquid may be in rapid motion relatively to each other, their average spacing may be regarded as uniform. At the surface, however, the attractions cannot be evenly balanced, because no similar molecules exist beyond the boundary plane to counterbalance from that direction the requisite proportion of the attractive forces of the molecules which form the outermost layer. This unbalanced excess, distributed between the surface molecules and those immediately beneath them, produces a condition of strain or tension which tends to contract the area of the liquid surface to a minimum in much the same way as would a stretched rubber film ; it also imparts to the surface molecules a somewhat greater attractional pull towards the interior of the liquid than exists between molecules beneath the surface. The tension of a rubber film, however, increases with stretching, whereas that of a pure liquid remains constant; enlargement of the liquid surface simply results in more molecules being brought from the interior to the outer layer to satisfy the increase in area without any alteration of its surface-tension.
The effect of surface-tension in contracting the surface to minimum area accounts for the fact that drops of water falling through air and air-bells in water are spherical in shape, since a sphere has the smallest surface area for a given volume ; it also explains tire tendency of air-bells in a liquid to coalesce when brought into contact with each other, since the surface area of one sphere is less than the combined area of two spheres, each of half its volume.
Water has a greater surface-tension than almost all other liquids except molten metals. Due partially to this fact, a thin stream of falling water or a thin film of a liquid in air is at once broken into droplets. Stability can be imparted, however, by dissolving in the liquid a small quantity of certain foreign substances, such, for example, as soap, saponine, or amyl alcohol. Since the attraction exerted between the water molecules themselves is greater than that exerted between the water and foreign molecules of the above nature, the latter tend to be “shouldered out” to the boundary of the water and thus to be concentrated in its surface film (adsorption). Such an assemblage of molecules in the outermost layer not only reduces the surface-tension of the water but also supplies the mechanism whereby its thin films are stabilized, as in the case of soap bubbles in air, because, wherever in the films an area of greater tension may momentarily exist, thither will the foreign molecules be automatically pushed in greater number, thus relieving the local strain and re-establishing equilibrium.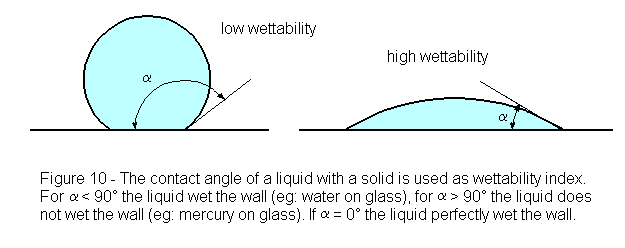
It is impossible to disseminate small air-bells effectively through a pure liquid owing to their instant re-coalescence, nor can a permanent froth be formed when they rise to the surface, as the films bounding the bubbles instantly break ; in fact, no froth can be formed with a pure liquid, but contamination with foreign molecules by reducing the surface-tension stabilizes both the air-bells in the liquid, preventing re-coalescence, and the bubble-films which result therefrom at the surface. The frothing reagents used in flotation are nothing more than suitable contaminants added to supply foreign molecules of the type most effective for the purpose.
Another effect of surface-tension is to confer upon the liquid surface a certain resistance to rupture, enabling it to support particles of greater density than its own, such as dust, particles of dry ore, water insects (“skaters”), and other bodies that are not immediately wetted, such as a slightly greased needle. This is referred to later.
Surface-Energy of Solids and Interfacial Tension
Although the molecules of a solid are relatively immobile compared with those of a liquid, a solid surface must also be considered as possessing energy due to unbalanced molecular forces similar to those exhibited by a liquid. In either case some of these attractive forces will operate in directions outside the boundary surface when the latter is brought into contact with other substances. Such forces may be conventionally considered as divisible into two components : (1) An attractive force capable of acting vertically to the surface, and (2) a tension exerted parallel with it. Thus, if a drop of water be placed in contact with a solid the surface-energy of both substances is partly expended across the interface between them as a mutual attractional reaction (adhesion), the remainder being exerted as a tension along it (interfacial tension) ; the resultant of these components with that of the liquid surface-tension determines the degree to which the solid is wetted.
Contact-Angle
All flotation processes are dependent upon the fact that different rock and mineral surfaces are “wetted” by water in varying degree. Although at first sight it may seem that any particle wholly submerged in water must be “completely” wetted, the extent to which it is actually capable of being wetted will be better appreciated on bringing it again into the air and observing the result. On withdrawal, some substances will be found to remain almost completely covered with a film of water, whilst the liquid may partially shrink from the surfaces of others and become heaped up into droplets. The angle made by the droplets with the dry face of the solid from which the water has receded is termed the “contact-angle” for the substance, and it varies with the nature of the solid. The degree of wetting possible for each substance is therefore indicated by the value of the contact-angle.
If the water completely films the solid surface and no withdrawal occurs, the contact-angle must evidently be zero ; this implies that the maximum degree of wetting has taken place and that a submerged particle of the substance will remain permanently sunken in the water, no matter to what air-bell contacts it may be exposed, but, should the water form a hemispherical droplet, the contact-angle here reaches a value of 90°. Such an angle indicates that a submerged particle, when brought into contact with an air-bell, will dispense with some of its water covering and adhere to the air so supplied ; if the particle is not too large, it will be lifted by the attached air-bell to the surface, forming with others a mineralized froth. The larger the contact-angle for any given substance, the greater is the extent to which water shrinks from its surface in favour of air, and consequently the greater its tendency to be floated ; the reverse is likewise true.
All practical flotation depends, therefore, on accentuating the factors of variable wetting into sufficiently “selective” wetting. This object is achieved by the use of various reagents, some of which produce “wetting” approaching the maximum for the unwanted gangue particles, by reducing the value of their contact-angles to the lowest possible figure, whilst others increase the contact-angles to moderately high values for the particles to be floated with consequent decreased “wetting”.
The relationship between the contact-angle, the solid and liquid surface-tensions, and the interfacial tension may be illustrated as follows :—Let A in Fig. 28 represent a droplet of water upon a solid surface B, heaped up to such an extent that its edges meet the solid surface, as at P, at an angle marked θ, which represents the contact- angle of water for this particular solid. As P is stationary for the time being, the forces acting upon it (also upon P¹ and all other points round the edge) are balanced and in equilibrium with each other. These contractile forces are three in number : (1) the surface-tension of the liquid, (2) S2, the surface-tension of the solid, and (3) S12, the interfacial tension of the solid/liquid contact. Since we are only considering the position of P upon the solid surface, it is evident that, whereas the forces S12 and S2 act with their full values parallel with the surface, only the resolved horizontal component of the tensional force S1 can act in such a direction, and therefore the force it exerts on P will be the fraction of its full amount represented by the cosine of the angle at which it acts—i.e., /S1cosθ. In this instance the resulting equilibrium which determines the contact-angle is expressed by the equation— S12 + S1cosθ = S2 since the component tensional forces which tend to pull P to the left are here balanced by the tension which tends to pull it to the right.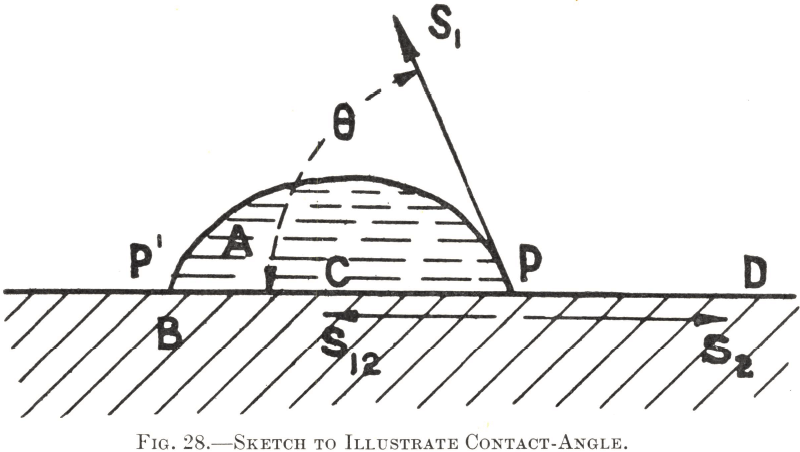
The interfacial component S12 represents the balance of the molecular attractions between the water and the solid which are not mutually engaged in producing adhesion across the interface. If the adhesive force between the two substances were to be increased by some means, the remainder S12 would be diminished, and P would no longer be held in equilibrium, but would be pulled towards D until a new equilibrium became possible. In other words, the water would spread further over the solid and its contact-angle would be correspondingly reduced. Were it pulled so far over the surface as to film it completely, the contact- angle would fall to zero and the maximum degree of wetting (adhesion) would be reached.
On the other hand if adhesion between the water and the solid were to be diminished the tensile force S12 would necessarily increase, and P, being no longer balanced by S2, would be pulled towards C. The water would then become heaped up still further, leaving a larger area of surface dry and making a greater contact-angle. Were no adhesion to occur at all between the liquid and the solid, the former would become a spherical drop, having no theoretical contact with the surface of the latter, and the contact-angle would reach 180°. The condition of absolute “non- wetting”, however, is unknown, the highest contact-angle measured so far being in the neighbourhood of 140° for a globule of mercury on glass.
Heavy particles which float at a liquid surface by virtue of its surface-tension do not, as might be supposed, lie merely cradled in a depression of the surface layer as in Fig. 29a, but partially penetrate it and remain suspended by the tensional force of the water film as in Fig. 29b. Here again the factor of the contact-angle (indicated in Fig. 29b by θ) comes into play. A particle having a low contact-angle will tend to sink, since the liquid invades so much of its surface and contracts the length of the water-edge suspending it to such an extent that insufficient tensional force remains to retain it. Conversely, a high contact-angle prevents the sinking of particles
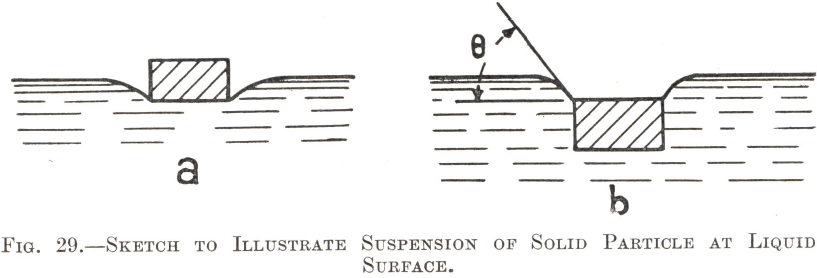
The “film flotation” process was based on the suspension of mineral particles in this way, finely ground ore being fed continuously upon the quiescent surface of a slow-moving stream of water, whereon the minerals of high contact-angle floated and were removed, whilst the gangue was wetted and sank. The method was inefficient in many respects and is now obsolete. One reason for its failure was that the area of water needed to handle a large tonnage of ore was so extensive as to render the process impracticable. The success of froth flotation, which is the only method in use at the present day, depends to a considerable extent on the fact that the air/water surface needed to handle large tonnages of ore is provided by means of a multiplicity of air-bells disseminated throughout a comparatively small volume of pulp.
Theoretical discussion of the tensional forces and their effects need not be carried further; enough has been said to indicate that the contact-angle is an index of the degree to which a liquid will wet a solid, its precise value being chiefly of academic interest. In practice it is sufficient to know the approximate relative “floatability” of one mineral in relation to another. There is, however, an interesting point about the contact-angle value for any solid/liquid contact—viz., that it is not completely unalterable but varies between two limiting values. This variation is termed the “hysteresis” of the contact-angle and is of great importance in imparting a certain flexibility to the water-edges at the points of contact. Thus the tangent to the air/water surface at the point P in Fig. 28, which makes the angle θ with the solid, can hinge to some extent round P in either direction without causing the water-edge to shift or break away from this point. It is due to this property that an air-bell in water, to which particles have become attached, will withstand a certain amount of rough handling and deformation without dropping its mineral load.
