The relation of the weight of a substance to its volume should be kept in mind in all cases where both weight and volume are dealt with. Students are apt to imagine that on mixing equal volumes of, say, sulphuric acid and water, an acid of half the strength must be obtained. If the statement of strength is in parts by weight this will lead to considerable error. For example, 100 c.c. of sulphuric acid containing 98 per cent, by weight of real acid, will, if diluted with 100 c.c. of water, yield a solution containing not 49 per cent, by weight, but about 63.5 per cent, of the acid. The reason is this : the 100 c.c. of sulphuric acid weighs 184 grams, and contains 180.32 grams of real acid, while the 100 c.c. of water weighs only 100 grams; the mixed water and acid weighs 284 grams, and contains 180.32 of real acid, which is equivalent to nearly 63.5 per cent, by weight. If, however, the method of statement be volumetric, it would be correct to say that doubling the volume halves the strength : if 100 c.c. of brine contains 10 grams of salt, and is diluted with water to 200 c.c., it would be of one-half the former strength, that is, 100 c.c. of the solution would contain 5 grams of salt.

This confusion is avoided by always stating the strengths as so many grams or “ c.c. ” in 100 c.c. of the liquid. But obviously it would be advantageous to be able to determine quickly the weight of any particular substance corresponding to 1 c.c. or some other given volume. Moreover, in descriptions of processes the strengths of acids and solutions are frequently defined neither by their gravimetric nor volumetric composition, but by a statement either of specific gravity or of the degrees registered by Twaddell’s or Beaume’s hydrometer. Thus, in the description of the process of gold parting, one writer gives : “ The acid should be of 1.2 specific gravity”; and another says: “The acid must not be stronger than 32° Beaume.”

These considerations justify an account of the subject in such a work as this. And on other grounds the determination of a specific gravity is one of the operations with which an assayer should be familiar.

The meaning of “ specific gravity ” is present in the mind of every one who uses the sentence “ lead is heavier than water.” This is meaningless except some such phrase as “ bulk for bulk ” be added. Make the sentence quantitative by saying : “ bulk for bulk lead is 11.36 times heavier than water,” and one has the exact meaning of: “ the specific gravity of lead is 11.36.” A table of the specific gravities of liquids and solids shows how many times heavier the substances are than water.

It is better, however, to look upon the specific gravity (written shortly, sp. g.) as the weight of a substance divided by its volume. In the metric system, 1 c.c. of water at 4° C. weighs with sufficient exactness 1 gram ; consequently, the sp. g., which states how many times heavier than water the substance is, also expresses the weight in grams of one c.c. of it. So that if a 100 c.c. flask of nitric acid weighs, after the weight of the flask has been deducted, 120 grams, 1 c.c. of the acid weighs 1.2 gram, and the sp. g. is 1.2. The specific gravity, then, may be determined by dividing the weight of a substance in grams by its volume in c.c.; but it is more convenient in practice to determine it by dividing the weight of the substance by the weight of an equal volume of water. And since the volumes of all substances, water included, vary with the temperature, the temperature at which the sp. g. is determined should be recorded. Even then there is room for ambiguity to the extent that such a statement as the following, “ the specific gravity of the substance at 5o° C. is 0.9010,” may mean when compared with water at 50° C. or 4° C., or even 15.5° C. For practical purposes it should mean the first of these, for in the actual experiments the water and the substance are compared at the same temperature, and it is well to give the statement of results without any superfluous calculation. In the metric system the standard temperature is 4° C., for it is at this point that 1 c.c. of water weighs exactly 1 gram. In England, the standard temperature is 6o° F. (15.5° C.), which is supposed to be an average temperature of the balance- room. The convenience of the English standard, however, is merely apparent; it demands warming sometimes and sometimes cooling. For most purposes it is more convenient to select a temperature sufficiently high to avoid the necessity of cooling at any time. Warming to the required temperature gives very little trouble.

Specific Gravity Determination 

There is a quick and easy method of determining the density or sp. g. of a liquid, based upon the fact that a floating body is buoyed up more by a heavy liquid than by a light one. The method is more remarkable for speed than accuracy, but still is sufficiently exact. The piece of apparatus used for the purpose is endowed with a variety of names—sp. g. spindle, hydrometer, areometer, salimeter, alcoholimeter, lactometer, and so on, according to the special liquid upon which it is intended to be used. It consists of a float with a sinker at one end and a graduated tube or rod at the other. It is made of metal or glass. Generally two are required, one for liquids ranging in sp. g. from 1.000 to 2.000, and another, which will indicate a sp. g. between 0.700 and 1.000. The range depends on the size of the instrument. For special work, in which variations within narrow limits are to be determined, more delicate instruments with a narrower range are made.

In using a hydrometer, the liquid to be tested is placed in a cylinder (fig. 34) tall enough to allow the instrument to float, and not too narrow. The temperature is taken, and the hydrometer is immersed in the fluid. The mark on the hydrometer stem, level with the surface of the liquid, is read off. With transparent liquids it is best to read the mark under and over the water surface and take the mean.

The graduation of hydrometers is not made to any uniform system. Those marked in degrees Baume or Twaddell, or according to specific gravity, are most commonly used. The degrees on Baume’s hydrometer agree among themselves in being at equal distances along the stem; but they are proportional neither to the specific gravity, nor to the percentage of salt in the solution. They may be converted into an ordinary statement of specific gravity by the following formulae :—

Sp. g. = 144.3/144.3 – degrees Baume.

or putting the rule in words, subtract the degrees Baume from 144.3, and divide 144.3 with the number thus obtained. For example : 32° Baume equals a sp. g. of 1.285.

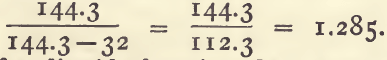
or putting the rule in words, subtract the degrees Baume’ from 144.3, and divide 144.3 with the number thus obtained. For example ; 32° Baume equals a sp. g. of 1.285.

144.3/144.3 – 32 = 144.3/112.3 = 1.285

This rule is for liquids heavier than water ; for the lighter liquids the rule is as follows :—

Sp. g. = 146/136 + degrees Baume

or in words divide 146 by the number of degrees Baume added to 136. For example : ammonia of 30° Beaume has a sp. g. of 0.880 (nearly).

146/136 + 30 = 146/166 = 0.8795.

A simple series of calculations enables one to convert a Beaume hydrometer into one showing the actual sp. g. Graduation, according to sp. g. is the most convenient for general purposes. In these instruments the distances between the divisions become less as the densities increase.

Twaddell’s hydrometer is graduated in this way : Each degree Twaddell is 0.005 excess of unity. To convert into sp. g. multiply the degrees Twaddell by 0.005, and add 1. For example: 25° Twaddell equals a sp. g. of 1.125.

25 x .005 = 0.125; + 1.000=1.125.

There is a practice which ignores the decimal point and speaks of a sp. g. of 1125 instead of 1.125. In some cases it is convenient, and inasmuch as no substance has a real sp. g. of much over 20, it can lead to no confusion. The figures expressed in this way represent the weight of a litre in grams.

Some hydrometers are graduated so as to show at a glance the percentage composition of the liquid they are intended to be used with. Gay-Lussac designed one to show the alcoholic strength of mixtures of alcohol and water; the construction of others upon the same principle is easy and perhaps useful. But when the principle is applied to complex liquids and mixed solutions, it is misleading.
The various methods of graduation ought all to give place to one showing a simple statement of the sp. g.

The method of determining sp. g. with the hydrometer is obviously inapplicable to the case of solids, and in the case of liquids it should not be used where exact figures are required. There are several other methods which may be used, but on the whole those with the specific gravity bottle are most convenient.

The specific gravity bottle (fig. 35) is a light flask of about 25 c.c. capacity, provided with a well-fitting perforated stopper. It is essentially a graduated flask, which measures a constant volume, but it does not much matter what the volume is.

In taking the sp. g. of a liquid (or, what is the same thing, a fused solid) there is wanted the weights (1) of the flaskful of water and (2) of the flaskful of the liquid. Dividing the second by the first gives the required sp. g. The actual weighings required are—

(1) of the dry and empty flask,
(2) of the flask filled with water, and
(3) of the flask filled with the liquid.

The weighing of the flask once made need not be often repeated. It is well to do so now and then for safety’s sake; but one weighing will serve for a large number of determinations. The same remarks apply to the weighing of the bottle filled with water. The bottle is dried by rinsing out first with alcohol and afterwards with ether; ether is very volatile, and a short exposure in a warm place will soon drive off the little remaining about the sides. The ether vapour should be sucked out through a glass tube. See that the bore of the stopper is dry as well as the bottle. Let the dry bottle stand in the box of the balance for a minute or two before weighing. The weight is, strictly speaking, not that of the empty bottle, but of the bottle filled with air. The empty bottle would weigh from 20 to 30 milligrams less. Correcting for this would, in most cases, only make a difference in the fourth place of decimals, so that it is better to ignore the error.

The weight of the flask filled with water is got by filling it with distilled water, and inserting the stopper. The excess of water will overflow at the margin and through the bore. The bottle is wiped with a soft, dry cloth, taking care not to squeeze or warm the bottle. The bottle will remain filled to the top of the stopper. It is allowed to stand in the balance box for a minute or two, and then weighed.

Distilled water, as stated, should be used; the use of ordinary water may increase the weight by 5 or 6 milligrams. Many waters, if they have not previously been boiled, give off bubbles of air which render the weighing worthless.

The temperature of the water is of greater importance; lowering the temperature 2° will increase the weight by 10 or 12 milligrams. A beaker of water may be warmed or cooled to the required temperature; then the bottle is filled from it, and quickly weighed. If the balance-room is cooler than the water, the latter will draw back into the bottle, and a few small bubbles of air will enter; but even in extreme cases this will only increase the weight by a very small fraction of a milligram. There is more trouble caused when the room is warmer, for the liquid then expands and protrudes as a drop resting on the top of the stopper.

There will in this case be loss by evaporation, which in the case of the more volatile liquids, such as alcohol, is serious. To prevent this loss, as well as any that may arise by overflow, the stopper should be dilated above into a small cup, A (fig. 36), which may itself be stoppered. In a bottle of this kind the neck of the stopper is graduated, and the bottle is considered full when the liquid stands at the level of the mark in the neck. On inserting the stopper, the liquid rises into the cup, and is reduced to the level of the mark by absorption with pieces of filter-paper.

For most purposes, however, there is no need for cooling and allowing room for subsequent expansion.
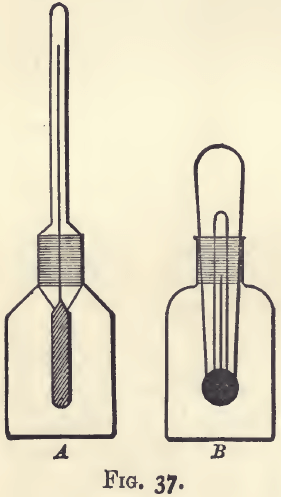
The assayer, as a rule, can select his own standard Fig. 36. temperature, and may choose one which will always necessitate warming. It will be handier in this case to have a bottle with a thermometer stopper. Of the two types shown in fig. 37, that with the external thermometer tube (A) is more generally useful.

The bottle is filled at a lower temperature, and is then gently warmed so as to slowly raise the temperature to the required degree. The superfluous liquid is then at once wiped off, and the bottle cooled and weighed.

The weight of the flask filled with the liquid whose sp. g. has to be determined is ascertained in a similar way. Of course the temperature must be the same. If the liquid does not mix with water, the bottle should be dried before filling, but otherwise the flask need only be rinsed out two or three times with the
liquid.

Having obtained the three weighings, deduct the weight of the bottle from each of the others to get the weights of the water and liquid respectively. Divide the latter by the former, the result shows the sp. g. As an example, take the following, in which a rather large sp. g. bottle was used :—

By subtracting 1 from 2 and 3 the result is as follows :—

Divide the weight of the paraffin by that of the water—

The sp. g. of the paraffin is 0.7948.
The sp. g. of a fusible solid may be obtained in the same way at a temperature some degrees above its fusing point.

The sp. g. of a solid in powder or gravel sufficiently fine to pass through the neck of the bottle is easily determined. If the bottle filled with water weighs 50 grams, and there is placed on the pan alongside of it 20 grams of a sand, the weight of the two together will of course be 70 grams. But if the sand is put in the bottle, it evidently displaces its own bulk of water; and if, on again weighing, the weight is found to be 62 instead of 70 grams, it is because the 20 grams of sand has displaced 8 grams of water. Bulk for bulk, the sand is 2½ times as heavy.

In practice, the weight of the bottle filled with water will probably be already known; if not, it must be determined. A certain quantity, say 20 grams, of the powdered substance is then transferred carefully to the bottle. The bottle need not be dry inside, but its neck and outside must be. In making this transference a careful worker will make no loss, and the mode of working saves a little time. But it is better to weigh the dry flask ; put into it 10 to 20 grams of the powder, and weigh again. The increase in weight gives accurately the weight of powder in the bottle. About two-thirds fill the bottle with distilled water, and mix with the powder by gentle shaking. Air bubbles will disentangle themselves, and rise to the surface of the water. Wash back anything adhering to the stopper with a jet of water, and fill the bottle almost to overflowing. Allow it to stand for a minute or so ; replace the stopper ; warm to the required temperature ; take off the superfluous moisture; wipe and weigh. As an example, take the following :—

Subtract (1) from (3) to get the weight of wolfram taken:—

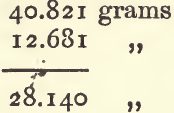
add the weight of the wolfram to the weight of the bottle filled with water :

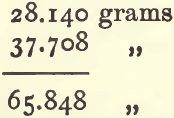
subtract (4) from this to get the weight of water displaced :

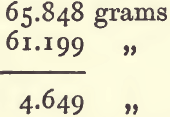
Divide the weight of the wolfram by the weight of the water displaced to get sp. g. :

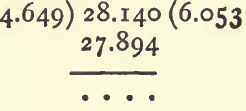
If the solid is soluble in water, or has a tendency to float, some liquid other than water is used. Paraffin oil or oil of turpentine will do. The process is as follows :—The weight of the dry and empty bottle having been determined, add a sufficiency of the substance and weigh again to find how much has been added. Fill up with paraffin oil and weigh again. Clean out the substance by rinsing with paraffin ; fill up and weigh. Calculate the sp. g. as if water had been used, and multiply by the sp. g. of the paraffin.

For example :

First from (1), (3), and (5), calculate the sp. g. of the paraffin as already shown. It will be 0.7948. Deduct (1) from (2) to get the weight of the nitre :

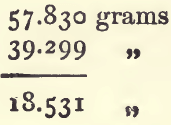
add this to (3) :

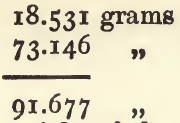
and deduct (4) to find the weight of the equal bulk of paraffin :

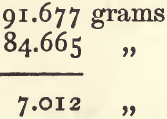
divide the weight of the nitre by the weight of the paraffin :

The sp. g., taking paraffin as the standard instead of water, is 2.6427. Multiply this by the sp. g. of paraffin, 0.7948, and the result is 2.1004 as the sp. g. of nitre compared with water.

Similarly, a sp. g. compared with water at say 50° C. can be converted into one compared with water at standard temperature, by multiplying by the sp. g. of water at 50° C. The following table gives the sp. g. of water at various temperatures :—

If, for example, a substance at 50° C. has a sp. g. of 0.9010 as compared with water at 50° C., it will have (compared with water at 4° C.) a sp. g. of 0.9010 x 0.9881; or 0.8903. The figures 0.8903 represent the sp. g. of the substance at 50° C. compared with water at 4° C. Except in comparing the sp. gravities of the same substance at different temperatures, a calculation of this kind serves no useful purpose.

In taking the specific gravity of a solid not in powder, a lump of it is freed from loose particles and its exact weight determined. By means of a horse hair with a slip knot it is suspended to the balance, and beneath it is placed, out of contact with the balance pan, a beaker of distilled water. The horse hair must be long enough to keep the mineral well beneath the surface of the water so as to allow the balance to vibrate. Air bubbles are removed by touching with a camel-hair pencil. Whilst the mineral is suspended in water the weight is again taken. It will weigh less than before, and the difference between the two weighings gives the weight of water (and consequently the volume) displaced by the mineral. The weight in air divided by the difference is the specific gravity. Thus

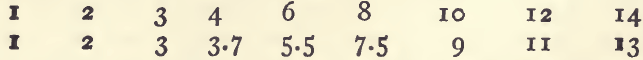
3. 2170 ÷ 0.5120 equals 6.28, the sp. g.

The sp. g. of a substance depends mainly on its composition, but is affected by certain conditions. The effect of temperature has been already considered. Air holes and empty spaces lessen the specific gravity of otherwise solid bodies; and metals, which after fusion become imperfect solids, have their density increased by hammering or rolling. But metals when free from pores have their density diminished when rolled, without annealing. The effects of these conditions are slight when compared with those due to the presence of impurities.

For simple substances, or mixtures of only two substances, a determination of sp. g. is a sufficient check on the composition for many practical purposes; and with more complex mixtures, such as slags and some of the products of dressing operations in which the material does not differ much in its nature from time to time, such a determination will yield information of considerable value, and afford a check upon the proper working of a process.

When the mixing of two substances is accompanied by a change in volume, the sp. g. of the mixture can only be learnt by experiment. But when the substances have no such action on each other the resulting sp. g. can be calculated. Some of these calculations have a practical interest as well as an educational value. Students should practise them so as to become familiar with the relations between weight and volume.

When substances are mixed by volume, the sp. g. of the mixture is the mean of those of its constituents, and may be calculated in the usual way for obtaining averages. 1 c.c. of a substance having a sp. g. of 1.4 mixed with 1 c.c. of another having a sp. g. of 1.0 will yield 2 c.c. of a substance having a sp. g. of 1.2. If, however, we write gram instead of c.c. in the above statement, the resulting sp. g. will be 1.16. The simplest plan is to remember that the sp. g. is the weight divided by the volume (sp. g. = w/v) and the sp. g. of a mixture is the sum of the weights divided by the sum of the volumes (sp. g. = w + w’ + w” , &c./v + v’ + v”, &c.). In the above example the sum of the volumes is 2 c.c. ; the weights (got by multiplying each volume by its corresponding sp. g.) are 1.4 gram and 1 gram. The sum of the weights divided by the sum of the volumes is 2.4/2 or 1.2.

The sp. g. of a mixture of 10 c.c. of a substance having a sp. g. of 1.2, with 15 c.c. of another having a sp. g. of 1.5 may be thus found:—

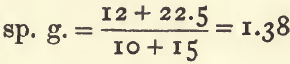
multiply each volume by its sp. g. to get its weight :

10 x 1.2 = 12
15 x 1.5 = 22.5

add these together (12 + 22.5 = 34.5) and divide by the sum of the volumes (10 + 15 = 25) :

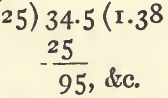
The sp. g. will be 1.38, provided the mixture is not accompanied by any change of volume.
The same formula will serve when the proportion of the ingredients is given by weight. A mixture of 4 parts by weight of galena (sp. g. 7.5) with 5 parts of blende (sp. g. 4) will have a sp. g. of 5.06 :

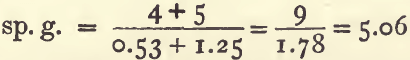
It is necessary in this case to calculate the volumes of the galena and of the blende, which is done by dividing the weights by the sp. gravities: thus, 4 divided by 7.5 gives 0.53 and 5 divided by 4 gives 1.25.

The converse problem is a little more difficult. Given the sp. g. of a mixture and of each of the two ingredients, the percentage by weight of the heavier ingredient may be ascertained by the following rule, which is best expressed as a formula. There are three sp. gravities given ; if the highest be written H, the lowest L and that of the mixture M, then :

Suppose a sample of tailings has a sp. g. of 3.0, and is made up of quartz (sp.g. 2.6) and pyrites (sp. g. 5.1): then the percentage of pyrites is 27 :

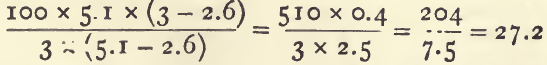
The same problem could be solved with the help of a little algebra by the rule already given, as thus : the sp. g. of a mixture equals the sum of the weights of the constituents divided by the sum of the volumes. Then 100 grams of the tailings with x per cent, of pyrites contain 100-x per cent, of quartz. The sum of
the weights is 100. The volume of the pyrites is x/5.1 and of the quartz 100 – x/2.6.

Then we have by the rule

If the percentage (P) and sp. g. (H) of one constituent and the sp. g. (M) of the mixture are known, the sp. g. of the other constituent may be calculated by the following formula, in which x is the required sp.g.:

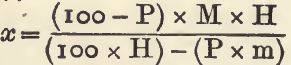
For example, “tailings” (sp. g. 3.0) containing 27.2 per cent, of pyrites (sp. g. 5.1) will contain (100-27.2), 72.8 per cent, of earthy matter having a mean sp. g. of x:

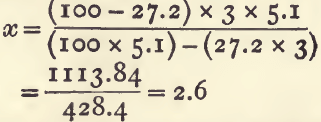
The differences in sp. g. corresponding to differences in strength have been carefully determined and tabulated in the case of the stronger acids and of many other liquids. Such tables are given at the end of this book.

To Calculate the Weight of a Measured Volume of Mineral or Rock.—Multiply the cubic feet by 62.4 and then multiply by the sp. g. of the stuff, the answer gives the weight in pounds. For example, 100 cubic feet of quartz weighs 100 x 62.4 x 2.6 = 16,224 lbs. The weight of any mass of mineral of known extent and sp. g. is ascertained in this way.

The following table gives the specific gravities of some of the commoner minerals.