Table of Contents
Although the model has been tested against only a limited amount of data the results shown in Figure 6 suggest that the model can be used to predict the flotation of fine particles in a column. The major advantage of the model is its ability to independently examine the influence of operational parameters on the performance of the flotation column. Several of the more significant of these parameters may be examined in further detail in the following discussion.
Effect of Hydrophobicity
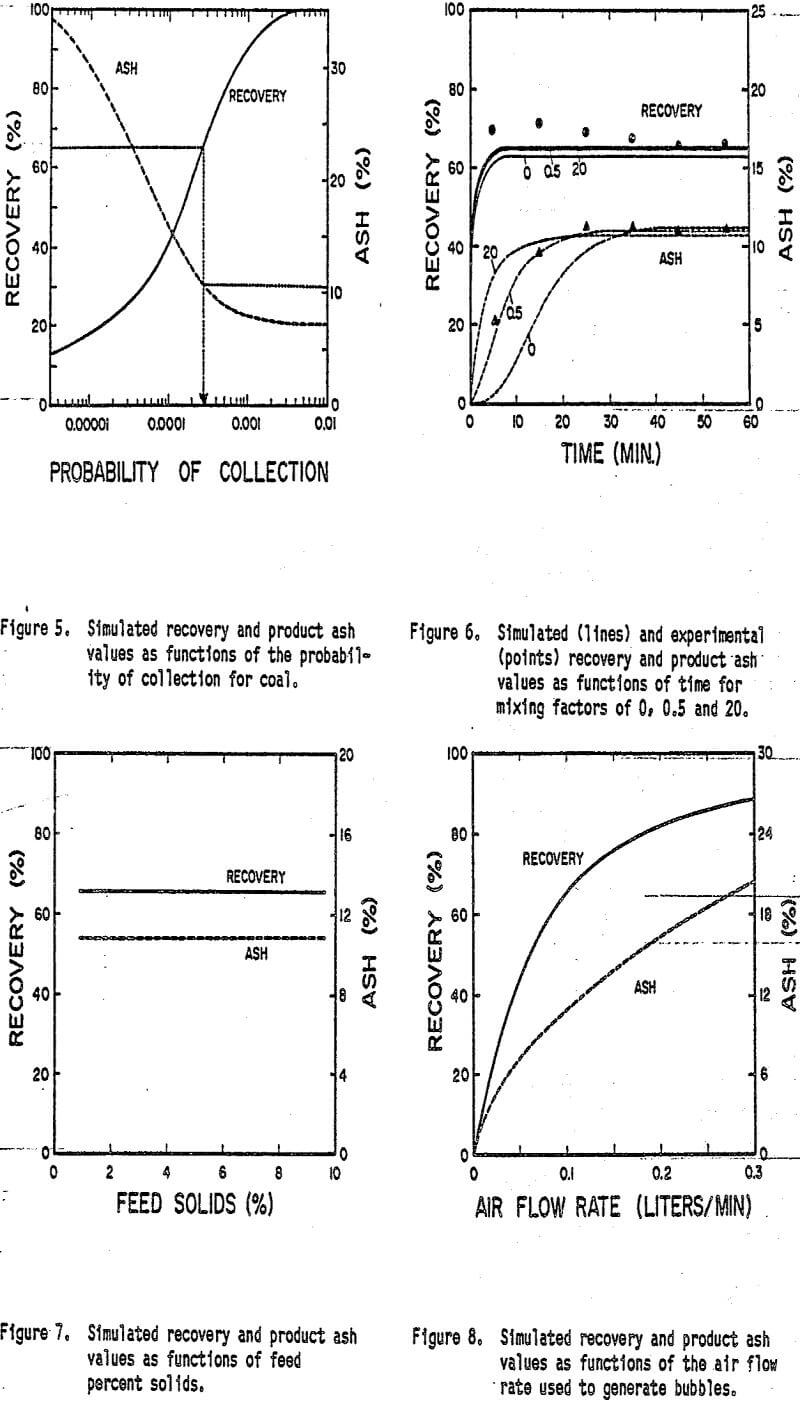
Given that bubble and particle sizes are constant an increase in the collection probability (P) of the coal reflects an increase in hydrophobicity. As shown previously in Figure 5, an increase in P (or hydrophobicity) increases both the recovery and ash rejection. This justifies the use of collectors such as kerosene or diesel fuel for coal flotation. However the extent of these improvements is constrained by particle entrapment and the upper limit of hydrophobicity attainable. In most cases other methods will be required in order to obtain improved performance.
Effect of Feed Percent Solids
As shown in Figure 7 the model predicts no change in the recovery of coal or rejection of ash when the feed percent solids is changed. However coal flotation experiments conducted as a function of percent solids have in some cases resulted in a significant change in the product ash content. The reason for this apparent discrepancy may be attributed to the fact that while the model assumes that a change in percent solids has no influence on the other operational parameters in actual experiments it may substantially alter other flotation variables such as reagent concentrations froth film thickness etc. Nevertheless, it may be possible that columns can be operated at a higher percent solids than conventional flotation cells.
Effect of Air Flow Rates
It is well known that the recovery of particles can be increased by using a higher flow rate of air through the flotation cell. However this procedure also tends to result in a higher product ash content. Figure 8 shows the results of simulations in which the air flow rate has been Increased while maintaining all other factors constant. The observed improvement in recovery is caused by an increase in the number of bubbles available for collision in the cell. For a fixed froth film thickness the increased number of bubbles also results in a rapid rise in water recovery which increases the flow of entrained ash into the product. Therefore as expected increasing the air flow increases recovery but adversely affects the product ash content.
Effect of Froth Film Thickness
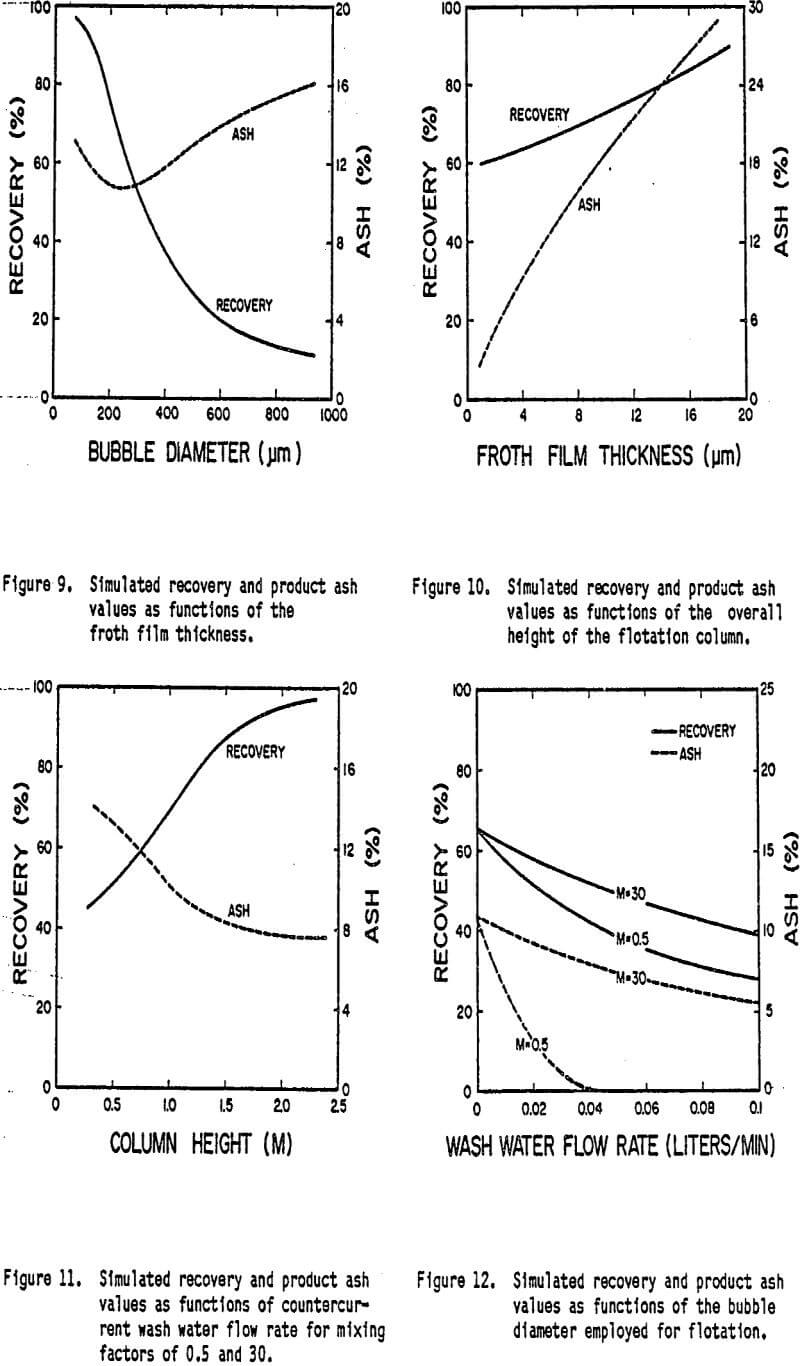
Figure 9 demonstrates the effect of changing the value of the froth film thickness (F) on the recovery and product ash content. As the froth becomes dryer (F decreases) the proportion of feed water reporting to the product is reduced. A direct result of the decrease in the water recovery rate is a corresponding decrease in the rate of recovery of entrained ash. Therefore the ash content of the product decreases with decreasing froth film thickness. Since coal and ash can both be entrained into the froth a decrease in coal recovery is also observed as the froth film thickness is decreased.
Effect of Column Height
A primary parameter in the design of column flotation is the height of the column. In order to study the effect of column height more closely a series of simulations were run in which the total height of the column was varied. During the simulations the feed point to the cell was maintained at a fixed distance from the top of the column. The results of the simulations (Figure 10) demonstrate the dramatic influence that column height has on the overall performance of the flotation column. As the column height is increased the retention time of particles is increased correspondingly for a given feed rate. Since recovery is a function of particle retention time a longer column results in a higher recovery. Although bubble loading was not considered in this model recovery would be limited in an actual case by the extent of bubble loading.
The drop in the ash content as-column height is increased is due to the fact that the recovery rate of coal increases while the recovery rate of ash remains the same. For the column studied in the present work a column height of at least 2 meters should have been employed in order to achieve the best possible results. Note however that as with previous examples improvements in the product ash content begin to diminish upon reaching the maximum recovery of the coal. Once again the extent of ash rejection is limited by entrapment.
Effect of Wash Water
One of the primary advantages claimed by the creators of column flotation is the ability to minimize the entrapment of fine gangue particles by using a counterecurrent flow of wash water. Figure 11 shows the results of two sets of simulations. In which this possibility has been investigated. In the first series of simulations the normal mixing level (M = 0.5) has been employed. As shown the wash water has a dramatic effect on the product ash content essentially eliminating ash recovery at flows greater than about 0.04 liters/min. However a significant drop in the recovery of coal also occurs. Two reasons can be cited for the decrease in coal recovery. First, since both the unattached coal and ash particles can be recovered by entrapment, there may be a significant loss of recovery of unattached particles when entrapment is reduced. Secondly, the increased flow of water tends to increase the percentage of bubbles which are washed out the bottom of the column, thus resulting in a loss of coal recovery.
Another series of simulations was performed under identical conditions, but using a higher degree of mixing (M=30). As shown in Figure 11, the effectiveness of the wash water stream decreases when the intensity of mixing is increased. Since a significant portion of unattached particles are still recovered by entrapment, the effect of the wash water on the coal recovery is not as large.
Effect of Bubble Size
A great deal of interest has been shown lately regarding the effect of bubble size on the recovery of fine particles. Theoretical and experimental results have been reported which suggest that the recovery of fine coal particles increases rapidly with decreasing bubble size (Bennett et al., 1958; Yoon, 1982). Evidence has also been presented indicating that selectivity increases with decreasing bubble size (Yoon, 1984). In order to more closely examine the effect of bubble size on flotation response, a series of model simulations have been carried out as a function of bubble diameter. The appropriate values of the probability of collection for each bubble size have been determined using a theoretical analysis described by Luttrell (1986).
The simulated results shown in Figure 12 demonstrate the dramatic increase in coal recovery as bubble size is reduced. This trend occurs as a result of the increasing probability of collection of coal with decreasing bubble size. It can also be seen that the ash content of the product decreases with decreasing bubble size until a bubble diameter of approximately 250 microns is reached. Below this value, the ash content-tends to increase with decreasing bubble size. This increase in ash content for very small bubble sizes has been observed experimentally (Luttrell, 1986), and has been explained by the Increase in water recovery (i.e., entrapment) with decreasing bubble size.
Although the simulations suggest that maximum ash rejection is obtained for a particular bubble size, the benefits derived from the increase in recovery obtained with very small bubbles may outweigh the corresponding small increase in ash. Without using small bubbles, the height of the column necessary to obtain high recoveries of ultrafine particles would most likely be prohibitive. Furthermore, the real advantage of using small bubbles may be found in the fact that the degree of mixing can be reduced. As shown in Figure 12, the wash water becomes less effective as the column becomes more mixed. The use of small bubbles creates conditions closer to plug-flow, which is an essential requirement for the column to operate efficiently.
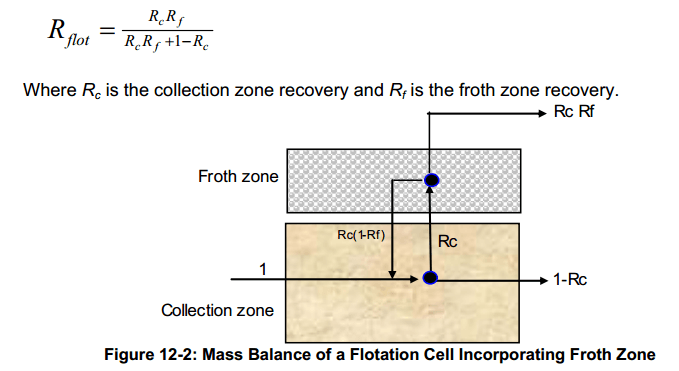
With the advent of column flotation in the early 1980s, research funds were made available to study column flotation. Models began to evolve to describe the column cell froth zone, and these were later applied flotation cells in general. Lynch (1981) associated the recovery of hydrophilic particles with water recovery to the concentrate.
Warren (1983) improved the entrainment concept by applying entrainment to hydrophobic particles as well. The first compartmental models began to emerge, such as the approach of Finch and Dobby (1990) described by the familiar depiction shown in Figure 12-2.
The fractional recovery by flotation, Rflot, for the system in Figure 12-2 may be defined as:
Froth recoveries were rarely applied in laboratory test work interpretation, despite the warnings of Arbiter and Harris. Although some researches found little selectivity in froth recoveries (Vera, et al., 1999), others (i.e.Honaker, 2005) reported that weakly floatable mineral species had preferential detachment in the froth zone.
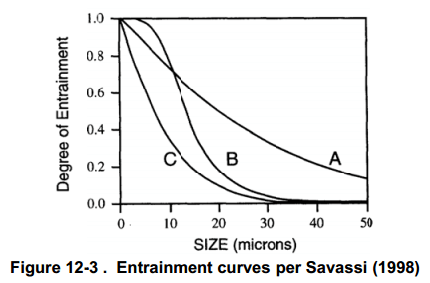
In the late 1990s and early 2000s, research into the froth zone behavior intensified. It has been recognized since at least 1976 that the rate of entrainment of particles into the concentrate is linearly proportional to the water recovery (Torne et al., 1976), yielding the well-known equation for degree of entrainment (D.E., shown here in the form published by Savassi (2005): 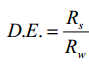
where Rs is the solids recovered to the concentrate by entrainment and Rw is the water recovery to the concentrate. Savassi made many measurements of the degree of entrainment and suggested three types of relationships: a high degree of entrainment (Curve A) with preferential drainage of coarse particles, an intermediate curve (B) for preferential drainage of coarse particles and curve C representing a low degree of entrainment. All three models predict that slime-sized particles will entrain into the
concentrate at approximately the same rate as water.
The incorporation of a froth zone model and entrainment effects into the interpretation of laboratory batch flotation processes was suggested by Vera et al. (2002). Dobby et al. (2002) reported the incorporation of entrainment recovery but made no mention of a froth zone recovery model for rate constant determination.
In parallel with the advancements in froth zone modeling, research into the fundamentals of the collection zone model were also progressing. Polat et al. (2000) expanded the concept of rate constant distribution by relating it to particle size. Dobby and Savassi (2005) proposed working with more abstract cumulative distribution functions, termed k-distributions, that are, at least initially, determined through particle size distribution measurements in the lab. Gorain et al. (1998) proposed a relationship between the bubble surface area flux through the collection zone (Sb) and the first order collection zone rate constant; Deglon et al. (1998) further developed the idea. Researchers began to express the rate constant as a linear function of Sb. There is some discussion on the precise nature of the relationship (for example, see Heiskanen 2000), but one such expression, proposed by Hernandez et al. (2003), relates the rate constant to the values of Sb and froth recovery:
k = PSbRf
where P is the “floatability factor,” which encompasses the particle size and hydrophobicity.
Given the findings summarized the above Equation, it should not be surprising that in recent years there has emerged an extensive body of research aimed at predicting the bubble surface area flux as a function of various chemical, mechanical, and metallurgical parameters.