G. Kuczynski and B. H. Alexander—This paper represents a most noteworthy attempt to evaluate experimentally the surface tension of a solid metal. Because of the great importance of such measurements, any proposed method should receive the closest scrutiny before the results can be considered reliable.
The writers think, however, that the experimental results are fairly reliable, but that there may be other methods of interpreting them depending upon what mechanism is assumed to be responsible for the shrinkage of the wires. The authors have assumed that the stress due to surface tension results in viscous flow. It should be made clear that it has never been demonstrated that viscous flow can occur in metal crystals even at very high temperatures. The experiments of Chalmers on tin, which are so frequently quoted as giving evidence of viscous flow at low stresses are by no means satisfactory. In his experiments, Chalmers found that only the initial rate of flow was approximately proportional to stress. He also found that the rate of flow varied markedly with time which, in his experiments, was less than 2 hr. Inasmuch as there is no proof of viscous flow in metals, and the authors have brought forth no conclusive evidence on this point, it may be worth while to investigate other possible mechanisms of material transport which would account for the shrinkage of the wires. The writers wish to point out that in these experiments the shrinkage of the wires can be adequately explained, according to a self diffusion mechanism. Thus, if we assume a concentration gradient for self diffusion which is a function of the radius of curvature of the wires, and assume that diffusion will occur so that the total surface area is decreased, we find the following expression for the self diffusion coefficient :
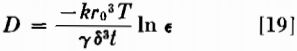
where k = Boltzmann constant
r0 = initial radius of the wire
T = absolute temperature
γ = surface energy
δ = interatomic spacing
t = time
ε = strain at zero applied stress
Eq 19 may be used to evaluate the self diffusion coefficient of copper, using the strain measurements obtained by the authors for zero stress as obtained by extrapolating their curves for 5 mil wires. By inserting a reasonable value for the surface energy (1500 ergs per cm²) we find:
![]()
The activation energy is of the correct order of magnitude, but the frequency coefficient is much too high, indicating that surface diffusion may be playing an important role. This discrepancy in the action constant is much smaller than the corresponding discrepancy obtained by the authors for the viscosity coefficient.
H. Udin (authors’ reply;—All of the test specimens were annealed at 1000°C for an hour or more before preliminary measurements were made. During this anneal the wires recrystallize, and the greatest part of grain growth takes place. Also, the knots sinter at the cross-over points. This does not in itself eliminate the possibility of end errors, although it greatly decreases their probable magnitude. It is still possible that some extension occurs due to creep in shear at the sintered points. If so, this effect would be quite independent of and superimposed on the normal shrinkage or extension of the wire itself.
Viscous flow in a polycrystalline metal may be either sliding of the grains upon their neighbors, or crystallographic slip (“recovery flow,” due to the continued removal of strain hardening by thermal agitation). Grain boundary sliding in general slows down with time, because the unevenness of the grain boundaries resists the continuation of the sliding movement; in the present case, however, the boundaries were nearly plane. On the other hand, they were also nearly perpendicular to the axis of tension, so that boundary sliding may not have played an important part; the main part of the deformation was probably by intracrystalline slip.
One can prove that the tendency to necking, which is typical of plastic deformation governed by a stress-strain curve of the usual type, is practically absent if the deformation obeys Newton’s law of viscosity. Yet it is difficult to see why cylindrical single crystals should always retain a circular cross-section during flow. If they flatten, the value of the surface energy derived from the measurement will be different from that obtained with the assumption of a circular cross-section, although the difference will amount only to a factor of order unity.

