A search of the literature reveals that no measurements have been made of the forces acting between a small solid particle whose surface is hydrophobic, and an air bubble to which the solid adheres, both immersed in water. Analyses have been made of the forces acting to support a greased solid on the surface of water, and the forces acting to cause a solid, whose surface is hydrophobic, to adhere to an air bubble in water. The latter analysis is often incomplete, however, because the internal pressure of the bubble has been neglected. It will be demonstrated that the internal gas pressure is not a negligible factor when dealing with bubbles of the size encountered in flotation.
A study of the forces acting between an air bubble attached to a large flat surface is informative. It must be borne in mind, however, that this is not the condition present in a flotation cell, where the particle is small compared to the size of the bubble. The bubble is allowed to spread to its maximum contact angle on a large flat surface in the first case, whereas in the second case, the spread of the bubble is limited to the surface of the small particle which is presented to the bubble.
Experimental Procedure: Briefly, the experimental procedure was as follows. A bubble of air was generated in distilled water. A rod of known diameter, one end of which was water repellent, was attached to this bubble. The weight of the rod was measured. The internal pressure of the bubble was measured with a manometer. The hydrostatic head from the surface of the water to the bottom of the rod was measured. The angle between the horizontal projection of the end of the rod and the tangent to the bubble at the circle of contact between rod and bubble was measured. This will be denoted as θ hereafter. The forces acting upward and downward, between rod and bubble were then evaluated.
In order to check the accuracy of the pressure measurements, La Place’s equation was used.
ΔP = γ(1/R1 + 1/R2)……………………………………………………………………..[1]
where ΔP = pressure differential across a gas liquid interface in dynes per cm² and γ = surface tension in dynes per cm, and R1 and R2 are the principal radii of curvature of the interface at the point where the pressure differential is measured, both expressed in centimeters.
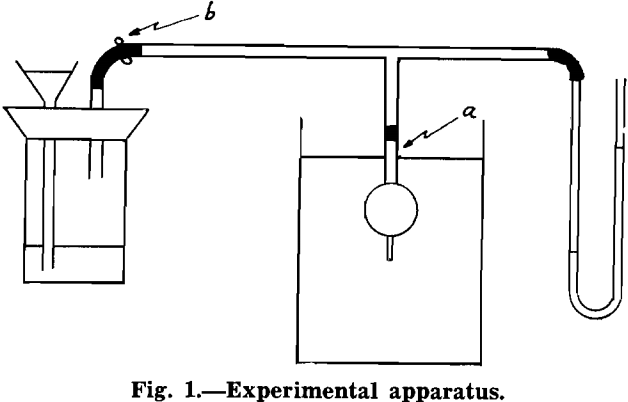
A bubble was generated in distilled water. No rod was attached to it. The radius of curvature of the bubble at its nadir was measured. The hydrostatic head from the surface of the water to the nadir of the bubble was measured. The difference in levels in the limbs of the manometer was measured. Acetone, rather than water, was used in the manometer because the difference in levels was greater than if water had been used, and also this liquid responded more quickly to pressure changes than did water, because of its lower surface tension. Since a differential manometer was used to measure internal pressure, atmospheric pressure was not taken into account in measuring hydrostatic head.
Attachment of Small Rods to Bubbles: In the first series of tests, glass rods of varying length and diameter were used. The ends of the rods were dipped into molten paraffin and cooled. This end was pressed against a clean glass slide in order to give a plane surface at the end of the rod.
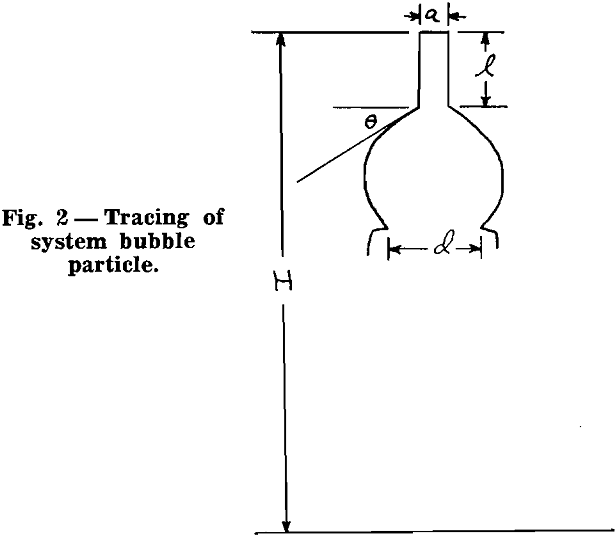
Now, the greater is the difference between maximum contact angle and static contact angle, the greater is the ability of the bubble particle system to withstand disruption. This difference is herein referred to as the flexibility of the system. For example, if the static contact angle for a given system is 50°, and if the maximum contact angle is 60°, the degree of flexibility is low, namely 10°, and such a system could not withstand disruptive forces to the extent that a system whose static contact angle is 20°.
Now this does not mean that only large bubbles are desirable in a flotation cell. Experience has shown that a large number of bubbles are desirable for best results. Thus, the greater the number of bubbles the greater is the number of particles attaching to them per unit of time, and hence the greater is the rate of flotation. For a given cell volume, and a given air intake per unit of time, the smaller the bubble, the greater the number of them.

