Table of Contents
Crushing has always been a major operation in the chemical and metallurgical industries, yet little is known about the theory of crushing, and today, the design of crushers is still based almost entirely on empirical knowledge and accumulated practical experience. In view of the increasing national need for the economic working of poorer grades of ores, the lack of a fundamental understanding of this unit operation hardly presents a satisfactory situation.
Fracture of Solids
This phase of the crushing problem is the most fundamental because it is concerned with the actual mechanism of fracture. The main problems in a study of the fracture process are concerned with the questions of why and how fracture occurs and why there is such a discrepancy between the actual and theoretical energies needed in a fracture process.
Since a mass of data has been accumulated on the fracture strength of materials, several investigators have attempted to correlate this data in the form of an equation. Glathart and Preston, Taylor, Poncelet, Machlin and Norwich, and Frederickson and Eyring have all considered this problem, and the final relationship has always been that the stress for fracture is proportional to the logarithm of time. Murgatroyd arrived at a very similar relationship by a different method.
Size Distribution of Crushed Material
The size distribution of crushed materials has been studied for many years but the information obtained was generally used as a measure of the surface area or the state of the final product and not as a means of studying the actual mechanism of crushing. Screen analyses run on crushed samples have established a definite relationship between the weight retained on a screen and the size of the screen opening. Schuhmann presents some of the latest work on this. The same relationship has been used by Bond in deriving his method of evaluating surface areas of crushed materials from a screen analysis.
Gaudin and his associates have used their data on size distribution to derive some hypotheses on crushing, making use of various postulates by Andreasen and Bennett, Brown, and Crone to synthesize size distribution curves which agree very well with experimental data. Epstein has used an idea similar to that of Bennett, et al, in his recent study of the size distribution of a crushed solid. From the experimental data which they obtained Gaudin and his associates made the amazing conclusions that “1—The size distribution of broken fragments made by a single fracture is such that the new surface on each grade is the same; and 2—Multiple fracturing results in a size distribution such that in the fine sizes, the surface per grade is the same in every grade; in coarse sizes the surface per grade decreases gradually with increasing size.” This is about the only work that attempts to make use of the size distribution of a crushed product as a key to the understanding of the fracture process.
Energy Input Vs. New Surface
Energy Measurement: Studies of the crushing process have been complicated by the fact that a valid measurement of the energy input to a crushing operation is difficult to measure. Several attacks are possible. One can try to measure, for example, the energy input to a commercial machine, the energy input to a bed of particles in a simple crushing device, the energy input to a single particle, or measure the difference in the total energy levels of the material before and after crushing. The last is the most basic but is difficult to perform today.
Surface Area Measurement: Although surface measurements made on fine materials by means of gas adsorption and the electron microscope are probably a close approach to the true value, these methods were not available until recently. The most common method of determining the surface area of particles has been the indirect one of obtaining a screen analysis and more or less arbitrarily assigning a shape factor to correct for the assumption that the particles were perfect spheres or cubes.
The most promising and most recent method for surface area determination is the gas adsorption method. Wooten and Brown have adopted the general adsorption method developed by Brunauer, Emmett, and Teller to the determination of small areas, and this has considerably increased the range of areas which can be measured. This method was used by Gaudin and Hukki and at the University of Minnesota in studies on the crushing of quartz.
All of the materials considered so far have been supposedly brittle materials. The crushing of a non-brittle but crystalline solid is now considered.
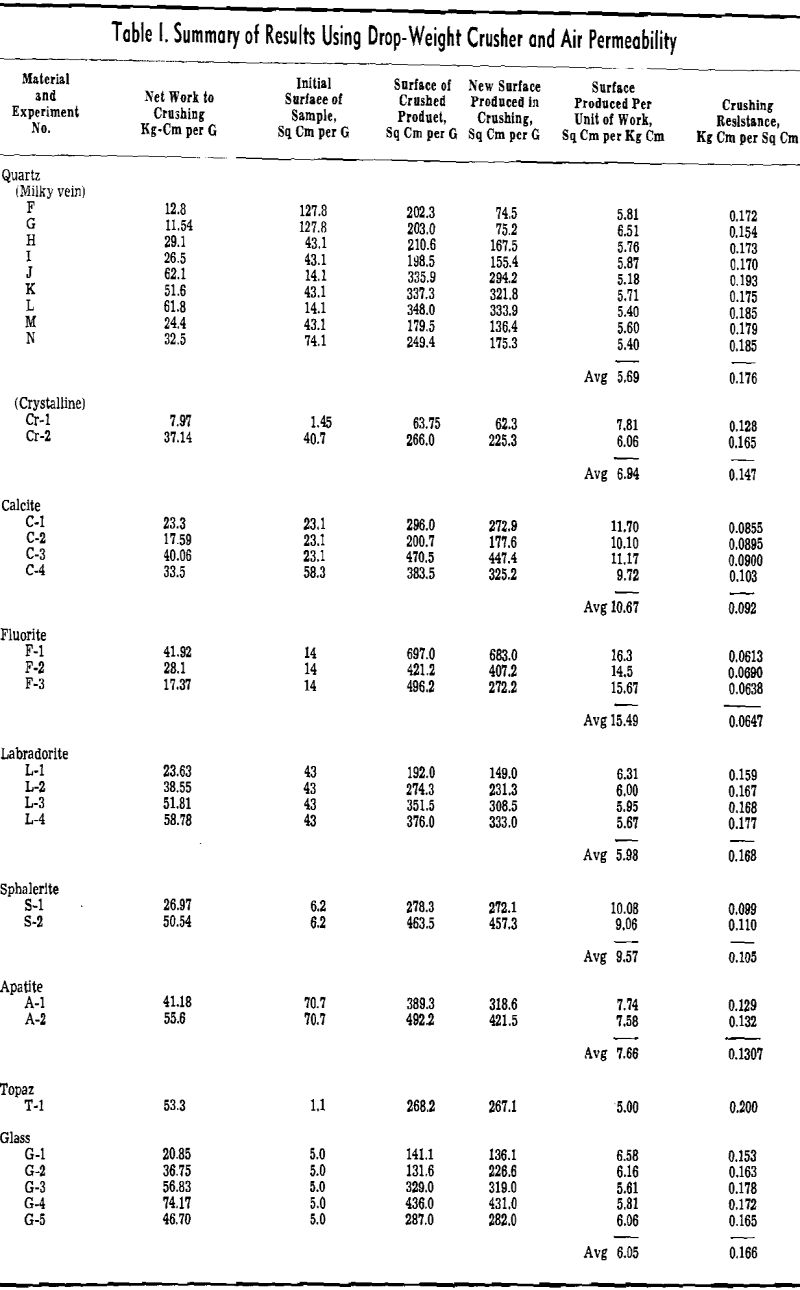
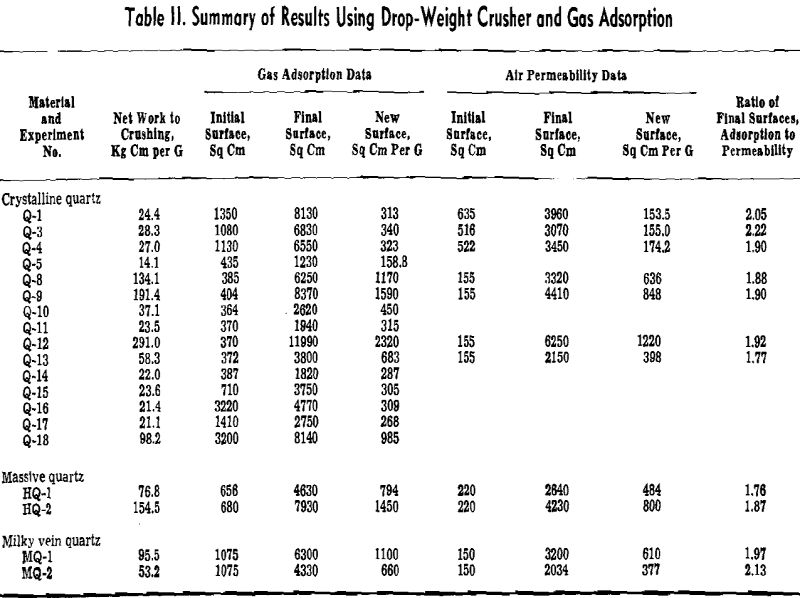
A series of experiments was conducted with 5 to 20-g samples of quartz in which the crushing was accomplished with the drop-weight crusher and the areas were measured by the gas adsorption method and, in some cases, also by the air permeability method.
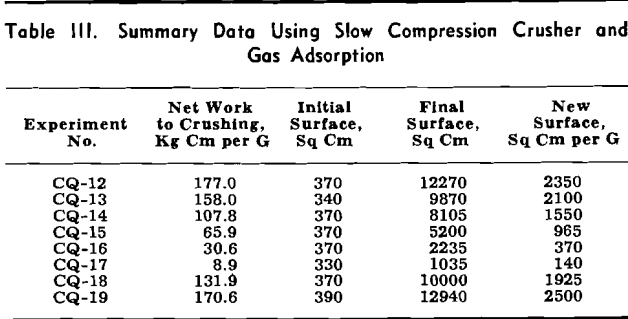
Slow Compression Crusher: In an attempt to obtain a more accurate measure of the actual energy input to the material, a series of experiments was conducted in which the crushing of quartz was accomplished by slow compression in a mortar between the platens of a small hydraulic press.
Since the return of the elastic energy imparted to the crushing assembly during compression could not be measured after fracture occurred as with the multiple particles, a correction was made for this.
With only 1 to 2 pct of the energy input for the crushing of multiple particles appearing as surface energy in the crushed product, it seems quite improbable that a constant relationship could occur over any appreciable range between the energy input and the new surface produced. The straight line relationships which have been found experimentally are believed to be the result of a statistical average for the large number of particles crushed.
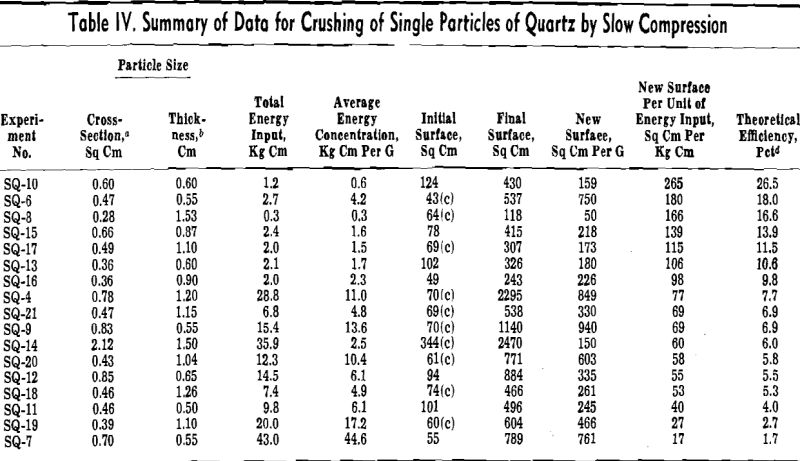
It is significant that in the single crystal experiments the amount of new surface formed per unit of energy input was always greater than in the multiple particle experiments. At the lower average energy concentrations this ratio was as high as 19 to 1. Although the data for the single crystal experiments are quite scattered and group themselves most frequently around an average energy concentration near 5 kg-cm per g, a relationship is shown between the new surface formed per unit of energy input and the average energy concentration at fracture. One explanation of this relationship makes use of the concept of a critical stress value to produce fracture.

