Comminution is an old art. Unfortunately the analysis of the unit operations has been handicapped by the lack of both theoretical and experimental information. Two types of information are needed, one an understanding of what happens when a particle breaks in a brittle manner; and two, an understanding of what happens when the daughter fragments pass through the mill.
Recently, successful theoretical attacks on the fracture of brittle solids have yielded significant results. New experimental techniques are yielding insight into the physical phenomenon occurring during brittle fracture. Many of the re-doubtable shiboliths of the last century are either being laid to rest or verified.
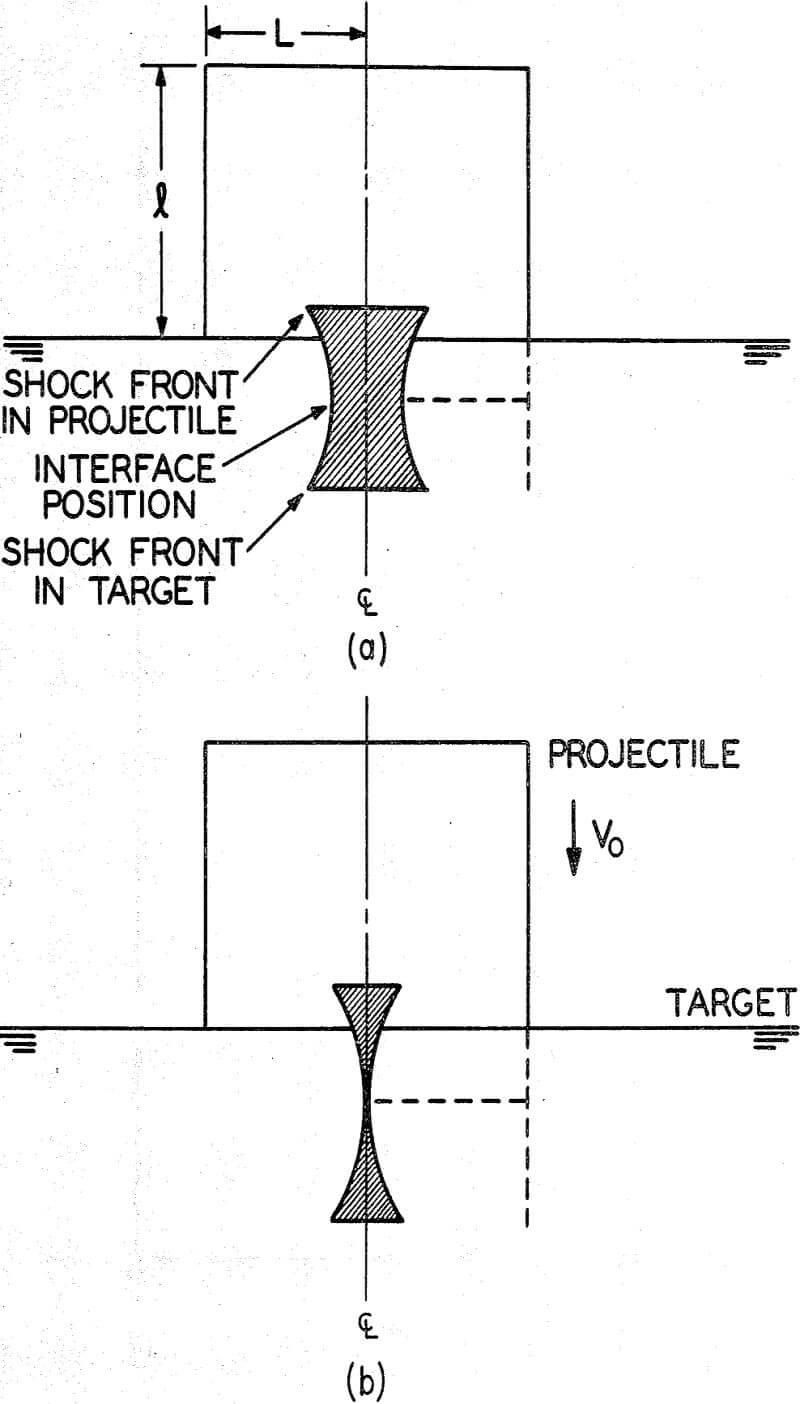
The problem with a shock wave is that, from its beginning to its decay into a compressive elastic wave we do not fully understand the dynamics. The shock wave proceeds into the target material as well as into the projectile material. The shock wave moves both perpendicularly into the target and the projectile. However a rarifaction wave originating at the edge of the material eats into the compressive shock wave, attenuating it.
Hypervelocity impacts are spectacular phenomenon. Material in the liquid state is ejected from the early crater at velocities exceeding that of the impacting projectile. Associated with the impact is an intense flash of light and electrical discharge. Reasonably good models for the intensity, position and speed of the shock wave have been established by a number of workers in the field.
Both models imply the crack density is a function of the compressive energy stored in the crystal prior to fracture. Furthermore, it is implied that the crack density or size reduction is the linear function of this energy. No reason is given for this linear relation. Many investigators agree with this assumption. It is reasonable to state that the crack density is a monotonically increasing function of the compressive energy stored in the lattice.
Hypervelocity comminution different from classical comminution because in hypervelocity impact the energies and pressures can be varied radically with respect to the breaking strength of the material. Furthermore it is known that the energy in the compressive elastic wave drops off with increasing distance from the point of impact. This too was a departure from classical comminution where the compressive energy is stored uniformly throughout the specimen.
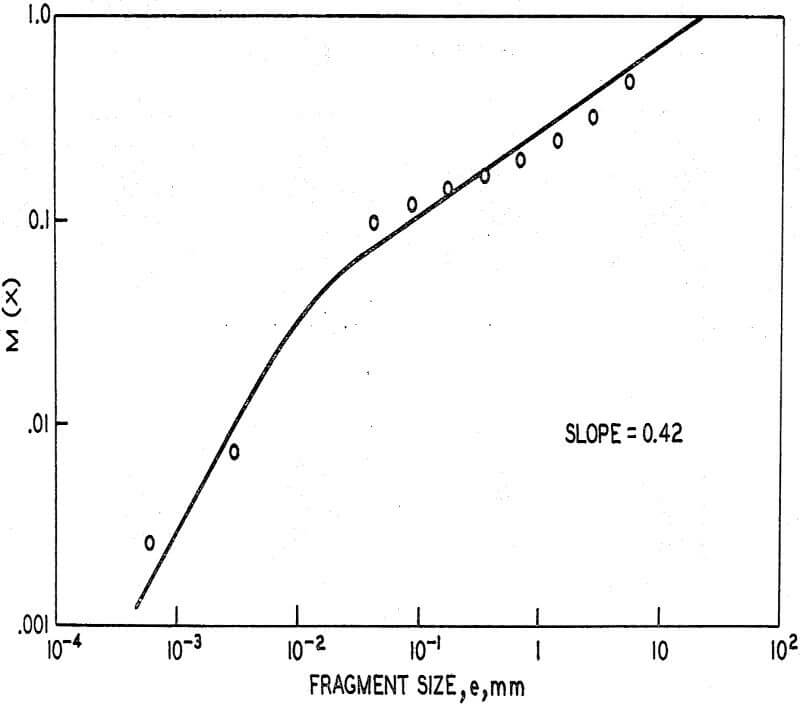
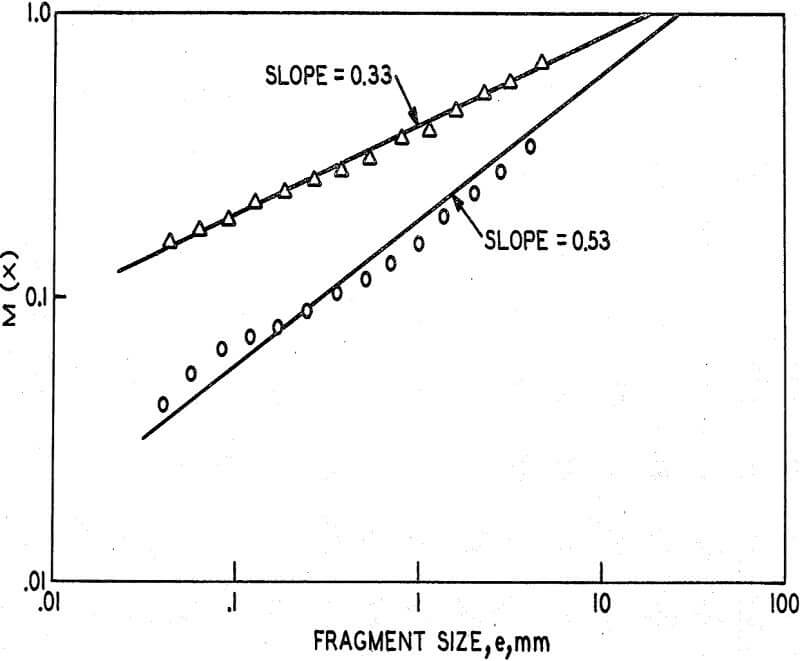
The experimental size distribution data of Gault, Shoemaker, and Moore, has a slope less than 1 in the upper size range. This curve, which appears to be a straight line, does not fit the curves predicted by either Gilvarry or Meloy.
Modern comminution theory does not predict the correct size distribution of the fragment from a hypervelocity impact event in brittle targets. A modification of the theory has been proposed. The modification states that degree of comminution – crack density – is directly proportional to the energy in the compressive wave as it passes through the specimen. Comminution stops when the energy in the wave falls below a minimum, characteristic of the material.
The theoretical size distribution predicted for single particles compressed uniformly is not the size distribution that will be observed in mills, because the compressive energy stored in the crystal lattice just before the breaking is not uniformly distributed. Most ore particles may be considered to be tetrahedral in shape before they are broken. The particle rests on a three point base and is broken by pressure applied to the highest point. The compressive pressure energy reaches a maximum at the top of the particle and falls off towards the base. Thus the size distribution will be more like that predicted for a hyperyelocity impact event. Specifically, in the larger sizes the curve will be straight and have a slope less than one. This may explain why experimental mill results show the flatter slopes in the upper size ranges.