A size-continuous breakage kinetics model is postulated and supported with industrial grinding mill data. It is shown that the kinetics parameters include the effects of possible classification at the mill discharge. The estimated parameters were then used in the kinetics model to simulate the behavior of a grinding mill in open and closed circuit operation. While material transport and kinetics are equally important in open loop operation, heavy recycle in a closed circuit make a detailed material transport model for grinding unnecessary. In effect, the mill can be considered as backmixed.
The PSD produced in a continuous grinding circuit can be described by the complex interaction between breakage kinetics and material transport (i.e., size-dependent residence time) in the mill. Closed-circuit recycle of hydrocyclone oversize particles complicates the interaction of these two factors. Due to the empirical formulation of breakage kinetics and classification functions, few generalizations can be made on the expected form of PSD from closed-circuit continuous mills.
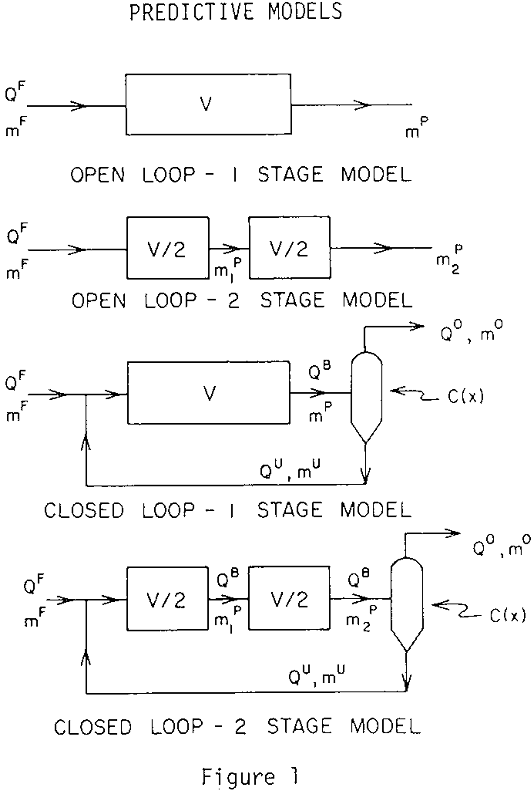
The kinetic theory of grinding has resulted in several types of model formulations, viz., various combinations of continuous and discreet formulation in the particle size and time domains. Though size discretization offers several computational conveniences, size-continuous models offer the hope of formulation with fewer parameters if sufficiently clever model forms are chosen.
Practically speaking, residence time distributions (R-T-D) in real mills can be modeled more effectively by considering deviations from the backmixed, rather than plug-flow, idealization. The use of ODE’s, rather than the PDE’s, is an enormous advantage for models of the former type. Distributed models are virtually precluded when used for dynamic control purposes.
Such models can simulate a non-ideal backmixed grinding stage which might otherwise require a set of N backmixed equations to describe. The mathematical simplification of this non-capacitive size-dependent removal function approach is obvious. Although steady-state first order kinetics systems can be modeled exactly with this approach, the phase response in a dynamic system might not be modeled exactly.
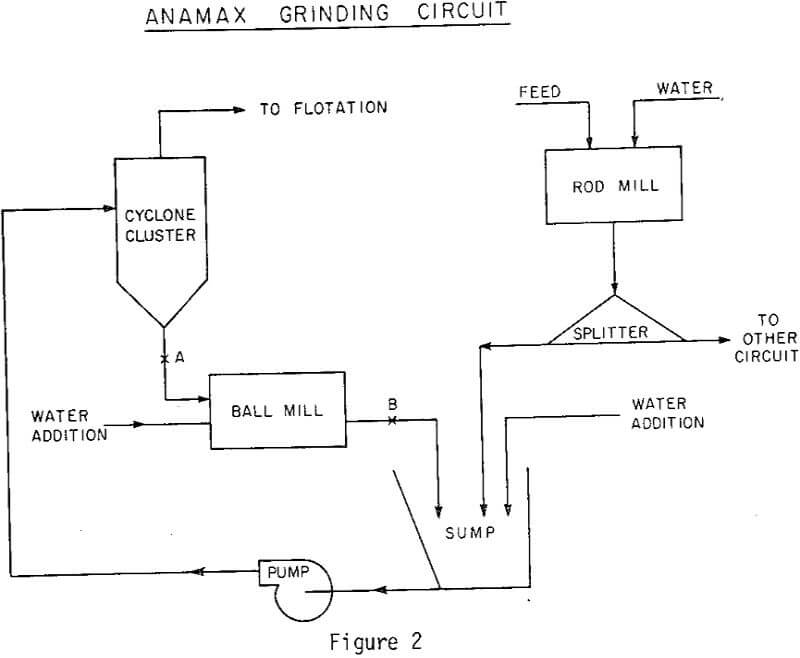
Input/output PSD data were taken from a closed-circuit industrial ball mill at the Twin Buttes operations of the ANAMAX Mining Company.
The difference in open-circuit PSD is somewhat more pronounced at the longer retention time. The overall residence time distribution in the closed-circuit mill is totally dominated by the hydrocyclone recycle. Thus, a heavily recycled system becomes in effect a backmixed system and local material transport (through the mill) is insignificant in shaping the overall R-T-D.
The PSD models illustrated in this paper indicate that one technique for modeling the material flow (size-dependent R-T-D) is to assume classified discharge from a one-stage mixed particle slurry. Such classification is indistinguishable from the size-dependence of the breakage kinetics when steady-state open-circuit operation is considered. PSD calculations in the closed-circuit mode indicate the relative insignificance of the ball mill material transport model, whatever form it might be expressed as.