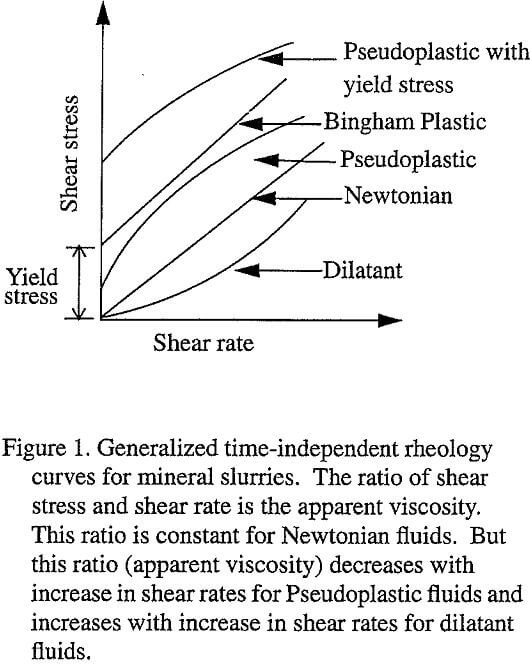
Mineral suspensions show Newtonian flow properties at lower solid concentration, but change into non-Newtonian regime as the solids content is increased. For Newtonian fluids viscosity is independent of shear rate, but for non-Newtonian fluids it varies with rate of shear. Therefore, measurement of viscosity at a shear rate, different from the process will be futile unless the slurry is Newtonian. This is especially true for hydrocyclone operation, where the rate of shear is different at different points within the hydrocyclone. In this case, it is very important to determine the flow type of the suspension before attempting to establish any correlation between viscosity and process efficiency.
In order to demonstrate this, the shear rate within a hydrocyclone can be calculated from its different velocity components and radius, as described below:
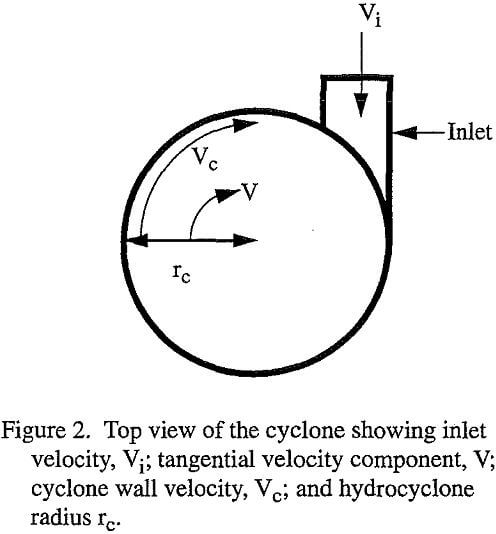
Rate of shear, S can be obtained as:
S = dV/dr
where, V = tangential velocity and r = radius.
From conservation of angular momentum:
Vrn = constant
Where, n is an experimentally-determined constant (0.6 < n < 0.9)
For a particular test with silica slurry with a hydrocyclone of radius, rc = 4″, the inlet velocity, Vi was measured to be 5.0 – 5.5 ft/sec (from flowmeter measurements). For this test maximum shear rate inside the hydrocyclone can be calculated by assuming α = 0.45, n = 0.8, and occurrence of maximum tangential velocity at r = rc/8 . By substituting these values in the expression for shear rate, the maximum shear rate (at r = rc/8) was obtained to be 456 sec-¹. For example, the viscosity readings obtained by a Brookfield viscometer operating at shear rates below 74 sec-¹ cannot be used to determine the viscosity effects inside the hydrocyclone where the shear rate is as high as 456 sec-¹, unless the slurry is known to be Newtonian. Therefore, before using any model involving viscosity, one must insure that the fluid is Newtonian in its flow behavior.
Methods and Materials
Viscosity of a Newtonian fluid is not affected by shear rates, but for non-Newtonian fluids viscosity changes with changes in shear rate. Thus, by measuring the viscosity at two different shear rates sufficiently apart from each other and comparing the two values, the fluid can be designated as Newtonian if both the viscosities are similar, and non-Newtonian if the viscosities are different. Based on this concept, a new system was developed to determine the flow regimes of mineral slurries.
A Brookfield viscometer (DV-I model) was used to measure apparent viscosity at low shear rates. Two different spindles were used in this study for dilute and dense suspensions. The UL adaptor spindle was used for suspensions with a viscosity less than 10 centipoise and the LV 1 spindle was used for samples with viscosities above 10 centipoise. The UL adaptor consists of a cylindrical spindle and a tube which houses the spindle. The sample was placed in the annular space between the spindle and the tube for measuring its viscosity.
The Nametre viscometer consisted of a spherical probe, which oscillates along a vertical shaft at its resonant frequency of 750 Hz and a constant amplitude of 1 micron. This viscometer was selected because it operated at a much higher shear rate than the Brookfield viscometer and could measure viscosity as low as 1 centipoise. When immersed in a fluid, the probe created a shear wave in it.

